In probability theory, a sample space is the set of all possible outcomes of a random experiment or process. It is denoted by the symbol S and is a fundamental concept that helps to define probabilities and perform statistical analyses.
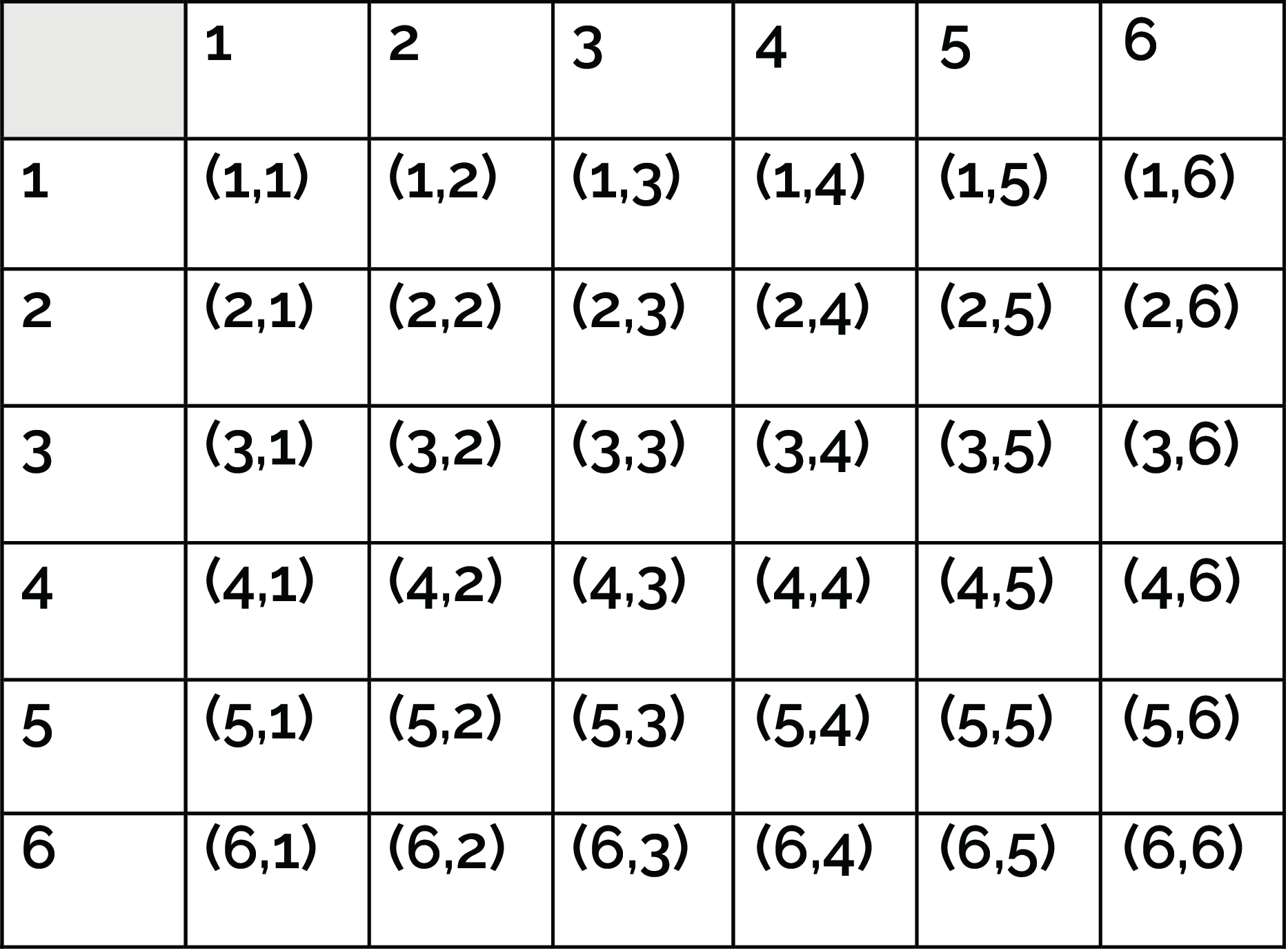
For example, suppose we are rolling a six-sided die. The sample space for this experiment would be {1, 2, 3, 4, 5, 6}, since these are the only possible outcomes. Each outcome is called an element or a point in the sample space.
In general, the sample space can be either finite, countably infinite, or uncountably infinite, depending on the nature of the experiment. For instance, if we are flipping a coin twice, the sample space would be {HH, HT, TH, TT}, which has four elements. If we are measuring the height of students in a class, the sample space would be an interval of real numbers, which is uncountably infinite.
Understanding the sample space is crucial for calculating probabilities and making statistical inferences. The events of interest are subsets of the sample space, and the probability of an event is defined as the proportion of outcomes in the sample space that correspond to that event.
What is Required Sample space
In probability and statistics, a sample space is the set of all possible outcomes of a random experiment or process. It is important to define the sample space when we are working with probabilities or statistics because it helps us to identify the possible outcomes of an experiment, and therefore, determine the likelihood of a particular event occurring.
The concept of a sample space is closely related to the concept of events. An event is a subset of the sample space, and it represents a particular outcome or set of outcomes that we are interested in. For example, if we are flipping a coin, the sample space is {heads, tails}, and we might be interested in the event that the coin lands heads up.
In some cases, the sample space may be infinite or uncountable. For example, if we are measuring the height of people, the sample space would be the set of all possible heights, which is an uncountable set. In such cases, we may need to use advanced mathematical tools to calculate probabilities and make statistical inferences.
Overall, understanding the sample space is essential in probability and statistics because it allows us to define events and calculate probabilities. By carefully defining the sample space, we can ensure that our analysis is both accurate and relevant to the problem at hand.
Who is Required Sample space
“Required Probability and Statistics Sample Space” is not a person, but rather a concept in probability theory and statistics. The sample space is a set of all possible outcomes of a random experiment or process. It is a fundamental concept in probability theory and is used to define events and calculate probabilities.
The sample space is important in many areas of science, including physics, biology, finance, and engineering, as it helps to determine the likelihood of certain events occurring. For example, in finance, sample spaces can be used to estimate the probability of certain market trends, while in biology, sample spaces can be used to predict the likelihood of a particular genetic outcome.
Overall, the concept of the sample space is important for anyone studying probability theory or statistics, including mathematicians, statisticians, scientists, and researchers. It is an essential tool for understanding the probabilities of various outcomes and making statistical inferences based on data.
When is Required Sample space
The concept of the sample space is required whenever we are working with probabilities or statistics. It is a fundamental concept in probability theory and statistics, and it is used to define the possible outcomes of a random experiment or process.
The sample space is used in a wide range of applications, from physics to finance, and it helps us to identify the possible outcomes of an experiment or event. For example, in finance, sample spaces can be used to estimate the probability of certain market trends, while in physics, sample spaces can be used to predict the likelihood of certain outcomes in quantum mechanics.
Whenever we want to make statistical inferences or estimate the probability of certain events occurring, we need to define the sample space. By defining the sample space, we can ensure that our analysis is both accurate and relevant to the problem at hand.
Overall, the concept of the sample space is required in many different contexts whenever we are working with probabilities or statistics. It is a fundamental tool for understanding the likelihood of various outcomes and making informed decisions based on data.
Where is Required Sample space
The concept of the sample space is not located in any specific physical location, as it is a fundamental concept in probability theory and statistics that is used in many different fields and applications.
The sample space is a mathematical abstraction that represents the set of all possible outcomes of a random experiment or process. It is used to define events and calculate probabilities, and it is a critical tool for understanding the likelihood of various outcomes and making informed decisions based on data.
The sample space can be used in many different contexts, from physics to finance, and it is an essential concept for anyone studying probability theory or statistics. It is not physically located in any one place, but rather it is a fundamental concept that is used in many different fields and applications around the world.
How is Required Sample space
The sample space in probability theory and statistics is defined as the set of all possible outcomes of a random experiment or process. The sample space is denoted by the symbol S and it is a fundamental concept that helps us to define events and calculate probabilities.
To illustrate how the sample space is used, consider the following example: if we are flipping a coin, the sample space is {heads, tails}, since these are the only two possible outcomes. Similarly, if we are rolling a six-sided die, the sample space is {1, 2, 3, 4, 5, 6}.
Once we have defined the sample space, we can define events as subsets of the sample space. For example, if we are flipping a coin and we are interested in the event that the coin lands heads up, then the event is {heads}, which is a subset of the sample space {heads, tails}.
We can use the sample space to calculate probabilities by counting the number of outcomes in the event of interest and dividing by the total number of outcomes in the sample space. For example, the probability of getting heads when flipping a coin is 1/2, since there is one outcome in the event of interest and two possible outcomes in the sample space.
In summary, the sample space is a fundamental concept in probability theory and statistics that helps us to define events and calculate probabilities. By carefully defining the sample space, we can ensure that our analysis is both accurate and relevant to the problem at hand.
Case Study on Sample space
Case Study: Flipping a Coin
Suppose we are interested in the probability of flipping a fair coin and getting heads. We can use the concept of the sample space to calculate this probability.
The sample space for flipping a coin consists of two possible outcomes: heads and tails. So we can define the sample space as S = {heads, tails}. The event we are interested in is getting heads, which we can denote as E = {heads}.
To calculate the probability of getting heads, we can use the formula:
P(E) = Number of outcomes in event E / Total number of possible outcomes
In this case, the number of outcomes in event E is 1 (since there is only one way to get heads), and the total number of possible outcomes is 2 (since there are two possible outcomes: heads and tails). Therefore, the probability of getting heads is:
P(E) = 1/2
This means that if we were to flip a coin many times, we would expect to get heads approximately half of the time.
Now suppose we are interested in the probability of flipping a coin three times and getting two heads and one tail. In this case, the sample space consists of all possible outcomes of flipping a coin three times, which can be represented as:
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
There are eight possible outcomes in the sample space. The event we are interested in is getting two heads and one tail, which can occur in three ways:
E = {HHT, HTH, THH}
Therefore, the probability of getting two heads and one tail is:
P(E) = Number of outcomes in event E / Total number of possible outcomes P(E) = 3/8
This means that if we were to flip a coin three times, we would expect to get two heads and one tail approximately 37.5% of the time.
In summary, the concept of the sample space is a fundamental tool in probability theory and statistics that helps us to define events and calculate probabilities. By carefully defining the sample space, we can ensure that our analysis is both accurate and relevant to the problem at hand.
White paper on Sample space
Introduction Probability theory and statistics are important mathematical disciplines that are used to model and analyze uncertainty and variation. One of the fundamental concepts in probability theory and statistics is the sample space. The sample space is a set that contains all possible outcomes of a random experiment or process. It is an essential tool for defining events and calculating probabilities, and it is used in a wide range of fields and applications, from physics to finance. In this white paper, we will discuss the concept of the sample space, its properties, and its applications in probability theory and statistics.
Defining the Sample Space The sample space is defined as the set of all possible outcomes of a random experiment or process. It is denoted by the symbol S and is a fundamental concept in probability theory and statistics. For example, if we are rolling a six-sided die, the sample space is {1, 2, 3, 4, 5, 6}, since these are the only possible outcomes. Similarly, if we are flipping a coin, the sample space is {heads, tails}.
Defining Events Once we have defined the sample space, we can define events as subsets of the sample space. An event is a collection of outcomes that we are interested in studying. For example, if we are flipping a coin and we are interested in the event that the coin lands heads up, then the event is {heads}, which is a subset of the sample space {heads, tails}.
Calculating Probabilities We can use the sample space to calculate probabilities by counting the number of outcomes in the event of interest and dividing by the total number of outcomes in the sample space. For example, the probability of getting heads when flipping a coin is 1/2, since there is one outcome in the event of interest and two possible outcomes in the sample space.
Properties of the Sample Space The sample space has several important properties that are worth noting. First, the sample space is exhaustive, meaning that it contains all possible outcomes of a random experiment or process. Second, the sample space is mutually exclusive, meaning that each outcome in the sample space is distinct and cannot occur simultaneously with any other outcome. Third, the sample space is collectively exhaustive, meaning that the union of all events in the sample space is equal to the sample space itself.
Applications of the Sample Space The sample space is a fundamental tool in probability theory and statistics and is used in a wide range of applications. For example, in physics, the sample space can be used to model the possible outcomes of an experiment, such as measuring the position of a particle. In finance, the sample space can be used to model the possible returns of an investment, such as a stock or a bond. In epidemiology, the sample space can be used to model the possible outcomes of a disease outbreak, such as the number of people who become infected.
Conclusion The sample space is a fundamental concept in probability theory and statistics that is used to define events and calculate probabilities. By carefully defining the sample space, we can ensure that our analysis is both accurate and relevant to the problem at hand. The sample space has several important properties, such as being exhaustive, mutually exclusive, and collectively exhaustive, which make it a useful tool for modeling uncertainty and variation in many different fields and applications.