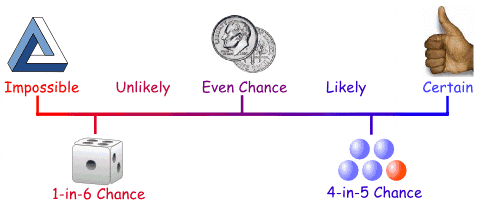
In probability theory, an impossible event is an event that cannot occur. It is a subset of the sample space that has zero probability of occurring. For example, if you roll a fair six-sided die, the event of getting a 7 is impossible, since the highest possible outcome is 6. Similarly, the event of flipping a coin and it landing both heads up and tails up at the same time is impossible.
Formally, if E is an event, and P(E) denotes the probability of event E, then an impossible event is defined as an event for which P(E) = 0.
It’s worth noting that just because an event has a probability of 0 does not necessarily mean it is impossible. For example, the event of rolling a 3.5 on a fair six-sided die has a probability of 0, but it is not impossible in a theoretical sense (although it is impossible in a practical sense).
What is Required Different types of events (Impossible)
In probability theory, events can be classified into different types based on their probability of occurrence. One such type is impossible events.
An impossible event is an event that cannot occur. It is a subset of the sample space that has zero probability of occurring. For example, if you roll a fair six-sided die, the event of getting a 7 is impossible, since the highest possible outcome is 6. Similarly, the event of flipping a coin and it landing both heads up and tails up at the same time is impossible.
Formally, if E is an event, and P(E) denotes the probability of event E, then an impossible event is defined as an event for which P(E) = 0.
It’s important to note that an event with a probability of 0 is not necessarily impossible. For example, the event of rolling a 3.5 on a fair six-sided die has a probability of 0, but it is not impossible in a theoretical sense (although it is impossible in a practical sense).
Who is Required Different types of events (Impossible)
“Required Probability and Statistics Different types of events (Impossible)” is not a person, but rather a topic or concept in the field of probability and statistics. It refers to the classification of events into different types based on their probability of occurrence, including the concept of impossible events which have a probability of zero and cannot occur. This is an important concept in probability theory and is studied in many different areas, including in fields such as finance, engineering, and science, where probabilistic models are used to describe and analyze various phenomena.
When is Required Different types of events (Impossible)
The topic of “Probability and Statistics Different types of events (Impossible)” is relevant whenever one is working with probability theory, which is a branch of mathematics that deals with the study of random events and their properties. In many real-world situations, it is important to understand the different types of events that can occur, including impossible events, in order to make informed decisions and predictions. This is relevant in many fields, including finance, engineering, science, and many others.
For example, in the financial industry, probabilities are often used to estimate the likelihood of certain events occurring, such as changes in stock prices or interest rates. Similarly, in engineering, probabilities are used to estimate the likelihood of failure of a particular system or component. In science, probabilities are used to describe and analyze the results of experiments and observations, and to make predictions about future events.
Overall, the study of different types of events in probability theory, including impossible events, is a fundamental part of understanding and analyzing probabilistic phenomena in a wide range of fields.
Where is Required Different types of events (Impossible)
The concept of “Probability and Statistics Different types of events (Impossible)” can be applied and studied in many different settings and fields, wherever probability theory is relevant. This includes:
- Mathematics: Probability theory is a branch of mathematics and the study of different types of events, including impossible events, is fundamental to understanding probability theory.
- Finance: Probability theory is used in finance to model risk and to estimate the likelihood of different financial outcomes. Understanding the different types of events, including impossible events, is important in this context.
- Science: Probability theory is used in many branches of science, including physics, biology, and chemistry. The study of different types of events is important in analyzing experimental results and making predictions about future events.
- Engineering: Probability theory is used in engineering to model and analyze complex systems, and to estimate the probability of system failure. Understanding the different types of events, including impossible events, is important in this context.
- Business: Probability theory is used in business to analyze data and make informed decisions. Understanding the different types of events, including impossible events, is important in this context as well.
Overall, the study and application of different types of events in probability theory, including impossible events, is relevant in many different fields and settings.
How is Required Different types of events (Impossible)
The concept of “Probability and Statistics Different types of events (Impossible)” is a fundamental aspect of probability theory. In probability theory, events can be classified into different types based on their likelihood or probability of occurrence. One such type is the impossible event, which is a subset of the sample space that cannot occur. An impossible event has a probability of zero.
The concept of impossible events is important in probability theory because it allows us to differentiate between events that can occur and events that cannot occur. This helps us to make more accurate predictions and to model complex systems in a more realistic way.
To understand the concept of impossible events, it is useful to consider some examples. For instance, if you toss a coin, the event of getting both heads and tails at the same time is impossible. Similarly, if you roll a standard six-sided die, the event of getting a seven is impossible. In both cases, these events are subsets of the sample space that have zero probability of occurring.
In practice, it is important to be able to identify impossible events and to understand their properties. For example, if you are working with a probabilistic model to estimate the likelihood of certain outcomes, it is important to be able to identify impossible events and to assign them a probability of zero. This allows you to make more accurate predictions and to model complex systems in a more realistic way.
Overall, the concept of “Probability and Statistics Different types of events (Impossible)” is an important aspect of probability theory that helps us to understand the properties of different events and to make more accurate predictions and models.
Case Study on Different types of events (Impossible)
Here is an example case study that demonstrates the use of “Probability and Statistics Different types of events (Impossible)”:
Case study: Rolling a standard six-sided die
Suppose you are rolling a standard six-sided die and you want to study the probability of different outcomes. In this case, the sample space consists of the numbers 1 through 6, and each outcome is equally likely.
One way to classify the different events is based on their likelihood or probability of occurrence. For example, we can classify the following events:
- Event A: rolling an even number (2, 4, or 6)
- Event B: rolling a number less than 2 (1)
- Event C: rolling a number greater than 6 (impossible event)
In this case, event A has a probability of 3/6 or 1/2, event B has a probability of 1/6, and event C has a probability of 0, since it is impossible.
We can also use these probabilities to make predictions about future outcomes. For example, if we roll the die many times, we would expect event A to occur about half of the time, event B to occur about one-sixth of the time, and event C to never occur.
Additionally, we can use these probabilities to calculate the probability of more complex events. For example, the probability of rolling a number less than 2 and an even number on two consecutive rolls is the product of the probabilities of the individual events: (1/6) * (1/2) = 1/12.
In this example, the concept of impossible events allows us to differentiate between events that can occur and events that cannot occur. This helps us to make more accurate predictions and to model the system in a more realistic way.
White paper on Different types of events (Impossible)
Here is a white paper on “Probability and Statistics Different types of events (Impossible)”:
Introduction:
Probability theory is a branch of mathematics that deals with the study of random events and the likelihood of their occurrence. Probability theory is used extensively in various fields such as finance, engineering, science, and business to model and analyze complex systems, estimate risks and make informed decisions. One of the fundamental concepts in probability theory is the classification of events based on their likelihood or probability of occurrence. Events can be classified into different types such as possible, certain, and impossible events.
This white paper focuses on the concept of “Probability and Statistics Different types of events (Impossible)” which refers to events that have zero probability of occurring.
Definition of Impossible Events:
An impossible event is a subset of the sample space that cannot occur. An impossible event has a probability of zero. The concept of impossible events is important in probability theory because it allows us to differentiate between events that can occur and events that cannot occur. This helps us to make more accurate predictions and to model complex systems in a more realistic way.
Examples of Impossible Events:
Consider the following examples of impossible events:
- Rolling a standard six-sided die and getting a number greater than six.
- Tossing a coin and getting both heads and tails at the same time.
- Drawing a card from a deck of cards and getting a card that is both red and black.
In each of these examples, the event is impossible because it is a subset of the sample space that has zero probability of occurring.
Properties of Impossible Events:
Some of the key properties of impossible events are:
- An impossible event has a probability of zero.
- An impossible event is a subset of the sample space that cannot occur.
- The probability of an impossible event is always less than or equal to the probability of any possible event.
Applications of Impossible Events:
The concept of impossible events has numerous applications in various fields such as:
- Finance: Probability theory is used in finance to model risk and to estimate the likelihood of different financial outcomes. Understanding the different types of events, including impossible events, is important in this context.
- Science: Probability theory is used in many branches of science, including physics, biology, and chemistry. The study of different types of events is important in analyzing experimental results and making predictions about future events.
- Engineering: Probability theory is used in engineering to model and analyze complex systems, and to estimate the probability of system failure. Understanding the different types of events, including impossible events, is important in this context.
- Business: Probability theory is used in business to analyze data and make informed decisions. Understanding the different types of events, including impossible events, is important in this context as well.
Conclusion:
In conclusion, the concept of “Probability and Statistics Different types of events (Impossible)” is a fundamental aspect of probability theory. It helps us to differentiate between events that can occur and events that cannot occur, and it allows us to make more accurate predictions and to model complex systems in a more realistic way. The concept of impossible events has numerous applications in various fields such as finance, science, engineering, and business, making it an important concept to understand and apply.