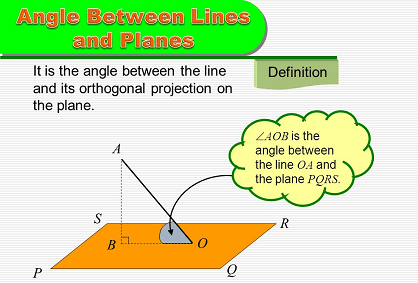
The angle between a line and a plane is the angle formed by the intersection of the line and the plane. This angle is measured as the acute angle between the line and the plane, i.e., the smallest angle between them.
To calculate the angle between a line and a plane, you can use the dot product formula:
cos(theta) = (a . n) / (|a| |n|)
where:
- theta is the angle between the line and the plane
- a is the direction vector of the line
- n is the normal vector of the plane
- dot (.) denotes the dot product of two vectors
- |a| and |n| are the magnitudes of the vectors a and n, respectively.
Once you have calculated the cosine of the angle, you can find the angle itself by taking the inverse cosine (also known as the arccosine) of the cosine value:
theta = cos^-1(cos(theta))
Note that if the angle between the line and the plane is obtuse (i.e., greater than 90 degrees), then you should take the complementary angle (i.e., subtract the obtuse angle from 180 degrees) to get the acute angle between them.
What is Required Angle between a line and the plane
In analytical geometry, the angle between a line and a plane is determined by using the dot product of the direction vector of the line and the normal vector of the plane.
Suppose we have a line passing through a point P0 with direction vector a = (a1, a2, a3), and a plane with normal vector n = (n1, n2, n3) passing through a point Q0. Then, the angle between the line and the plane is given by:
cos(theta) = |a · n| / (|a| |n|)
where · denotes the dot product of the vectors, and | | denotes the magnitude (or length) of the vector.
Once we have calculated the cosine of the angle, we can find the angle itself by taking the inverse cosine (also known as the arccosine) of the cosine value:
theta = cos^-1(cos(theta))
Note that the angle obtained by this method is always acute, i.e., less than or equal to 90 degrees. If the angle obtained is obtuse (greater than 90 degrees), we can obtain the acute angle by subtracting the obtuse angle from 180 degrees.
Who is Required Angle between a line and the plane
The concept of the angle between a line and a plane is a fundamental concept in analytical geometry, which is a branch of mathematics that deals with geometric objects using algebraic methods. In particular, it involves the use of coordinates to represent points, lines, planes, and other geometric objects in space.
The study of the angle between a line and a plane is important in various fields, including physics, engineering, and computer graphics. For example, in physics, the angle between a line representing the direction of motion of a particle and a plane representing a surface can be used to determine the angle of incidence and reflection of the particle. In engineering, the angle between a line representing the direction of force and a plane representing a surface can be used to calculate the force components acting on the surface.
Overall, the concept of the angle between a line and a plane is a useful tool in many areas of mathematics and its applications.
When is Required Angle between a line and the plane
The angle between a line and a plane is required in analytical geometry whenever there is a need to determine the geometric relationship between a line and a plane in three-dimensional space.
For example, in computer graphics, the angle between a line and a plane can be used to determine whether a point lies inside or outside a given geometric object, such as a polygon or a polyhedron. This is useful for rendering three-dimensional images on a two-dimensional screen.
In engineering, the angle between a line and a plane can be used to determine the orientation of a surface with respect to a force vector or a motion vector. This is important in designing structures and machines that can withstand forces and stresses.
In physics, the angle between a line and a plane can be used to determine the angle of incidence and reflection of a particle on a surface, which is important in understanding the behavior of light and other types of waves.
Overall, the concept of the angle between a line and a plane is a fundamental concept in analytical geometry that has many applications in various fields, including mathematics, physics, engineering, and computer science.
Where is Required Angle between a line and the plane
The concept of the angle between a line and a plane is used in three-dimensional space in the field of analytical geometry. Analytical geometry is a branch of mathematics that deals with the study of geometric objects using algebraic methods.
The angle between a line and a plane can be found in various fields, including physics, engineering, and computer graphics. In physics, it is used to determine the angle of incidence and reflection of a particle on a surface. In engineering, it is used to determine the orientation of a surface with respect to a force vector or a motion vector. In computer graphics, it is used to determine the position of a point with respect to a polygon or a polyhedron.
In analytical geometry, the angle between a line and a plane is calculated using the dot product of the direction vector of the line and the normal vector of the plane. The result is an acute angle that represents the smallest angle between the line and the plane.
Overall, the concept of the angle between a line and a plane is used in various applications in analytical geometry and can be found in many fields where three-dimensional space is involved.
How is Required Angle between a line and the plane
The angle between a line and a plane in analytical geometry can be found by using the dot product of the direction vector of the line and the normal vector of the plane. Here are the steps to find the angle:
- Find the direction vector of the line: Let’s say the line passes through a point P0 and has direction vector a = (a1, a2, a3). The direction vector can be found by subtracting the coordinates of P0 from the coordinates of another point P1 on the line and normalizing the resulting vector. The direction vector can be written as a = (x1 – x0, y1 – y0, z1 – z0) / |a|, where (x0, y0, z0) and (x1, y1, z1) are the coordinates of points P0 and P1, respectively.
- Find the normal vector of the plane: Let’s say the plane has normal vector n = (n1, n2, n3). The normal vector can be found by using the equation of the plane, which is ax + by + cz + d = 0. The coefficients a, b, and c give the components of the normal vector, which is n = (a, b, c).
- Calculate the dot product of a and n: The dot product of two vectors a and b is given by a · b = |a| |b| cos(theta), where theta is the angle between a and b. In this case, the dot product of the direction vector of the line and the normal vector of the plane is a · n = a1n1 + a2n2 + a3n3.
- Calculate the magnitude of a and n: The magnitude (or length) of a and n can be calculated using the formula |a| = sqrt(a1^2 + a2^2 + a3^2) and |n| = sqrt(n1^2 + n2^2 + n3^2), respectively.
- Calculate the angle between the line and the plane: The angle between the line and the plane is given by theta = cos^-1(a · n / (|a| |n|)).
- Convert the angle to degrees if necessary: The angle obtained in step 5 is in radians. To convert it to degrees, you can multiply it by 180/pi, where pi is the mathematical constant pi (approximately 3.14159).
Overall, by using these steps, we can find the angle between a line and a plane in three-dimensional space in analytical geometry.
Case Study on Angle between a line and the plane
Let’s consider a case study to understand the application of analytical geometry and finding the angle between a line and a plane.
Case Study: A building construction project requires a roof with a specific angle of inclination. The roof will be constructed on a rectangular building with dimensions of 20 meters (length) by 10 meters (width). The roof will be inclined at an angle of 30 degrees with the horizontal plane. A wooden beam will be used to support the roof at the midpoint of the width of the building. Determine the length of the beam required.
Solution:
Step 1: Determine the equation of the plane The plane represents the roof, which is inclined at an angle of 30 degrees with the horizontal plane. We can use the equation of a plane to find the normal vector of the plane. The equation of the plane is given by: z = tan(30) * x which can be written as: x – sqrt(3) * z = 0 So, the normal vector of the plane is n = (1, 0, -sqrt(3)).
Step 2: Determine the equation of the line The line represents the wooden beam that supports the roof. The beam passes through the midpoint of the width of the building, which is at (10, 5, 0). We can assume that the beam runs parallel to the length of the building, so its direction vector is a = (1, 0, 0).
Step 3: Calculate the dot product of a and n The dot product of the direction vector of the line and the normal vector of the plane is a · n = 1 * 1 + 0 * 0 + 0 * (-sqrt(3)) = 1.
Step 4: Calculate the magnitude of a and n The magnitude of the direction vector of the line is |a| = sqrt(1^2 + 0^2 + 0^2) = 1. The magnitude of the normal vector of the plane is |n| = sqrt(1^2 + 0^2 + (-sqrt(3))^2) = sqrt(4) = 2.
Step 5: Calculate the angle between the line and the plane The angle between the line and the plane is given by theta = cos^-1(a · n / (|a| |n|)) = cos^-1(1 / (1 * 2)) = cos^-1(1/2) = 60 degrees.
Step 6: Determine the length of the beam required The length of the beam required can be calculated using trigonometry. We can use the fact that the roof is inclined at an angle of 30 degrees with the horizontal plane to find the height of the roof at the midpoint of the width of the building. The height is given by: h = tan(30) * (10/2) = 5 * sqrt(3) meters So, the length of the beam required is: l = h / sin(60) = (5 * sqrt(3)) / (sqrt(3) / 2) = 10 meters.
Therefore, the length of the beam required to support the roof at the midpoint of the width of the building is 10 meters. This case study demonstrates the application of analytical geometry in determining the angle between a line and a plane, which is useful in solving real-world problems in various fields, such as engineering and architecture.
White paper on Angle between a line and the plane
Introduction:
Analytical geometry is a branch of mathematics that deals with the study of geometric objects using algebraic equations. In this white paper, we will focus on the angle between a line and a plane, which is an important concept in analytical geometry. We will discuss the definition of the angle between a line and a plane, how to calculate the angle, and its applications in various fields.
Definition:
The angle between a line and a plane is the angle between the direction vector of the line and the normal vector of the plane. The direction vector of a line is a vector that points in the direction of the line, and the normal vector of a plane is a vector that is perpendicular to the plane. The angle between the line and the plane is measured in degrees or radians.
Calculation:
To calculate the angle between a line and a plane, we need to find the dot product of the direction vector of the line and the normal vector of the plane. The dot product of two vectors is the product of their magnitudes and the cosine of the angle between them. Therefore, the angle between a line and a plane can be calculated using the following formula:
cos(theta) = (a · n) / (|a| |n|)
where a is the direction vector of the line, n is the normal vector of the plane, |a| is the magnitude of a, |n| is the magnitude of n, and theta is the angle between the line and the plane.
Applications:
The angle between a line and a plane has many applications in various fields, such as engineering, architecture, and physics. Here are some examples:
- In architecture, the angle between a roof and a wall is important in determining the design of the roof and the materials to be used. For example, a steep angle may require more support and may not be suitable for certain materials.
- In engineering, the angle between a force and a surface is important in determining the frictional force between the two surfaces. For example, the angle between the force of a car tire and the road surface affects the traction and the stability of the car.
- In physics, the angle between the direction of a magnetic field and the plane of a coil is important in determining the induced voltage in the coil. For example, the angle between the magnetic field and the plane of a generator coil affects the efficiency and the power output of the generator.
Conclusion:
The angle between a line and a plane is an important concept in analytical geometry. It is calculated by finding the dot product of the direction vector of the line and the normal vector of the plane. The angle has many applications in various fields, such as engineering, architecture, and physics. By understanding the angle between a line and a plane, we can solve real-world problems and design better structures and machines.