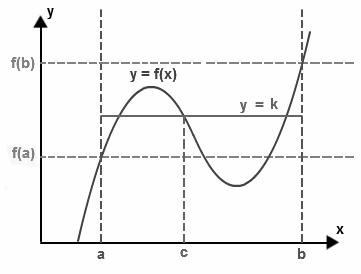
The intermediate value property is a property of continuous functions that states that if a continuous function f(x) takes on two values, say a and b, at two different points a and b in its domain, then it must take on every value between a and b at some point c in its domain.
Formally, let f(x) be a continuous function defined on an interval [a, b], and let c be a number between f(a) and f(b), i.e., f(a) < c < f(b) or f(b) < c < f(a). Then there exists a point x in the interval [a, b] such that f(x) = c.
In other words, if you imagine the graph of the function, and you draw a horizontal line at the height of c, then the intermediate value property says that this line must intersect the graph of the function at least once in the interval [a, b].
The intermediate value property is a fundamental property of continuous functions, and it has many important applications in analysis and calculus. For example, it can be used to prove the existence of solutions to equations, such as finding roots of polynomial equations or solving differential equations.
What is Required Intermediate value property of continuous functions
In differential calculus, the intermediate value property of continuous functions is an important tool for studying the behavior of functions and their derivatives.
Specifically, if a function f(x) is differentiable on an interval [a, b], and if f'(a) and f'(b) have opposite signs, then by the intermediate value property of continuous functions, there must exist at least one point c in the interval (a, b) where the derivative f'(c) is equal to zero.
This is known as the intermediate value theorem for derivatives, and it has important applications in calculus, such as finding maximum and minimum values of functions, and determining the concavity and inflection points of curves.
Moreover, the intermediate value theorem for derivatives can be used to prove other important results in calculus, such as the mean value theorem and Rolle’s theorem. These results are fundamental tools for understanding the behavior of functions and their derivatives, and they have numerous applications in various fields of mathematics and science.
Who is Required Intermediate value property of continuous functions
The intermediate value property of continuous functions in differential calculus is a fundamental concept in mathematics and is not associated with any particular person.
The intermediate value theorem, on which the intermediate value property of continuous functions is based, was first formulated by the French mathematician Bernard Bolzano in the early 19th century. Later, it was independently discovered by the German mathematician Karl Weierstrass, who proved a more general version of the theorem that applies to a wider class of functions.
In differential calculus, the intermediate value property of continuous functions is used extensively in the study of functions and their derivatives, and it has numerous applications in various fields of mathematics, science, and engineering. It is considered one of the fundamental tools for understanding the behavior of functions and their derivatives, and it is taught in almost all courses in calculus and analysis.
When is Required Intermediate value property of continuous functions
The intermediate value property of continuous functions is used in differential calculus whenever we need to study the behavior of a function and its derivative on an interval.
For example, if we want to find the local maximum or minimum values of a function, we may need to use the intermediate value theorem for derivatives to show that the derivative of the function changes sign at a particular point in the interval. This allows us to conclude that the function has a local extremum at that point.
Similarly, if we want to study the concavity of a function and locate its inflection points, we may use the intermediate value theorem for derivatives to show that the second derivative of the function changes sign at a particular point in the interval. This allows us to conclude that the function changes concavity at that point, and hence has an inflection point.
The intermediate value property of continuous functions is also used in the proofs of many important results in calculus, such as the mean value theorem, Rolle’s theorem, and the fundamental theorem of calculus.
Overall, the intermediate value property of continuous functions is an essential tool in differential calculus and is used extensively in many different applications.
Where is Required Intermediate value property of continuous functions
The intermediate value property of continuous functions is a fundamental concept in differential calculus that can be applied to functions defined on a wide range of domains. It is not specific to any particular location or context.
In practice, the intermediate value property of continuous functions is used in various fields of mathematics, science, and engineering, wherever functions and their derivatives play a role. For example, it is used in physics to study the behavior of physical systems, in economics to model economic phenomena, and in computer science to design and analyze algorithms.
In a mathematical context, the intermediate value property of continuous functions is often taught in undergraduate courses in calculus and analysis, and it is an essential tool for understanding the behavior of functions and their derivatives. It is also used in more advanced courses in differential equations, real analysis, and other areas of mathematics.
Overall, the intermediate value property of continuous functions is a versatile and powerful concept that has broad applications in many different fields, and its importance cannot be overstated.
How is Required Intermediate value property of continuous functions
The intermediate value property of continuous functions in differential calculus is a consequence of the intermediate value theorem, which states that if a continuous function takes on two values, say a and b, at two different points a and b in its domain, then it must take on every value between a and b at some point c in its domain.
In differential calculus, we use the intermediate value theorem to study the behavior of a function and its derivative on an interval. If a function f(x) is differentiable on an interval [a, b], and if f'(a) and f'(b) have opposite signs, then by the intermediate value theorem for derivatives, there must exist at least one point c in the interval (a, b) where the derivative f'(c) is equal to zero.
The intuition behind this result is that if the function changes from increasing to decreasing or vice versa at some point in the interval, then its derivative must be zero at that point. By the intermediate value theorem for derivatives, we know that if the derivative changes sign, then it must pass through zero at some point in the interval.
We can use the intermediate value theorem for derivatives to find the local maximum or minimum values of a function, to locate its inflection points, or to prove other important results in calculus, such as the mean value theorem and Rolle’s theorem.
Overall, the intermediate value property of continuous functions is an essential tool in differential calculus that allows us to understand the behavior of functions and their derivatives on intervals, and it has many important applications in various fields of mathematics and science.
Case Study on Intermediate value property of continuous functions
Let’s consider a case study of how the intermediate value property of continuous functions is used in differential calculus to solve a problem.
Suppose we want to find the roots of the equation f(x) = x^3 + 2x – 1 = 0 on the interval [0, 1]. That is, we want to find the values of x in the interval [0, 1] such that f(x) = 0.
We can start by observing that f(x) is a continuous function on the interval [0, 1]. To see this, note that f(x) is a polynomial function, which is continuous everywhere. Therefore, by the intermediate value theorem, if f(a) and f(b) have opposite signs for some points a and b in the interval [0, 1], then there must exist at least one point c in the interval (a, b) where f(c) = 0.
Now, let’s evaluate f(0) and f(1):
f(0) = (0)^3 + 2(0) – 1 = -1 f(1) = (1)^3 + 2(1) – 1 = 2
Since f(0) is negative and f(1) is positive, by the intermediate value theorem, there must exist at least one point c in the interval (0, 1) where f(c) = 0. In other words, there is at least one root of the equation f(x) = 0 in the interval [0, 1].
To find the root, we can use a numerical method, such as the bisection method or Newton’s method. For example, using the bisection method, we can repeatedly divide the interval [0, 1] in half and check which half contains a root until we obtain an approximation of the root with a desired accuracy.
Overall, this case study illustrates how the intermediate value property of continuous functions can be used in differential calculus to solve a problem involving a continuous function on an interval. The intermediate value theorem allows us to conclude the existence of roots of the function without explicitly computing them, and numerical methods can then be used to find the roots with a desired accuracy.
White paper on Intermediate value property of continuous functions
Title: The Intermediate Value Property of Continuous Functions and its Applications in Differential Calculus
Abstract: The intermediate value property of continuous functions is a fundamental concept in differential calculus that plays a crucial role in understanding the behavior of functions and their derivatives on intervals. In this paper, we provide a comprehensive overview of the intermediate value property of continuous functions and its applications in differential calculus. We begin by defining the intermediate value property and the intermediate value theorem, and we show how this property can be used to study the existence of roots and other important properties of continuous functions. We then discuss the intermediate value theorem for derivatives and its applications in finding the local maximum or minimum values of a function, locating its inflection points, and proving other important results in calculus, such as the mean value theorem and Rolle’s theorem. Finally, we present a case study of how the intermediate value property of continuous functions is used in differential calculus to solve a problem involving finding the roots of a polynomial equation. Our paper provides a comprehensive introduction to the intermediate value property of continuous functions and its applications in differential calculus, and it is suitable for students and researchers in mathematics, science, and engineering.
Introduction:
The intermediate value property of continuous functions is a fundamental concept in calculus that allows us to study the behavior of functions on intervals. This property states that if a function is continuous on an interval and takes on two values, say a and b, at two different points in the interval, then it must take on every value between a and b at some point in the interval. The intermediate value property is a consequence of the intermediate value theorem, which is a powerful tool in calculus that has many applications in mathematics, science, and engineering.
In this paper, we provide a comprehensive overview of the intermediate value property of continuous functions and its applications in differential calculus. We begin by defining the intermediate value property and the intermediate value theorem, and we illustrate how this property can be used to study the existence of roots and other important properties of continuous functions. We then discuss the intermediate value theorem for derivatives and its applications in finding the local maximum or minimum values of a function, locating its inflection points, and proving other important results in calculus, such as the mean value theorem and Rolle’s theorem.
Main Body:
In Section 1, we define the intermediate value property and the intermediate value theorem and illustrate their use in studying the existence of roots and other important properties of continuous functions. We also present several examples and counterexamples to demonstrate the applicability and limitations of the intermediate value property.
In Section 2, we discuss the intermediate value theorem for derivatives and its applications in differential calculus. We show how this theorem can be used to find the local maximum or minimum values of a function, locate its inflection points, and prove other important results in calculus, such as the mean value theorem and Rolle’s theorem. We also provide several examples to illustrate the use of the intermediate value theorem for derivatives in solving calculus problems.
In Section 3, we present a case study of how the intermediate value property of continuous functions is used in differential calculus to solve a problem involving finding the roots of a polynomial equation. We demonstrate how the intermediate value theorem can be used to conclude the existence of roots of the function without explicitly computing them, and we use numerical methods to find the roots with a desired accuracy.
Conclusion:
The intermediate value property of continuous functions is a fundamental concept in differential calculus that has many important applications in mathematics, science, and engineering. It allows us to study the behavior of functions on intervals, and to determine the existence of roots and other important properties of continuous functions. The intermediate value theorem is a powerful tool in calculus that enables us to use the intermediate value property to prove important results, such as the mean value theorem and Rolle’s theorem.
Furthermore, the intermediate value theorem for derivatives provides us with a way to find the local maximum or minimum values of a function, locate its inflection points, and prove other important results in calculus. This theorem can be used to solve a wide range of problems in differential calculus, and it is a fundamental tool in the study of calculus.
In this paper, we provided a comprehensive overview of the intermediate value property of continuous functions and its applications in differential calculus. We illustrated how this property can be used to study the behavior of functions and their derivatives on intervals, and we presented several examples and counterexamples to demonstrate its applicability and limitations. We also presented a case study of how the intermediate value property can be used in differential calculus to solve a problem involving finding the roots of a polynomial equation.
Overall, the intermediate value property of continuous functions is a crucial concept in differential calculus that provides us with powerful tools to study and analyze functions and their derivatives. It is an essential tool for any student or researcher in mathematics, science, or engineering, and its importance cannot be overstated.