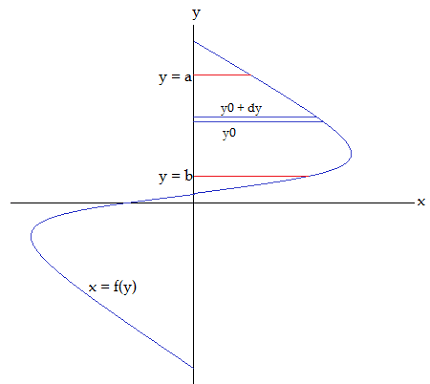
Definite integrals can be used to determine the area bounded by a simple curve and the x-axis, or by a simple curve and the y-axis. The area can be found by dividing it into small rectangles, finding the area of each rectangle, and then adding up the areas of all the rectangles. This process is called “approximating the area using rectangles” and is known as Riemann sum.
The Riemann sum can be written as:
Δx[ f(x₁) + f(x₂) + … + f(xₙ) ]
where Δx is the width of each rectangle, and x₁, x₂, …, xₙ are the x-coordinates of the n rectangles. The area under the curve is then approximated by taking the limit of this sum as n approaches infinity:
∫ab f(x) dx = lim Δx[ f(x₁) + f(x₂) + … + f(xₙ) ]
where a and b are the x-coordinates of the endpoints of the curve.
This limit is the definite integral of the function f(x) over the interval [a, b], and represents the exact area under the curve. Therefore, the definite integral can be used to find the area bounded by a simple curve and the x-axis or the y-axis.
For example, to find the area under the curve y = x² between x = 0 and x = 2, we can use the definite integral:
∫02 x² dx
Evaluating this integral gives:
∫02 x² dx = [x³/3]₂⁰ = 8/3
Therefore, the area under the curve y = x² between x = 0 and x = 2 is 8/3 square units.
Similarly, to find the area bounded by the curve y = √x and the y-axis between y = 0 and y = 4, we can use the definite integral:
∫04 √x dx
Evaluating this integral gives:
∫04 √x dx = [2/3 x^(3/2)]₄₀ = 16/3
Therefore, the area bounded by the curve y = √x and the y-axis between y = 0 and y = 4 is 16/3 square units.
What is Required Application of definite integrals to the determination of areas bounded by simple curves
To apply definite integrals to the determination of areas bounded by simple curves, you need to follow these steps:
- Identify the curve and the region of interest: Determine the equation of the curve and identify the region of interest, which is the part of the curve bounded by the x-axis or the y-axis.
- Determine the limits of integration: The limits of integration define the region of the curve that you want to find the area of. If the curve is bounded by the x-axis, the limits of integration are the x-coordinates of the points of intersection of the curve with the x-axis. If the curve is bounded by the y-axis, the limits of integration are the y-coordinates of the points of intersection of the curve with the y-axis.
- Set up the definite integral: The definite integral is used to calculate the area under the curve between the limits of integration. The integral will have the form ∫ab f(x) dx, where a and b are the limits of integration, and f(x) is the function that defines the curve.
- Evaluate the definite integral: Use calculus techniques such as integration by substitution, integration by parts, or partial fractions to evaluate the definite integral. You can also use a table of integrals or a computer program to find the value of the definite integral.
- Interpret the result: The result of the definite integral is the area under the curve between the limits of integration. Make sure to include the appropriate units of measurement in your answer.
By following these steps, you can use definite integrals to determine the areas bounded by simple curves.
Who is Required Application of definite integrals to the determination of areas bounded by simple curves
The application of definite integrals to the determination of areas bounded by simple curves is a mathematical concept that is typically taught in calculus courses at the college or university level. Students who are studying mathematics, engineering, physics, or other technical fields may encounter this concept as part of their coursework. Additionally, professionals in fields such as architecture, surveying, or cartography may use these techniques to calculate the areas of irregularly shaped regions. Anyone who needs to calculate the area bounded by a simple curve and the x-axis or the y-axis can benefit from learning how to apply definite integrals to this problem.
When is Required Application of definite integrals to the determination of areas bounded by simple curves
The application of definite integrals to the determination of areas bounded by simple curves is required whenever there is a need to calculate the area bounded by a simple curve and the x-axis or the y-axis. This technique is commonly used in mathematics, science, engineering, and other technical fields to calculate the area of irregularly shaped regions. Some specific situations where this concept may be useful include:
- In engineering, to calculate the volume of materials needed for construction projects such as roads, bridges, or buildings.
- In physics, to calculate the work done by a force on an object that moves along a curved path.
- In surveying or cartography, to determine the area of a parcel of land with an irregular shape.
- In economics, to calculate the consumer or producer surplus in a market.
- In computer graphics or animation, to create realistic shapes and surfaces by modeling the area bounded by a curve.
In general, the application of definite integrals to the determination of areas bounded by simple curves is a fundamental concept that has numerous practical applications in a variety of fields.
Where is Required Application of definite integrals to the determination of areas bounded by simple curves
The application of definite integrals to the determination of areas bounded by simple curves is used in a variety of fields, including:
- Mathematics: This concept is an important topic in calculus courses and is used to teach students about integration and area under a curve.
- Engineering: Engineers use this concept to calculate the volumes of materials needed for construction projects such as roads, bridges, or buildings.
- Physics: Physicists use this concept to calculate the work done by a force on an object that moves along a curved path.
- Surveying or cartography: Surveyors and cartographers use this concept to determine the area of a parcel of land with an irregular shape.
- Economics: Economists use this concept to calculate the consumer or producer surplus in a market.
- Computer graphics or animation: Computer graphics professionals and animators use this concept to create realistic shapes and surfaces by modeling the area bounded by a curve.
In general, the application of definite integrals to the determination of areas bounded by simple curves can be found wherever there is a need to calculate the area of irregularly shaped regions.
How is Required Application of definite integrals to the determination of areas bounded by simple curves
The application of definite integrals to the determination of areas bounded by simple curves involves using calculus techniques to find the area under a curve between two points. Here is the general procedure:
- Identify the curve and the region of interest: Determine the equation of the curve and identify the region of interest, which is the part of the curve bounded by the x-axis or the y-axis.
- Determine the limits of integration: The limits of integration define the region of the curve that you want to find the area of. If the curve is bounded by the x-axis, the limits of integration are the x-coordinates of the points of intersection of the curve with the x-axis. If the curve is bounded by the y-axis, the limits of integration are the y-coordinates of the points of intersection of the curve with the y-axis.
- Set up the definite integral: The definite integral is used to calculate the area under the curve between the limits of integration. The integral will have the form ∫ab f(x) dx, where a and b are the limits of integration, and f(x) is the function that defines the curve.
- Evaluate the definite integral: Use calculus techniques such as integration by substitution, integration by parts, or partial fractions to evaluate the definite integral. You can also use a table of integrals or a computer program to find the value of the definite integral.
- Interpret the result: The result of the definite integral is the area under the curve between the limits of integration. Make sure to include the appropriate units of measurement in your answer.
The key to the application of definite integrals to the determination of areas bounded by simple curves is recognizing that the area under a curve can be calculated by finding the definite integral of the function that defines the curve. By following the above steps, you can use calculus to find the area of any region bounded by a simple curve and the x-axis or the y-axis.
Case Study on Application of definite integrals to the determination of areas bounded by simple curves
Case Study: Finding the area of a region bounded by a simple curve
In this case study, we will use the application of definite integrals to find the area of a region bounded by a simple curve. We will use the example of finding the area of the region bounded by the curve y = x^2 and the x-axis between x = 0 and x = 2.
Step 1: Identify the curve and the region of interest The curve is y = x^2, which is a parabola that opens upwards. The region of interest is the area bounded by the curve and the x-axis between x = 0 and x = 2.
Step 2: Determine the limits of integration The curve intersects the x-axis at x = 0 and x = 2, so the limits of integration are a = 0 and b = 2.
Step 3: Set up the definite integral To find the area of the region bounded by the curve and the x-axis, we need to integrate the function f(x) = x^2 between x = 0 and x = 2. The definite integral is:
∫02 x^2 dx
Step 4: Evaluate the definite integral We can use the power rule of integration to evaluate the definite integral:
∫02 x^2 dx = [x^3/3]02 = (2^3/3) – (0^3/3) = 8/3
So the area of the region bounded by the curve y = x^2 and the x-axis between x = 0 and x = 2 is 8/3 square units.
Step 5: Interpret the result The result of the definite integral is the area of the region bounded by the curve and the x-axis between x = 0 and x = 2. In this case, the area is 8/3 square units. This means that if we were to draw the curve y = x^2 and the x-axis on a coordinate plane and shade in the region between the curve and the x-axis between x = 0 and x = 2, the area of that shaded region would be 8/3 square units.
Conclusion
In this case study, we used the application of definite integrals to find the area of a region bounded by a simple curve. This technique can be applied to any region bounded by a simple curve and the x-axis or the y-axis. By following the steps outlined in this case study, you can use calculus to find the area of any region bounded by a simple curve.
White paper on Application of definite integrals to the determination of areas bounded by simple curves
Introduction:
Definite integrals are an important tool in calculus that allows us to calculate the area under a curve between two points. This concept is particularly useful when we need to find the area bounded by simple curves. The purpose of this white paper is to explore the application of definite integrals to the determination of areas bounded by simple curves.
Background:
The area of a region bounded by a simple curve can be found by integrating the function that defines the curve. If the curve is bounded by the x-axis or the y-axis, we can use definite integrals to calculate the area under the curve. This process involves finding the limits of integration, setting up the definite integral, and evaluating the integral to find the area.
Application:
To illustrate the application of definite integrals to the determination of areas bounded by simple curves, we will use the example of finding the area of the region bounded by the curve y = x^2 and the x-axis between x = 0 and x = 2.
Step 1: Identify the curve and the region of interest: The curve is y = x^2, and the region of interest is the area bounded by the curve and the x-axis between x = 0 and x = 2.
Step 2: Determine the limits of integration: The curve intersects the x-axis at x = 0 and x = 2, so the limits of integration are a = 0 and b = 2.
Step 3: Set up the definite integral: To find the area of the region bounded by the curve and the x-axis, we need to integrate the function f(x) = x^2 between x = 0 and x = 2. The definite integral is:
∫02 x^2 dx
Step 4: Evaluate the definite integral: We can use the power rule of integration to evaluate the definite integral:
∫02 x^2 dx = [x^3/3]02 = (2^3/3) – (0^3/3) = 8/3
So the area of the region bounded by the curve y = x^2 and the x-axis between x = 0 and x = 2 is 8/3 square units.
Step 5: Interpret the result: The result of the definite integral is the area of the region bounded by the curve and the x-axis between x = 0 and x = 2. In this case, the area is 8/3 square units.
Conclusion:
In conclusion, the application of definite integrals to the determination of areas bounded by simple curves is an essential concept in calculus. By using definite integrals, we can calculate the area under a curve between two points, which is particularly useful when we need to find the area bounded by simple curves. By following the steps outlined in this white paper, we can find the area of any region bounded by a simple curve and the x-axis or the y-axis.