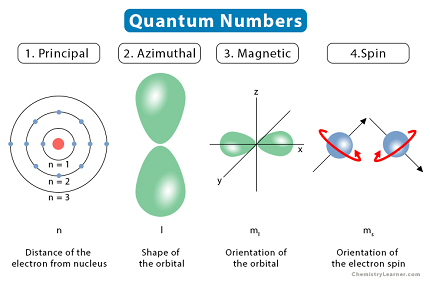
Quantum numbers are a set of numbers that describe the state of an electron in an atom or molecule. There are four quantum numbers:

1. Principal Quantum Number (n): This quantum number describes the energy level of the electron in an atom. It can have any positive integer value starting from 1, where n=1 represents the ground state or the lowest energy level.
2. Azimuthal Quantum Number (l): This quantum number describes the shape of the electron’s orbital. It can have any integer value between 0 and n-1. Each value of l corresponds to a different subshell. For example, if n=2, l can be either 0 or 1, which corresponds to the s and p subshells, respectively.
3. Magnetic Quantum Number (m): This quantum number describes the orientation of the electron’s orbital in space. It can have any integer value between -l and +l, including 0. Each value of m corresponds to a different orbital within a subshell. For example, if l=1 (p subshell), m can be -1, 0, or 1, which correspond to the three p orbitals (px, py, pz).
4. Spin Quantum Number (s): This quantum number describes the intrinsic angular momentum or “spin” of the electron. It can have only two values, +1/2 or -1/2, representing the two possible spin states of the electron.

Together, these four quantum numbers provide a unique set of parameters that describe the state of an electron in an atom or molecule.

What is Required Quantum numbers

In quantum mechanics, the state of an electron in an atom can be described by four quantum numbers:

1. Principal Quantum Number (n): It describes the energy level or shell that the electron occupies in an atom. The values of n are positive integers (1, 2, 3, …) with larger values of n indicating higher energy levels.
2. Azimuthal Quantum Number (l): It describes the shape of the electron’s orbital or subshell. The values of l depend on the value of n and range from 0 to (n-1). For example, if n=2, then l can be either 0 or 1.
3. Magnetic Quantum Number (m): It describes the orientation of the electron’s orbital in space. The values of m depend on the value of l and range from -l to +l. For example, if l=1, then m can be -1, 0, or +1.
4. Spin Quantum Number (s): It describes the intrinsic angular momentum or spin of the electron. The values of s are either +1/2 or -1/2, indicating the two possible spin states of an electron.

Together, these four quantum numbers completely describe the state of an electron in an atom, including its energy, shape, orientation, and spin.

Who is Required Quantum numbers

“Required Quantum numbers” is not a person, but rather a term used in quantum mechanics to describe the four quantum numbers (principal quantum number, azimuthal quantum number, magnetic quantum number, and spin quantum number) that are required to describe the state of an electron in an atom. These quantum numbers were first introduced by the physicist Arnold Sommerfeld in 1916, building on the earlier work of Niels Bohr on the structure of atoms. The Required Quantum numbers are an essential part of the quantum mechanical description of atoms and are used to understand the electronic configuration of atoms and their chemical properties.

When is Required Quantum numbers

The term “Required Quantum numbers” does not refer to a specific time or event. Rather, the concept of quantum numbers has been a fundamental part of quantum mechanics since the early 20th century when physicists like Niels Bohr, Arnold Sommerfeld, and others were developing the theory to describe the behavior of atoms and subatomic particles. The concept of quantum numbers is still used today in modern quantum mechanics to describe the electronic structure of atoms, molecules, and other systems. Quantum numbers are essential for understanding how electrons are distributed in atoms and how they interact with each other and with external fields. Therefore, the concept of quantum numbers is always relevant whenever we study the behavior of matter at the atomic and subatomic level.

Where is Required Quantum numbers

The term “Required Quantum numbers” does not refer to a physical location. Rather, it is a concept used in the field of quantum mechanics to describe the electronic structure of atoms, molecules, and other quantum systems. The Required Quantum numbers are mathematical parameters that describe the energy, angular momentum, orientation, and spin of an electron in an atom. They are used to calculate the probabilities of various electron states and transitions, and to predict the spectral lines and chemical properties of atoms. Therefore, the concept of quantum numbers is not located in a specific physical place, but rather it is a fundamental part of the mathematical framework that describes the behavior of matter at the atomic and subatomic level.

How is Required Quantum numbers

The Required Quantum numbers are a set of mathematical parameters that are used to describe the energy, angular momentum, orientation, and spin of an electron in an atom. Each electron in an atom is characterized by a unique set of four quantum numbers: the principal quantum number (n), the azimuthal quantum number (l), the magnetic quantum number (m), and the spin quantum number (s).

The principal quantum number (n) describes the energy level or shell that the electron occupies in the atom. The value of n can be any positive integer (1, 2, 3, …), and it determines the size of the electron’s orbital.

The azimuthal quantum number (l) describes the shape of the electron’s orbital or subshell. The values of l depend on the value of n and range from 0 to (n-1). For example, if n=2, then l can be either 0 or 1, which correspond to the s and p subshells, respectively.

The magnetic quantum number (m) describes the orientation of the electron’s orbital in space relative to a magnetic field. The values of m depend on the value of l and range from -l to +l. For example, if l=1, then m can be -1, 0, or +1, which correspond to the three possible orientations of the p subshell.

The spin quantum number (s) describes the intrinsic angular momentum or spin of the electron. The values of s are either +1/2 or -1/2, indicating the two possible spin states of an electron.

Together, these four quantum numbers completely describe the state of an electron in an atom, including its energy, shape, orientation, and spin. The Required Quantum numbers are used in mathematical equations to calculate the probabilities of various electron states and transitions, and to predict the spectral lines and chemical properties of atoms.

Case Study on Quantum numbers

Here’s a hypothetical case study on how quantum numbers can be used to describe the electronic structure of an atom:

Let’s consider the element carbon, which has an atomic number of 6. This means that a neutral carbon atom has six electrons distributed in its orbitals.

To describe the electronic structure of carbon using quantum numbers, we first assign the principal quantum number (n) for each electron. The first two electrons will occupy the lowest energy level, which corresponds to n=1. The remaining four electrons will occupy the second energy level, which corresponds to n=2.

Next, we assign the azimuthal quantum number (l) for each electron. For the n=1 electrons, l=0 because they occupy the s subshell, which has a spherical shape. For the n=2 electrons, two electrons will occupy the s subshell (l=0) and the remaining two electrons will occupy the p subshell (l=1).

Then, we assign the magnetic quantum number (m) for each electron. For the n=1 electrons, m=0 because there is only one possible orientation for the s subshell. For the n=2 electrons in the s subshell, m=0 as well because there is only one possible orientation for the spherical s subshell. For the n=2 electrons in the p subshell, m can be -1, 0, or +1 because there are three possible orientations for the dumbbell-shaped p subshell.

Finally, we assign the spin quantum number (s) for each electron, which can be either +1/2 or -1/2. The four electrons in the second energy level can have two possible spin states, which we can designate as up and down.

Using this information, we can write the electronic configuration of carbon as:

1s2 2s2 2p2

This means that the first two electrons are in the 1s subshell, the next two electrons are in the 2s subshell, and the last two electrons are in the 2p subshell. The quantum numbers provide a precise description of how these electrons are distributed in the atom’s orbitals, which determines its chemical properties and behavior.

White paper on Quantum numbers

Here’s a brief white paper on quantum numbers:

Quantum numbers are a set of mathematical parameters that describe the energy, angular momentum, orientation, and spin of an electron in an atom. They were first introduced in the early 20th century as part of the development of quantum mechanics, which aimed to describe the behavior of atoms and subatomic particles.

There are four quantum numbers that are used to describe the electronic structure of atoms: the principal quantum number (n), the azimuthal quantum number (l), the magnetic quantum number (m), and the spin quantum number (s).

The principal quantum number (n) describes the energy level or shell that the electron occupies in the atom. The value of n can be any positive integer, and it determines the size of the electron’s orbital.

The azimuthal quantum number (l) describes the shape of the electron’s orbital or subshell. The values of l depend on the value of n and range from 0 to (n-1).

The magnetic quantum number (m) describes the orientation of the electron’s orbital in space relative to a magnetic field. The values of m depend on the value of l and range from -l to +l.

The spin quantum number (s) describes the intrinsic angular momentum or spin of the electron. The values of s are either +1/2 or -1/2, indicating the two possible spin states of an electron.

Together, these four quantum numbers completely describe the state of an electron in an atom, including its energy, shape, orientation, and spin. The quantum numbers are used in mathematical equations to calculate the probabilities of various electron states and transitions, and to predict the spectral lines and chemical properties of atoms.

Quantum numbers have a wide range of applications in physics and chemistry, including the study of atomic and molecular structure, the behavior of subatomic particles, and the properties of materials. They are an essential tool for understanding the behavior of matter at the atomic and subatomic level.

In summary, quantum numbers are a set of mathematical parameters that provide a precise description of the electronic structure of atoms. They are a fundamental part of the mathematical framework that describes the behavior of matter at the atomic and subatomic level, and they have important applications in a wide range of fields.