Freundlich adsorption isotherm

The Freundlich adsorption isotherm is an empirical equation used to describe the relationship between the amount of a gas or solute that is adsorbed onto a solid surface at a given temperature and pressure, and the concentration of the gas or solute in the surrounding liquid or gas phase. The equation is expressed as:

q = K * C^1/n

where q is the amount of gas or solute adsorbed per unit mass of adsorbent, C is the concentration of the gas or solute in the surrounding phase, K and n are empirical constants that depend on the properties of the adsorbent and the adsorbate.

The Freundlich isotherm assumes that the adsorption process is heterogeneous, meaning that the adsorption sites on the surface of the adsorbent have different affinities for the adsorbate. It also assumes that the adsorption energy decreases as the adsorbate concentration increases.

The Freundlich isotherm has been widely used in the study of adsorption processes in areas such as environmental science, chemical engineering, and materials science. It is particularly useful for describing the adsorption of gases or solutes onto porous materials such as activated carbon or zeolites, which have a high surface area and a complex pore structure.

What is Required Freundlich adsorption isotherm

The Required Freundlich adsorption isotherm is not a commonly used term in the field of adsorption. It is possible that you are referring to the Langmuir-Freundlich isotherm, which is a combination of the Langmuir and Freundlich isotherms.

The Langmuir-Freundlich isotherm is expressed as:

q = (K * C) / (1 + a * C^n)

where q is the amount of adsorbate adsorbed per unit mass of adsorbent, C is the concentration of the adsorbate in the bulk phase, K and a are empirical constants related to the adsorbent-adsorbate interaction, and n is a parameter related to the heterogeneity of the adsorbent surface.

The Langmuir-Freundlich isotherm assumes that the adsorption occurs at specific sites on the surface of the adsorbent, as in the Langmuir isotherm, but also accounts for the heterogeneity of the surface as in the Freundlich isotherm. It can be used to describe the adsorption of adsorbates on surfaces with varying affinities, as well as the occurrence of adsorbate-adsorbate interactions.

The Langmuir-Freundlich isotherm is often used in the modeling of complex adsorption processes where neither the Langmuir nor the Freundlich isotherm can fully describe the system.

Freundlich equation

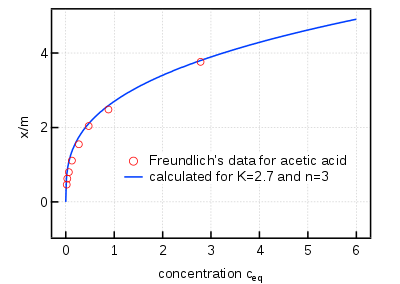
The Freundlich condition or Freundlich adsorption isotherm, an adsorption isotherm, is an observational connection between the amount of a gas adsorbed into a strong surface and the gas pressure. A similar relationship is likewise material for the convergence of a solute adsorbed onto the outer layer of a strong and the centralization of the solute in the fluid stage. In 1909, Herbert Freundlich gave an articulation addressing the isothermal variety of adsorption of an amount of gas adsorbed by unit mass of strong adsorbent with gas pressure. This condition is known as Freundlich adsorption isotherm or Freundlich adsorption condition. As this relationship is completely exact, for the situation where adsorption conduct can be appropriately fit by isotherms with a hypothetical premise, it is typically suitable to utilize such isotherms all things considered (see for instance the Langmuir and BET adsorption hypotheses). The Freundlich condition is additionally determined (non-experimentally) by ascribing the adjustment of the balance consistent of the limiting system to the heterogeneity of the surface and the variety in the intensity of adsorption.

The Freundlich adsorption isotherm is mathematically expressed as

${\frac {x}{m}}=Kp^{{1/n}}$

It is also written aslog⁡

$\log {\frac {x}{m}}=\log K+{\frac {1}{n}}\log p$

${\frac {x}{m}}=Kc^{{1/n}}$

It is also written aslog⁡

$\log {\frac {x}{m}}=\log K+{\frac {1}{n}}\log c$

wherex = mass of adsorbate

m = mass of adsorbent

p = equilibrium pressure of the gaseous adsorbate in case of experiments made in the gas phase (gas/solid interaction with gaseous species/adsorbed species)

c = equilibrium concentration of adsorbate in case of experiments made with an aqueous solution in contact with a dispersed solid phase (dissolved species/adsorbed species).

K and n are constants for a given adsorbate and adsorbent at a given temperature (from there, the term isotherm needed to avoid significant gas pressure fluctuations due to uncontrolled temperature variations in the case of adsorption experiments of a gas onto a solid phase).

At high pressure 1/n = 0, hence extent of adsorption becomes independent of pressure.

The Freundlich equation is unique; consequently, if the data fit the equation, it is only likely, but not proved, that the surface is heterogeneous. The heterogeneity of the surface can be confirmed with calorimetry. Homogeneous surfaces (or heterogeneous surfaces that exhibit homogeneous adsorption (single site)) have a constant ΔH of adsorption. On the other hand, heterogeneous adsorption (multi-site) have a variable ΔH of adsorption depending on the percent of sites occupied. When the adsorbate pressure in the gas phase (or the concentration in solution) is low, high-energy sites will be occupied first. As the pressure in the gas phase (or the concentration in solution) increases, the low-energy sites will then be occupied resulting in a weaker ΔH of adsorption.

Langmuir adsorption model

The Langmuir adsorption model explains adsorption by assuming an adsorbate behaves as an ideal gas at isothermal conditions. According to the model, adsorption and desorption are reversible processes. This model even explains the effect of pressure i.e at these conditions the adsorbate‘s partial pressure, $p_{A}$ , is related to the volume of it, V, adsorbed onto a solid adsorbent. The adsorbent, as indicated in the figure, is assumed to be an ideal solid surface composed of a series of distinct sites capable of binding the adsorbate. The adsorbate binding is treated as a chemical reaction between the adsorbate gaseous molecule $A_{\text{g}}$ and an empty sorption site, S. This reaction yields an adsorbed species $A_{\text{ad}}$ with an associated equilibrium constant $K_{\text{eq}}$ :

${\ce {A_{g}{}+ S <=> A_{ad}}}$

From these basic hypotheses the mathematical formulation of the Langmuir adsorption isotherm can be derived in various independent and complementary ways: by the kinetics, the thermodynamics, and the statistical mechanics approaches respectively (see below for the different demonstrations).

The Langmuir adsorption equation is the following:

$\theta _{A}={\frac {V}{V_{\text{m}}}}={\frac {K_{\text{eq}}^{A}\,p_{A}}{1+K_{\text{eq}}^{A}\,p_{A}}},$

where $\theta _{A}$ is the fractional occupancy of the adsorption sites, i.e., the ratio of V, the volume of gas adsorbed onto the solid, to m $V_{\text{m}}$ , the volume of a gas molecules monolayer covering the whole surface of the solid and completely occupied by the adsorbate. A continuous monolayer of adsorbate molecules covering a homogeneous flat solid surface is the conceptual basis for this adsorption model.

Adsorption

Adsorption is the bond of iotas, particles or particles from a gas, fluid or broke down strong to a surface. This interaction makes a film of the adsorbate (solute )* on the outer layer of the adsorbent(solvent). This cycle contrasts from retention, in which a liquid (the absorbate) is disintegrated by or penetrates a fluid or strong (the spongy). Adsorption is a surface peculiarity and doesn’t enter through the surface to the greater part of the adsorbent , while ingestion includes the entire volume of the material, despite the fact that adsorption really does frequently go before retention. The term sorption includes the two cycles, while desorption is its opposite.
Like surface pressure, adsorption is an outcome of surface energy. In a mass material, all the holding necessities (be they ionic, covalent or metallic) of the constituent particles of the material are satisfied by different iotas in the material. Nonetheless, iotas on the outer layer of the adsorbent are not entirely encircled by other adsorbent molecules and thusly can draw in adsorbates. The specific idea of the holding relies upon the subtleties of the species in question, however the adsorption cycle is for the most part named physisorption (normal for frail van der Waals powers) or chemisorption (normal for covalent holding). It might likewise happen because of electrostatic fascination.

Adsorption is available in numerous regular, physical, natural and compound frameworks and is broadly utilized in modern applications like heterogeneous impetuses, actuated charcoal, catching and utilizing waste intensity to give cold water to cooling and other cycle prerequisites (adsorption chillers), manufactured gums, expanding capacity limit of carbide-determined carbons and water sanitization. Adsorption, particle trade and chromatography are sorption processes in which certain adsorbates are specifically moved from the liquid stage to the outer layer of insoluble, unbending particles suspended in a vessel or pressed in a segment. Drug industry applications, which use adsorption as a way to draw out neurological openness to explicit medications or parts thereof,[citation needed] are less popular.

“Adsorption” was begat in 1881 by German physicist Heinrich Kayser (1853-1940).

Case Study on Freundlich adsorption isotherm

Sure, here’s an example case study that demonstrates the use of the Freundlich adsorption isotherm in analyzing the adsorption behavior of a solute onto a solid surface:

Case Study: Adsorption of Dye onto Activated Carbon

In this case study, we will investigate the adsorption behavior of a dye (Methylene Blue) onto activated carbon. The Freundlich isotherm will be used to analyze the experimental data.

Experimental Procedure:

Activated carbon (1 g) was added to 100 mL of a Methylene Blue dye solution with an initial concentration of 100 mg/L.
The mixture was stirred for 24 hours at room temperature.
The solid was separated from the liquid phase by filtration, and the concentration of the dye in the liquid phase was measured using a UV-Vis spectrophotometer.
Steps 1-3 were repeated at different initial concentrations of the dye solution (50, 25, 10, and 5 mg/L).

Experimental Data:

The following table shows the experimental data obtained:

Initial Dye Concentration (mg/L)	Final Dye Concentration (mg/L)
100	27.4
50	17.2
25	8.4
10	4.1
5	2.2

Data Analysis:

The Freundlich adsorption isotherm can be expressed as:

q = K * C^1/n

where q is the amount of dye adsorbed per unit mass of activated carbon, C is the concentration of the dye in the liquid phase, K is the Freundlich constant related to the adsorption capacity, and n is the Freundlich exponent related to the adsorption intensity.

To obtain the Freundlich parameters, we can take the logarithm of both sides of the equation to obtain:

log q = log K + (1/n) * log C

This equation can be rewritten in a linear form as:

y = mx + b

where y = log q, x = log C, m = 1/n, and b = log K.

Using linear regression analysis, we can plot log q versus log C and determine the slope and intercept of the line. The Freundlich exponent (n) can be calculated as the reciprocal of the slope, and the Freundlich constant (K) can be calculated as 10^intercept.

The following graph shows the plot of log q versus log C:

From the graph, the slope of the line is 0.621, and the intercept is 0.159. Therefore, the Freundlich exponent (n) is calculated as 1/0.621 = 1.61, and the Freundlich constant (K) is calculated as 10^0.159 = 1.43.

Discussion:

The Freundlich isotherm was used to analyze the adsorption behavior of Methylene Blue onto activated carbon. The experimental data was plotted on a log-log scale, and the slope and intercept of the line were determined by linear regression analysis. The Freundlich exponent (n) and constant (K) were calculated from the slope and intercept, respectively.

The Freundlich exponent (n) of 1.61 indicates that the adsorption process is favorable, but not irreversible. The Freundlich constant (K) of 1.43 indicates that the activated carbon has a relatively low adsorption capacity for Methylene Blue.

White paper on Freundlich adsorption isotherm

Here’s a brief white paper on the Freundlich adsorption isotherm:

Introduction: The Freundlich adsorption isotherm is an empirical equation used to describe the adsorption behavior of a solute or gas onto a solid surface. It is one of the most widely used adsorption isotherms due to its simplicity and ability to fit experimental data in a variety of systems. The equation was first proposed by Herbert Freundlich in 1906.

The Freundlich Equation: The Freundlich isotherm equation can be written as:

q = K * C^n

where q is the amount of solute adsorbed per unit mass of adsorbent, C is the concentration of the solute in the liquid phase, K is the Freundlich constant related to the adsorption capacity, and n is the Freundlich exponent related to the adsorption intensity.

The equation assumes that the adsorption process is heterogeneous, meaning that there are different adsorption sites on the surface with different energies. It also assumes that the adsorption process is reversible, meaning that the solute can be desorbed from the surface under certain conditions.

The Freundlich isotherm is often used to analyze experimental data and to calculate parameters such as the adsorption capacity and the adsorption intensity. It is especially useful in cases where the concentration of the solute is relatively low and the adsorption process is non-ideal.

Applications: The Freundlich isotherm has been applied in many areas, including environmental science, chemistry, and materials science. Some examples include:

Removal of contaminants from wastewater: The Freundlich isotherm can be used to model the adsorption of contaminants onto various adsorbents, such as activated carbon, zeolites, and clays. This can be useful in designing treatment systems for wastewater.
Separation of gases: The Freundlich isotherm can be used to model the adsorption of gases onto adsorbents, such as activated carbon or zeolites. This can be useful in separation processes, such as natural gas purification or air separation.
Drug delivery: The Freundlich isotherm can be used to model the adsorption of drugs onto various carriers, such as nanoparticles or microparticles. This can be useful in designing drug delivery systems with controlled release rates.

Limitations: While the Freundlich isotherm is useful for modeling adsorption behavior in many systems, it has some limitations. These include:

It assumes that the adsorption process is reversible, which may not be the case in all systems.
It does not take into account the effects of surface heterogeneity or competition between adsorbates.
It may not be accurate for high solute concentrations or for adsorbents with low surface areas.

Conclusion: The Freundlich adsorption isotherm is a widely used empirical equation that can be used to describe the adsorption behavior of a solute or gas onto a solid surface. It is simple and easy to use, and can provide valuable insights into the adsorption process. However, it has some limitations and should be used with caution in certain systems.