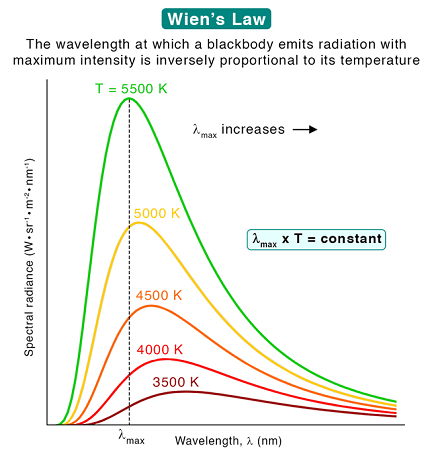
Wien’s displacement law, named after Wilhelm Wien, states that the peak wavelength of radiation emitted by a black body is inversely proportional to its temperature.
Mathematically, Wien’s displacement law can be expressed as λ_max = b/T, where λ_max is the peak wavelength of the radiation emitted by the black body, T is its temperature in kelvins, and b is a constant known as Wien’s displacement constant. The value of Wien’s displacement constant is approximately equal to 2.898 x 10^-3 mK, where mK denotes meters times kelvins.
Wien’s displacement law is one of the basic laws of radiation physics and has important applications in fields such as astrophysics and thermal engineering. It provides a basis for understanding the spectral distribution of energy emitted by objects at different temperatures, and is a fundamental principle in the study of thermal radiation.
What is Required Wien’s displacement law
Wien’s displacement law requires knowledge of the temperature and the peak wavelength of the radiation emitted by a black body. The temperature can be measured in kelvins using a thermometer, while the peak wavelength can be determined from the spectral distribution of the radiation using a spectrometer or other appropriate instruments.
It is important to note that Wien’s displacement law applies only to black bodies, which are hypothetical objects that absorb all radiation that falls on them and emit radiation in a continuous spectrum. While real objects do not behave exactly like black bodies, many objects can be approximated as such, and Wien’s displacement law can be used to calculate the peak wavelength of their radiation.
In addition, Wien’s displacement law assumes that the radiation emitted by the black body is in thermal equilibrium with its surroundings, meaning that the radiation energy emitted by the black body is equal to the energy absorbed from its surroundings.
When is Required Wien’s displacement law
Wien’s displacement law is required whenever there is a need to understand the spectral distribution of energy emitted by an object at a certain temperature. It is particularly useful in the field of thermal radiation, where it is used to calculate the peak wavelength of radiation emitted by a black body at a given temperature.
Wien’s displacement law also finds application in astrophysics, where it is used to determine the temperature of stars based on the wavelength of their emitted radiation. Additionally, it is used in thermal engineering to design and optimize the performance of devices that emit or absorb thermal radiation, such as heat exchangers and solar cells.
Overall, Wien’s displacement law is a fundamental principle in the study of thermal radiation, and it has important applications in a wide range of fields where the understanding of thermal processes and radiation is necessary.
Where is Required Wien’s displacement law
Wien’s displacement law is required in a variety of fields and applications where the spectral distribution of energy emitted by objects at different temperatures is important. Here are some examples:
- Astrophysics: Wien’s displacement law is used to determine the temperature of stars based on the wavelength of their emitted radiation. This helps astronomers understand the properties of stars and their evolution.
- Thermal engineering: Wien’s displacement law is used in the design and optimization of devices that emit or absorb thermal radiation, such as heat exchangers and solar cells. It also plays a role in the design of materials with specific thermal properties.
- Materials science: Wien’s displacement law is used in the study of materials that emit or absorb thermal radiation, such as ceramics and polymers. It helps researchers understand the thermal properties of these materials and how they can be used in various applications.
- Climate science: Wien’s displacement law is used to model the radiation emitted by the Earth and its atmosphere, which is important for understanding climate change and predicting future climate scenarios.
Overall, Wien’s displacement law is a fundamental principle in the study of thermal radiation and has broad applications in many fields.
How is Required Wien’s displacement law
Wien’s displacement law can be used to calculate the peak wavelength of radiation emitted by a black body at a given temperature. The law states that the peak wavelength is inversely proportional to the temperature, and this relationship can be expressed mathematically as:
λmax = b/T
where λmax is the peak wavelength of the radiation emitted by the black body, T is its temperature in kelvins, and b is a constant known as Wien’s displacement constant, which has a value of approximately 2.898 x 10^-3 mK.
To use Wien’s displacement law, one needs to measure the temperature of the black body and determine the peak wavelength of its emitted radiation. This can be done using a thermometer to measure the temperature and a spectrometer or other appropriate instruments to determine the spectral distribution of the radiation.
Once the temperature and peak wavelength have been determined, Wien’s displacement law can be used to calculate the peak wavelength of the radiation emitted by the black body at that temperature.
It is important to note that Wien’s displacement law applies only to black bodies, which are hypothetical objects that absorb all radiation that falls on them and emit radiation in a continuous spectrum. While real objects do not behave exactly like black bodies, many objects can be approximated as such, and Wien’s displacement law can be used to calculate the peak wavelength of their radiation.
Case Study on Wien’s displacement law
One example of the use of Wien’s displacement law is in the field of astrophysics, where it is used to determine the temperature of stars based on the wavelength of their emitted radiation.
Astronomers use telescopes to observe the light emitted by stars, and they can use the spectral distribution of this light to determine the temperature of the star. According to Wien’s displacement law, the peak wavelength of the radiation emitted by a star is inversely proportional to its temperature. Therefore, by measuring the peak wavelength of the radiation emitted by a star, astronomers can use Wien’s displacement law to calculate the temperature of the star.
For example, if a star emits most of its radiation at a wavelength of 500 nanometers (nm), we can use Wien’s displacement law to determine its temperature. The peak wavelength of the radiation emitted by the star (λmax) is related to its temperature (T) by the equation:
λmax = b/T
where b is Wien’s displacement constant. Solving for T, we get:
T = b/λmax
Using the value of Wien’s displacement constant (b = 2.898 x 10^-3 mK) and the wavelength of 500 nm, we can calculate the temperature of the star:
T = (2.898 x 10^-3 mK) / (500 nm) = 5800 K
This means that the star has a temperature of 5800 kelvins. Astronomers can use this information to better understand the properties of the star, such as its age, size, and composition.
In summary, Wien’s displacement law is a powerful tool that allows astronomers to determine the temperature of stars based on the wavelength of their emitted radiation. This has important implications for our understanding of the properties and behavior of stars, as well as the evolution of the universe as a whole.
White paper on Wien’s displacement law
Introduction:
Wien’s displacement law is a fundamental principle in the study of thermal radiation that describes the spectral distribution of energy emitted by objects at different temperatures. It is an important law that has wide-ranging applications in various fields, including astrophysics, thermal engineering, materials science, and climate science.
This white paper aims to provide an overview of Wien’s displacement law, including its history, mathematical expression, and practical applications. It will also discuss the limitations and assumptions of the law, as well as its significance in our understanding of thermal radiation and its role in different fields.
History:
Wien’s displacement law is named after German physicist Wilhelm Wien, who first formulated the law in 1893. Wien was studying the properties of blackbody radiation, which is the thermal radiation emitted by an object that absorbs all radiation that falls on it. He observed that the spectral distribution of energy emitted by a black body shifted towards shorter wavelengths as the temperature increased, and he proposed a mathematical expression to describe this relationship.
Mathematical expression:
Wien’s displacement law states that the wavelength of the maximum intensity of thermal radiation emitted by a black body is inversely proportional to the temperature of the object. This can be expressed mathematically as:
λmax = b/T
where λmax is the wavelength of the maximum intensity of radiation emitted by the black body, T is the temperature of the object in kelvins, and b is Wien’s displacement constant, which has a value of approximately 2.898 x 10^-3 mK.
The law implies that hotter objects emit radiation at shorter wavelengths than cooler objects. For example, the peak wavelength of radiation emitted by the sun, which has a temperature of approximately 5800 K, is in the visible range of the electromagnetic spectrum (around 500 nm). On the other hand, a cooler object such as the Earth, with a temperature of approximately 288 K, emits radiation at longer wavelengths, primarily in the infrared range (around 10 micrometers).
Applications:
Wien’s displacement law has many practical applications in different fields. One of the most important is in astrophysics, where it is used to determine the temperature of stars based on the wavelength of their emitted radiation. By measuring the peak wavelength of the radiation emitted by a star, astronomers can use Wien’s displacement law to calculate its temperature, which is crucial for understanding its properties and behavior.
Wien’s displacement law is also important in thermal engineering, where it is used in the design and optimization of devices that emit or absorb thermal radiation, such as heat exchangers and solar cells. It is also used in materials science to study the thermal properties of materials that emit or absorb radiation, such as ceramics and polymers.
Climate science is another field where Wien’s displacement law finds application. It is used to model the radiation emitted by the Earth and its atmosphere, which is important for understanding climate change and predicting future climate scenarios.
Limitations and assumptions:
It is important to note that Wien’s displacement law applies only to ideal black bodies, which absorb all radiation that falls on them and emit radiation in a continuous spectrum. In reality, no object behaves exactly like a black body, and deviations from this ideal behavior must be taken into account in many practical applications.
Additionally, Wien’s displacement law assumes that the radiation emitted by the object is in thermal equilibrium with its surroundings, meaning that the rate of energy absorbed by the object is equal to the rate of energy emitted. This is not always the case in real-world scenarios, where factors such as non-uniform temperature distributions and non-ideal surface properties can affect the emitted radiation.
Conclusion:
Wien’s displacement law is a crucial principle in the study of thermal radiation. It provides a mathematical expression for the spectral distribution of energy emitted by an object at different temperatures and has wide-ranging applications in fields such as astrophysics, thermal engineering, materials science, and climate science.
The law’s importance lies in its ability to describe the relationship between an object’s temperature and the wavelength of maximum radiation intensity emitted. This relationship allows for the determination of an object’s temperature based on the wavelength of its emitted radiation and is critical for understanding the properties and behavior of stars and other celestial bodies.
However, it is important to note that Wien’s displacement law applies only to ideal black bodies, and deviations from this ideal behavior must be taken into account in practical applications. Additionally, the law assumes that the emitted radiation is in thermal equilibrium with its surroundings, which is not always the case in real-world scenarios.
Overall, Wien’s displacement law is a crucial concept in thermal radiation and has numerous practical applications in many fields. Its importance in our understanding of the universe and its properties cannot be overstated, and its applications continue to shape our understanding of various phenomena.