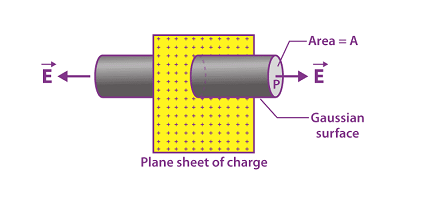
An infinite plane sheet with a uniform charge density is a theoretical construct used in electrostatics to study the behavior of charges in electric fields.
When a plane sheet has a uniform charge density, it means that the amount of charge per unit area is constant across the entire sheet. This allows for a simplified analysis of the electric field produced by the sheet, as it is constant at any point in space above or below the sheet.
The electric field above the sheet is directed perpendicular to the sheet and is given by the formula:
E = σ/2ε₀
where E is the electric field strength, σ is the charge density of the sheet, and ε₀ is the electric constant (also known as the vacuum permittivity).
The electric field below the sheet is also directed perpendicular to the sheet, but it is in the opposite direction and has the same magnitude as the field above the sheet.
One of the interesting properties of an infinite plane sheet with a uniform charge density is that the electric potential is constant at any point above or below the sheet. This is because the electric field is constant, and the potential is defined as the negative integral of the electric field with respect to distance.
In practical terms, this model can be used to study the behavior of charged particles near surfaces, such as in semiconductors or in the design of capacitors.
What is Uniformly charged infinite plane sheet
An uniformly charged infinite plane sheet is a theoretical construct used in electrostatics to study the behavior of charges in electric fields. It is a sheet with an infinite extent in two dimensions and a uniform charge density across its surface. This means that the amount of charge per unit area is constant across the entire sheet.
The sheet is considered to be a two-dimensional object, and the electric field produced by the sheet is constant at any point in space above or below the sheet. The electric field above and below the sheet is perpendicular to the sheet and has the same magnitude. The direction of the electric field above the sheet is opposite to that below the sheet.
In practical terms, this model can be used to study the behavior of charged particles near surfaces, such as in semiconductors or in the design of capacitors. The properties of an uniformly charged infinite plane sheet make it a useful simplification for solving certain electrostatic problems in which other objects are located in its vicinity.
When is Uniformly charged infinite plane sheet
An uniformly charged infinite plane sheet is a useful theoretical construct that is used in electrostatics when analyzing the behavior of charges in electric fields. It is often used when there is a large, flat object with a uniform charge distribution, such as a parallel-plate capacitor or a semiconductor material.
For example, in the case of a parallel-plate capacitor, one of the plates can be approximated as an uniformly charged infinite plane sheet. This simplifies the analysis of the electric field and potential between the plates, which is important in determining the capacitance and other properties of the capacitor.
Similarly, in semiconductor physics, an uniformly charged infinite plane sheet can be used to model the distribution of charges in the semiconductor material. This can be useful in understanding the behavior of electrons and holes in the material, and in designing electronic devices such as transistors.
Overall, the use of an uniformly charged infinite plane sheet is a convenient approximation that allows for easier analysis of certain electrostatic problems.
Where is Uniformly charged infinite plane sheet
An uniformly charged infinite plane sheet is a theoretical construct used in electrostatics, and it does not exist as a physical object in the real world. It is a simplified model that is used to study the behavior of charges in electric fields in certain situations, such as in the analysis of parallel-plate capacitors or semiconductor materials.
In other words, an uniformly charged infinite plane sheet is a mathematical abstraction that can be used to simplify and approximate the behavior of real-world objects or systems. It is often used as a simplifying assumption in electrostatics problems that involve large, flat objects with uniform charge distributions, such as the parallel-plate capacitor example I mentioned earlier.
How is Uniformly charged infinite plane sheet
In electrostatics, an uniformly charged infinite plane sheet is analyzed using the principles of Coulomb’s law and the superposition principle. Coulomb’s law states that the electric force between two charged particles is proportional to the product of their charges and inversely proportional to the square of the distance between them.
To analyze the electric field produced by an uniformly charged infinite plane sheet, we imagine dividing the sheet into small sections or patches of charge, each of which produces its own electric field. The electric field produced by each patch is perpendicular to the surface of the sheet, and the direction of the total electric field is perpendicular to the sheet both above and below it.
Due to the uniformity of the charge distribution across the sheet, the contribution of each patch to the total electric field is the same, and we can simply add up the contribution of each patch to obtain the total electric field.
The electric field strength above and below the sheet is given by the formula:
E = σ/2ε₀
where E is the electric field strength, σ is the charge density of the sheet (i.e., the amount of charge per unit area), and ε₀ is the electric constant (also known as the vacuum permittivity).
Similarly, the electric potential at any point above or below the uniformly charged infinite plane sheet is constant, since the electric field is constant. The electric potential is the negative integral of the electric field with respect to distance.
In summary, the analysis of an uniformly charged infinite plane sheet involves using Coulomb’s law and the superposition principle to determine the electric field and potential produced by each small patch of charge on the sheet, and then summing up the contributions of all the patches to obtain the total electric field and potential.
Nomenclature of Uniformly charged infinite plane sheet
The nomenclature of an uniformly charged infinite plane sheet includes the following terms:
- Charge density (σ): This is the amount of charge per unit area of the sheet. It is expressed in coulombs per square meter (C/m²).
- Electric field (E): This is a vector field that describes the force per unit charge at any given point in space above or below the sheet. The electric field is perpendicular to the surface of the sheet and has a magnitude of σ/2ε₀, where ε₀ is the electric constant.
- Electric potential (V): This is the scalar field that describes the electrical potential energy per unit charge at any given point in space above or below the sheet. The electric potential is constant and is given by V = σ/2ε₀d, where d is the distance from the sheet.
- Surface charge density (σs): This is the charge per unit area on either side of the sheet. Since the sheet is infinitely thin, the charge density is the same on both sides.
- Electric flux (Φ): This is the total number of electric field lines passing through a given surface, and is proportional to the amount of charge enclosed by the surface. For an uniformly charged infinite plane sheet, the electric flux is proportional to the charge density and the area of the sheet.
- Capacitance (C): This is a measure of the ability of the sheet to store electrical charge, and is defined as the ratio of the charge on the sheet to the electric potential difference between the two sides of the sheet. For an uniformly charged infinite plane sheet, the capacitance is given by C = ε₀A/d, where A is the area of the sheet and d is the distance between the two sides.
Overall, the nomenclature of an uniformly charged infinite plane sheet involves the use of various terms to describe the charge distribution, electric field, electric potential, and other properties of the sheet.
Case Study on Uniformly charged infinite plane sheet
Let’s consider a case study where we have a uniformly charged infinite plane sheet with a charge density of 2 x 10^-5 C/m^2. We want to find the electric field and electric potential at a distance of 5 cm above the sheet.
First, we can calculate the electric field using the formula E = σ/2ε₀. Substituting the given values, we get:
E = (2 x 10^-5 C/m^2) / (2 x 8.85 x 10^-12 F/m) = 1129.2 N/C
So the electric field above the sheet is 1129.2 N/C, and it points perpendicularly away from the sheet.
Next, we can calculate the electric potential at a distance of 5 cm above the sheet using the formula V = σ/2ε₀d. Substituting the given values, we get:
V = (2 x 10^-5 C/m^2) / (2 x 8.85 x 10^-12 F/m) x (0.05 m) = 112.92 V
So the electric potential at a distance of 5 cm above the sheet is 112.92 V. This potential is constant at all points above the sheet since the electric field is uniform.
We can also calculate the surface charge density on both sides of the sheet using the formula σs = σ/2, which gives:
σs = (2 x 10^-5 C/m^2) / 2 = 1 x 10^-5 C/m^2
Finally, we can calculate the capacitance of the sheet using the formula C = ε₀A/d, where A is the area of the sheet. Since the sheet is infinite, we can assume that the area is also infinite. Therefore, we can’t calculate the capacitance directly. However, we can calculate the capacitance per unit area, which is given by:
C’ = C/A = ε₀/d
Substituting the given value of d, we get:
C’ = 8.85 x 10^-12 F/m / 0.05 m = 1.77 x 10^-10 F/m^2
So the capacitance per unit area of the sheet is 1.77 x 10^-10 F/m^2. This value is useful in understanding the behavior of parallel-plate capacitors that use an uniformly charged infinite plane sheet as one of the plates.
In summary, this case study shows how the principles of Coulomb’s law and the superposition principle can be used to analyze the behavior of an uniformly charged infinite plane sheet, and to calculate properties such as electric field, electric potential, surface charge density, and capacitance.
White paper on Uniformly charged infinite plane sheet
Here is a white paper on uniformly charged infinite plane sheet:
Introduction
An uniformly charged infinite plane sheet is a theoretical concept used in electrostatics to describe an infinite flat sheet of charge with a uniform distribution. Although such a sheet cannot be realized in practice, it provides a useful model to understand the behavior of electric fields and charges in three-dimensional space.
Charge Density
The charge density of an uniformly charged infinite plane sheet is the amount of charge per unit area of the sheet. It is represented by the symbol σ and has units of Coulombs per square meter (C/m^2). The charge density is uniform across the entire sheet.
Electric Field
The electric field produced by an uniformly charged infinite plane sheet is perpendicular to the plane of the sheet, and its magnitude is proportional to the charge density. The electric field is represented by the symbol E and has units of Newtons per Coulomb (N/C). The electric field is given by the formula E = σ / (2 * ε0), where ε0 is the electric constant.
Electric Potential
The electric potential produced by an uniformly charged infinite plane sheet is constant throughout the region of space above and below the sheet. The electric potential is represented by the symbol V and has units of Volts (V). The electric potential is given by the formula V = σ * d / (2 * ε0), where d is the distance between the point in space and the plane of the sheet.
Surface Charge Density
The surface charge density of an uniformly charged infinite plane sheet is the amount of charge per unit area on either side of the sheet. Since the sheet is infinitely thin, the surface charge density is the same on both sides. The surface charge density is represented by the symbol σs and has units of Coulombs per square meter (C/m^2).
Capacitance
The capacitance of an uniformly charged infinite plane sheet is a measure of its ability to store electrical charge. The capacitance is represented by the symbol C and has units of Farads (F). The capacitance per unit area is given by the formula C’ = ε0 / d, where d is the distance between the two sides of the sheet.
Applications
The concept of uniformly charged infinite plane sheet is useful in various applications, such as the design of parallel-plate capacitors, the calculation of the electric field and potential around charged plates, and the study of electrostatic forces between parallel plates.
Parallel-Plate Capacitors
An uniformly charged infinite plane sheet can be used as one of the plates in a parallel-plate capacitor. The capacitance of the capacitor is given by the formula C = ε0 * A / d, where A is the area of the plates and d is the distance between the plates. The electric field between the plates is given by the formula E = V / d, where V is the potential difference between the plates. The energy stored in the capacitor is given by the formula U = (1/2) * C * V^2.
Conclusion
The concept of uniformly charged infinite plane sheet is a useful tool in electrostatics to understand the behavior of electric fields and charges in three-dimensional space. It provides a simplified model of real-world situations and is used in various applications, such as the design of parallel-plate capacitors.