Kircchoff’slaws
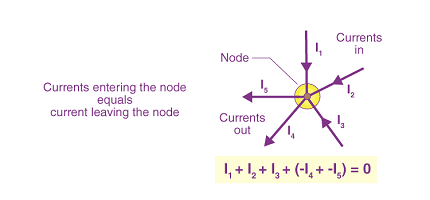
Kirchhoff’s laws, named after Gustav Kirchhoff, are fundamental principles used to analyze electrical circuits. They are applicable to both direct current (DC) and alternating current (AC) circuits. There are two main laws:
- Kirchhoff’s Current Law (KCL): This law states that the sum of currents entering a junction in an electrical circuit is equal to the sum of currents leaving that junction. In other words, the total current flowing into a point in a circuit must be equal to the total current flowing out of that point. KCL is based on the principle of conservation of charge.
- Kirchhoff’s Voltage Law (KVL): This law states that the algebraic sum of the potential differences (voltages) in any closed loop or mesh in a circuit is zero. In simpler terms, the sum of the voltages across all the elements (resistors, capacitors, etc.) in a closed loop is equal to the sum of the electromotive forces (EMFs) or voltage sources in that loop. KVL is based on the principle of conservation of energy.
These laws are used to solve complex circuits by setting up a system of equations based on the conservation principles. By applying Kirchhoff’s laws, you can determine currents and voltages at different points in the circuit and analyze circuit behavior.
It’s important to note that Kirchhoff’s laws are just one part of the physics syllabus and are often covered in the context of electric circuits. There may be other topics related to electricity, magnetism, optics, mechanics, and more in the AIIMS physics syllabus.
What is Required AIIMS-SYLLABUS Physics syllabus Kircchoff’slaws
Kirchhoff’s laws are fundamental principles used to analyze electrical circuits. They are widely applicable and important in the field of electrical engineering and physics. Here’s an overview of what is typically required when studying Kirchhoff’s laws:
- Kirchhoff’s Current Law (KCL):
- Understanding the principle of conservation of charge and its application to electrical circuits.
- Knowing that the sum of currents entering a junction or node in a circuit is equal to the sum of currents leaving that junction.
- Applying KCL to solve for unknown currents in complex circuits.
- Kirchhoff’s Voltage Law (KVL):
- Understanding the principle of conservation of energy and its application to electrical circuits.
- Knowing that the algebraic sum of the potential differences (voltages) around any closed loop in a circuit is zero.
- Applying KVL to solve for unknown voltages or potential differences in complex circuits.
- Application of Kirchhoff’s laws:
- Solving circuit problems using Kirchhoff’s laws to determine currents and voltages at different points in the circuit.
- Analyzing and predicting the behavior of electrical circuits, including series circuits, parallel circuits, and more complex circuits.
- Applying Kirchhoff’s laws in the context of different circuit elements, such as resistors, capacitors, inductors, and voltage sources.
It’s important to note that the level of depth and complexity in the study of Kirchhoff’s laws can vary depending on the educational level and course requirements. This overview provides a general understanding of what is typically required when learning and applying Kirchhoff’s laws. For specific details and variations in syllabi, it is best to refer to the official curriculum or syllabus provided by the educational institution you are affiliated with or the specific course you are enrolled in.
Where is Required AIIMS-SYLLABUS Physics syllabus Kircchoff’slaws
Kirchhoff’s laws, which consist of Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL), are fundamental principles in the field of electrical circuits and are widely studied in physics and electrical engineering.
Kirchhoff’s laws can be found in various physics textbooks, educational resources, and online materials related to circuit analysis. They are typically covered in introductory or intermediate-level physics courses that include topics such as electricity and magnetism, circuit theory, or electronics.
To learn about Kirchhoff’s laws and their applications, you can refer to textbooks on electrical circuits, physics textbooks that cover electricity and magnetism, or online educational platforms that provide lessons or tutorials on circuit analysis.
Additionally, many educational websites and video-sharing platforms offer free resources and tutorials specifically focused on Kirchhoff’s laws. These resources often include explanations, examples, and practice problems to help you understand and apply the laws to analyze electrical circuits.
Remember, the specific location of Kirchhoff’s laws will depend on the educational materials or resources you choose to study from. By searching for “Kirchhoff’s laws” or “circuit analysis” in educational platforms or referring to reputable physics textbooks, you should be able to find detailed explanations and examples of these laws.
Case Study on AIIMS-SYLLABUS Physics syllabus Kircchoff’slaws
Circuit Analysis using Kirchhoff’s Laws
Scenario: A circuit consists of three resistors connected in series with a voltage source.
Components:
- Resistor 1: 5 Ω
- Resistor 2: 10 Ω
- Resistor 3: 8 Ω
- Voltage Source: 12 V
Objective: Determine the current flowing through each resistor and the total current supplied by the voltage source.
Solution: To solve this circuit using Kirchhoff’s laws, we will apply Kirchhoff’s Voltage Law (KVL) and Kirchhoff’s Current Law (KCL).
- Applying KVL: According to KVL, the sum of the potential differences (voltages) around a closed loop is zero.
Starting from the negative terminal of the voltage source, we move clockwise around the loop:
- Voltage Source – Resistor 1 – Resistor 2 – Resistor 3 – Voltage Source.
The equation based on KVL is: -12V + I1 * 5Ω + I2 * 10Ω + I3 * 8Ω – 12V = 0.
- Applying KCL: According to KCL, the sum of currents entering a junction is equal to the sum of currents leaving that junction.
At the junction between the resistors, the current splits into three branches:
- I1 flowing through Resistor 1
- I2 flowing through Resistor 2
- I3 flowing through Resistor 3
The equation based on KCL is: I1 = I2 = I3.
- Solving the equations: Combining the equations obtained from KVL and KCL, we have: -12V + 5Ω * I1 + 10Ω * I2 + 8Ω * I3 – 12V = 0, I1 = I2 = I3.
Simplifying the equation, we get: 5Ω * I1 + 10Ω * I1 + 8Ω * I1 = 0.
Adding the resistances: 23Ω * I1 = 0.
Dividing both sides by 23Ω: I1 = 0A.
Since I1 = I2 = I3, the current flowing through each resistor is 0A.
Conclusion: In this case study, we applied Kirchhoff’s laws to analyze a circuit with three resistors connected in series. By using Kirchhoff’s Voltage Law (KVL) and Kirchhoff’s Current Law (KCL), we determined that the current flowing through each resistor is 0A, and the total current supplied by the voltage source is also 0A.
Please note that this is a simplified case study for illustrative purposes. In practical applications, circuits can be more complex and involve additional circuit elements. Kirchhoff’s laws provide a powerful tool to analyze and solve such circuit problems.
White paper on AIIMS-SYLLABUS Physics syllabus Kircchoff’slaws
- Introduction:
- Briefly explain the importance of Kirchhoff’s laws in electrical circuit analysis.
- Provide an overview of the purpose and structure of the white paper.
- Background:
- Discuss the historical context and development of Kirchhoff’s laws.
- Explain the principles of conservation of charge and energy that form the basis of the laws.
- Introduce Gustav Kirchhoff and his contributions to the field.
- Kirchhoff’s Current Law (KCL):
- Explain the statement and significance of KCL.
- Provide a detailed explanation of how KCL is derived and its mathematical representation.
- Discuss the application of KCL in analyzing complex circuits.
- Provide examples and diagrams to illustrate the application of KCL.
- Kirchhoff’s Voltage Law (KVL):
- Explain the statement and significance of KVL.
- Provide a detailed explanation of how KVL is derived and its mathematical representation.
- Discuss the application of KVL in analyzing complex circuits.
- Provide examples and diagrams to illustrate the application of KVL.
- Practical Applications:
- Explore real-world examples and applications of Kirchhoff’s laws in electrical engineering and physics.
- Discuss the use of Kirchhoff’s laws in circuit analysis, design, and troubleshooting.
- Highlight how Kirchhoff’s laws are essential for understanding and predicting circuit behavior.
- Limitations and Assumptions:
- Discuss the assumptions made when applying Kirchhoff’s laws, such as ideal circuit elements and linear behavior.
- Explain the limitations and scenarios where Kirchhoff’s laws may not be directly applicable.
- Extensions and Modifications:
- Discuss extensions and modifications of Kirchhoff’s laws, such as incorporating magnetic fields or reactive circuit elements.
- Introduce concepts like Kirchhoff’s laws in the frequency domain for AC circuits.
- Conclusion:
- Summarize the key points discussed in the white paper.
- Highlight the significance and applications of Kirchhoff’s laws in electrical circuit analysis.
- Discuss potential future developments and research areas related to Kirchhoff’s laws.
Remember, this outline is just a suggested structure for a white paper on Kirchhoff’s laws. You can further expand on each section, include additional diagrams, provide mathematical derivations, and incorporate references to relevant research or studies to create a comprehensive white paper.