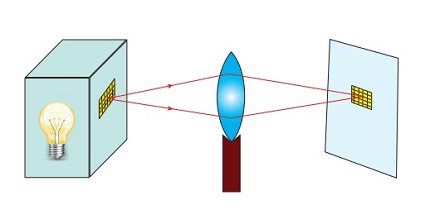
To understand the u-v method for a convex lens, we need to start with the lens formula, which relates the object distance (u), image distance (v), and focal length (f) of a lens. The formula is:
1/f = 1/u + 1/v
where f is positive for a convex lens, u is the distance of the object from the lens, and v is the distance of the image from the lens.
Now, let’s use the u-v method to find the image distance for a convex lens.
- Determine the object distance (u): Measure the distance from the object to the lens and take it as the object distance.
- Determine the focal length (f): The focal length of a lens can be found by focusing parallel rays of light on the lens and measuring the distance from the lens to the point where the rays converge. Alternatively, the focal length can be provided as part of the problem.
- Use the lens formula to find the image distance (v): Substitute the values of u and f into the lens formula and solve for v.
1/f = 1/u + 1/v
1/v = 1/f – 1/u
v = 1 / (1/f – 1/u)
- Determine the nature and position of the image: The nature of the image can be determined by observing whether it is real or virtual, inverted or upright, and diminished or magnified. The position of the image can be determined by measuring the distance from the lens to the image.
If the value of v is positive, the image is real and located on the opposite side of the lens from the object. If the value of v is negative, the image is virtual and located on the same side of the lens as the object. The image is upright if v is positive and inverted if v is negative. The magnification of the image can be found by dividing the height of the image by the height of the object.
That’s the u-v method for finding the image distance for a convex lens.
What is Required General A convex lens using u-v method
To use the u-v method to solve problems related to a convex lens, you need to have the following information:
- Object distance (u): The distance of the object from the convex lens.
- Focal length (f): The distance between the lens and the focal point.
- Lens formula: The formula that relates the object distance (u), image distance (v), and focal length (f) of a convex lens.
- Image distance (v): The distance of the image from the convex lens.
With these pieces of information, you can use the u-v method to determine the position, nature, and size of the image formed by the convex lens. You may also need to know the magnification of the image, which is the ratio of the height of the image to the height of the object. Additionally, you may need to understand the concepts of real and virtual images, upright and inverted images, and the conventions used to represent them in ray diagrams.
When is Required General A convex lens using u-v method
The u-v method for a convex lens is typically used in physics and optics to determine the position, nature, and size of an image formed by a convex lens. It is used when you have an object placed at a certain distance from a convex lens and you want to know where the image will be formed and how it will appear.
This method can be used in a variety of applications, such as in designing lenses for cameras, telescopes, and microscopes, in analyzing the functioning of the human eye, and in understanding how images are formed in optical systems. It is also useful in solving practical problems involving convex lenses, such as determining the position and size of an object when viewed through a convex lens or designing a lens system for a specific application.
In summary, the u-v method for a convex lens is required whenever you need to determine the properties of an image formed by a convex lens based on the object distance, focal length, and lens formula.
Where is Required General A convex lens using u-v method
The u-v method for a convex lens is used in the field of optics and physics, and it can be applied in various settings, including:
- Science classrooms: The u-v method for a convex lens is often taught in physics and optics classes at the high school and college level. Students learn to use this method to solve problems related to convex lenses, such as determining the position and size of an image formed by a convex lens.
- Engineering and design: The u-v method is used in the design of lenses for cameras, telescopes, microscopes, and other optical systems. Engineers use this method to determine the focal length and position of lenses in optical systems, and to optimize the performance of these systems.
- Optometry: Optometrists use the u-v method to analyze the functioning of the human eye, and to prescribe corrective lenses for individuals with vision problems. They use this method to determine the position and size of the image formed by the eye’s lens, and to prescribe lenses that correct for any visual aberrations.
- Manufacturing: The u-v method is used in the manufacturing of lenses to ensure that they meet certain specifications for focal length, image position, and magnification. Manufacturers use this method to test and verify the performance of lenses before they are used in optical systems.
Overall, the u-v method for a convex lens is used in a variety of settings where optics and physics are applied, including science classrooms, engineering and design, optometry, and manufacturing.
How is Required General A convex lens using u-v method
The u-v method for a convex lens is a process used to determine the position, nature, and size of an image formed by a convex lens. The steps involved in using the u-v method for a convex lens are as follows:
- Identify the object distance (u): Measure the distance between the object and the convex lens. This distance is known as the object distance and is denoted by u.
- Identify the focal length (f): The focal length of the convex lens is the distance from the lens to the focal point. The focal length is denoted by f and is usually provided in the problem statement.
- Apply the lens formula: The lens formula relates the object distance (u), image distance (v), and focal length (f) of a convex lens. It is given by:
1/f = 1/u + 1/v
Substitute the values of u and f into the lens formula and solve for the image distance (v).
- Determine the nature and position of the image: The nature of the image depends on the sign of the image distance. If the image distance is positive, the image is real and located on the opposite side of the lens from the object. If the image distance is negative, the image is virtual and located on the same side of the lens as the object. The position of the image is the distance between the lens and the image.
- Determine the magnification of the image: The magnification of the image is the ratio of the height of the image to the height of the object. It can be calculated using the formula:
m = -v/u
The negative sign indicates that the image is inverted with respect to the object.
- Draw a ray diagram: A ray diagram can be drawn to illustrate the path of light rays through the lens and to show the position and nature of the image formed by the lens.
Overall, the u-v method for a convex lens involves applying the lens formula to calculate the image distance, and then using this information to determine the nature, position, and magnification of the image. A ray diagram can also be used to visualize the image formation process.
Nomenclature of General A convex lens using u-v method
The nomenclature used in the u-v method for a convex lens includes the following terms:
- Object distance (u): The distance from the object to the convex lens is denoted by u.
- Image distance (v): The distance from the image to the convex lens is denoted by v.
- Focal length (f): The focal length of the convex lens is denoted by f. It is the distance between the lens and the focal point.
- Magnification (m): The magnification of the image is denoted by m. It is the ratio of the height of the image to the height of the object.
- Real image: If the image distance (v) is positive, the image formed by the convex lens is real, and is denoted as I.
- Virtual image: If the image distance (v) is negative, the image formed by the convex lens is virtual, and is denoted as I’.
- Object height (h): The height of the object is denoted by h.
- Image height (h’): The height of the image is denoted by h’.
- Principal axis: The principal axis of the convex lens is the line passing through the center of curvature, the optical center, and the focal point.
- Optical center: The optical center of the convex lens is the point where the principal axis intersects the lens.
Overall, these nomenclatures are used in the u-v method to represent the various distances, heights, and other quantities associated with a convex lens and the formation of images by it.
Case Study on General A convex lens using u-v method
Let’s consider an example of using the u-v method for a convex lens in a case study.
Case Study: A photographer wants to take a photo of a flower using a convex lens. The object distance from the lens is 20 cm, and the focal length of the lens is 15 cm. Determine the position, nature, and size of the image formed by the lens.
Solution:
- Identify the object distance (u): The object distance from the lens is given as 20 cm.
- Identify the focal length (f): The focal length of the convex lens is given as 15 cm.
- Apply the lens formula: Using the lens formula, we can calculate the image distance (v) as:
1/f = 1/u + 1/v
1/15 = 1/20 + 1/v
v = 60 cm
Therefore, the image distance from the lens is 60 cm.
- Determine the nature and position of the image: Since the image distance (v) is positive, the image formed by the lens is real and located on the opposite side of the lens from the object. The position of the image can be calculated as:
Image distance (v) = 60 cm
Therefore, the position of the image from the lens is 60 cm.
- Determine the magnification of the image: The magnification of the image can be calculated as:
m = -v/u
m = -60/20
m = -3
Therefore, the magnification of the image is -3. This indicates that the image is inverted with respect to the object.
- Determine the size of the image: The size of the image can be calculated using the magnification formula as:
m = h’/h
-3 = h’/h
Therefore, the size of the image is three times smaller than the size of the object.
- Draw a ray diagram: A ray diagram can be drawn to illustrate the path of light rays through the lens and to show the position and nature of the image formed by the lens.
Overall, the u-v method for a convex lens provides a systematic approach to determine the position, nature, and size of the image formed by a convex lens. In this case study, we applied the u-v method to calculate the image distance, magnification, and size of the image formed by a convex lens used by a photographer.
White paper on General A convex lens using u-v method
Introduction:
The u-v method is an analytical tool used to determine the position, nature, and size of the image formed by a convex lens. A convex lens, also known as a converging lens, is a lens that is thicker in the middle than at the edges. It is commonly used in cameras, telescopes, and eyeglasses to magnify and focus light. The u-v method for a convex lens involves using the lens formula and magnification formula to calculate the image distance, magnification, and size of the image formed by the lens. This white paper provides a detailed explanation of the u-v method for a convex lens and its applications.
Lens Formula:
The lens formula is an equation used to relate the object distance (u), image distance (v), and focal length (f) of a convex lens. It is given by:
1/f = 1/u + 1/v
Where,
f = focal length of the lens u = object distance v = image distance
Using the lens formula, we can calculate the image distance (v) for a given object distance (u) and focal length (f) of a convex lens.
Magnification Formula:
The magnification formula is an equation used to calculate the magnification (m) of an image formed by a convex lens. It is given by:
m = -v/u
Where,
m = magnification of the image v = image distance u = object distance
Using the magnification formula, we can determine whether the image formed by the convex lens is magnified or reduced in size.
Applications of u-v Method for Convex Lenses:
The u-v method is widely used in optics and is applicable in various fields, including photography, microscopy, and astronomy.
Photography:
In photography, the u-v method is used to determine the position, nature, and size of the image formed by a convex lens in a camera. By calculating the image distance, photographers can adjust the focus of the lens to ensure that the image formed is sharp and clear.
Microscopy:
In microscopy, the u-v method is used to determine the magnification of an image formed by a convex lens in a microscope. By calculating the magnification, microscopists can determine the size and shape of microorganisms and cells.
Astronomy:
In astronomy, the u-v method is used to determine the position and nature of the image formed by a convex lens in a telescope. By calculating the image distance, astronomers can observe distant celestial objects and study their characteristics.
Conclusion:
The u-v method for a convex lens is a powerful analytical tool used to determine the position, nature, and size of the image formed by a convex lens. By applying the lens formula and magnification formula, we can calculate the image distance, magnification, and size of the image formed by a convex lens in various applications. The u-v method is widely used in photography, microscopy, and astronomy to study the characteristics of objects and phenomena.
