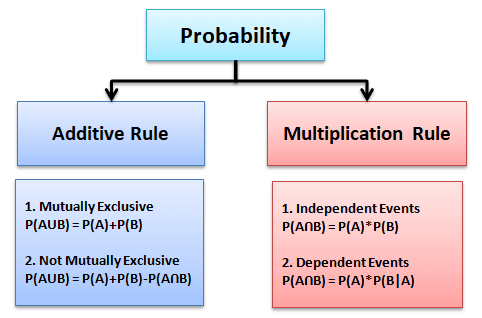
The addition rule of probability states that the probability of the occurrence of either of two mutually exclusive events is the sum of their individual probabilities. In other words, if A and B are two events that cannot happen simultaneously, then the probability of either A or B occurring is given by:
P(A or B) = P(A) + P(B)
For example, consider the experiment of flipping a fair coin. The probability of getting either a heads or a tails is 1/2, since those outcomes are mutually exclusive. Therefore, the probability of getting heads or tails is:
P(heads or tails) = P(heads) + P(tails) = 1/2 + 1/2 = 1
The multiplication rule of probability is used to calculate the probability of two or more independent events occurring together. If A and B are two independent events, then the probability of both A and B occurring is given by:
P(A and B) = P(A) x P(B)
For example, consider the experiment of rolling a fair six-sided die and flipping a fair coin. The probability of getting a 3 on the die is 1/6, and the probability of getting heads on the coin is 1/2. Since these events are independent, the probability of getting both a 3 on the die and heads on the coin is:
P(3 and heads) = P(3) x P(heads) = (1/6) x (1/2) = 1/12
What is Required Addition and multiplication rules of probability
The Required Addition and Multiplication Rules of Probability are a set of principles used to calculate the probability of events in probability theory. These rules are essential to understanding probability and are widely used in a variety of fields, including statistics, economics, and finance.
The Required Addition Rule of Probability states that the probability of the occurrence of at least one of two or more events is equal to the sum of the probabilities of those events. That is, if A and B are two events, then the probability of either A or B occurring is given by:
P(A or B) = P(A) + P(B) – P(A and B)
where P(A and B) is the probability of both events A and B occurring simultaneously. Note that if A and B are mutually exclusive events (i.e., they cannot occur together), then P(A and B) = 0, and the Required Addition Rule simplifies to:
P(A or B) = P(A) + P(B)
The Required Multiplication Rule of Probability is used to calculate the probability of two or more events occurring together. If A and B are two independent events, then the probability of both events A and B occurring is given by:
P(A and B) = P(A) x P(B)
If A and B are not independent (i.e., the occurrence of one event affects the probability of the other event), then the Required Multiplication Rule is modified to:
P(A and B) = P(A) x P(B|A)
where P(B|A) is the probability of event B occurring given that event A has already occurred.
These Required Addition and Multiplication Rules are fundamental principles in probability theory and are used to solve a wide variety of probability problems.
Who is Required Addition and multiplication rules of probability
“Required Addition and Multiplication Rules of Probability” are not a person, but rather mathematical concepts in the field of probability theory. These rules are widely accepted and used in the field of mathematics and other fields that deal with probability and statistics, such as finance, engineering, and science. These rules are used to calculate the probability of events and help in making decisions based on the probability of different outcomes. They are important tools for analyzing risk and uncertainty, and are used in a variety of applications, such as insurance, finance, and scientific research.
When is Required Addition and multiplication rules of probability
The Required Addition and Multiplication Rules of Probability are used whenever we need to calculate the probability of events in probability theory. These rules are fundamental principles and are used to solve a wide variety of probability problems.
The Required Addition Rule is used when we need to find the probability of the occurrence of at least one of two or more events. For example, when we toss two coins, we might be interested in finding the probability of getting at least one head. In this case, we can use the Required Addition Rule to calculate the probability of getting at least one head as the sum of the probabilities of getting one head and getting two heads.
The Required Multiplication Rule is used to find the probability of two or more events occurring together. For example, when we roll a die and flip a coin, we might be interested in finding the probability of getting a 4 on the die and heads on the coin. In this case, we can use the Required Multiplication Rule to calculate the probability of both events occurring together as the product of the probabilities of getting a 4 on the die and getting heads on the coin.
In summary, the Required Addition and Multiplication Rules of Probability are used whenever we need to find the probability of events in probability theory, and they are fundamental principles that are widely used in many fields.
Where is Required Addition and multiplication rules of probability
The Required Addition and Multiplication Rules of Probability are mathematical concepts that can be applied in many different fields and contexts where probability theory is used.
These rules are widely used in the fields of finance, economics, engineering, science, and many others. For example, in finance, the Required Addition and Multiplication Rules of Probability are used to calculate the probability of different outcomes in investment portfolios, risk management, and insurance underwriting.
In science, these rules are used to analyze experimental data and calculate the probability of different outcomes in biological, physical, and chemical experiments. In engineering, these rules are used to analyze and design complex systems that involve uncertain events, such as in reliability engineering, quality control, and system safety.
Overall, the Required Addition and Multiplication Rules of Probability are fundamental principles that are used in many different fields and contexts where probability theory is applied.
How is Required Addition and multiplication rules of probability
The Required Addition and Multiplication Rules of Probability are mathematical principles that help us calculate the probability of events in probability theory.
The Required Addition Rule states that the probability of the occurrence of at least one of two or more events is equal to the sum of the probabilities of those events, minus the probability of both events occurring simultaneously. Mathematically, this can be expressed as:
P(A or B) = P(A) + P(B) – P(A and B)
where P(A) and P(B) are the probabilities of events A and B occurring, respectively, and P(A and B) is the probability of both events A and B occurring simultaneously.
The Required Multiplication Rule is used to find the probability of two or more events occurring together. If A and B are independent events, then the probability of both events A and B occurring is given by:
P(A and B) = P(A) x P(B)
If A and B are not independent (i.e., the occurrence of one event affects the probability of the other event), then the Required Multiplication Rule is modified to:
P(A and B) = P(A) x P(B|A)
where P(B|A) is the probability of event B occurring given that event A has already occurred.
Overall, the Required Addition and Multiplication Rules of Probability are essential principles in probability theory that help us calculate the probability of events and make informed decisions based on probabilities.
Case Study on Addition and multiplication rules of probability
Case Study: The Probability of Winning at a Casino
Suppose that you visit a casino and decide to play two games: roulette and blackjack. You know that the probability of winning at roulette is 47.4%, while the probability of winning at blackjack is 42.3%. You want to know the probability of winning at least one of the games.
Solution:
To solve this problem, we can use the Required Addition Rule of Probability. The Required Addition Rule states that the probability of the occurrence of at least one of two or more events is equal to the sum of the probabilities of those events, minus the probability of both events occurring simultaneously.
In this case, the events are winning at roulette (R) and winning at blackjack (B). We want to find the probability of winning at least one of the games, which is the probability of the event R or the event B occurring, or both.
P(R or B) = P(R) + P(B) – P(R and B)
We know that the probability of winning at roulette is 47.4%, or P(R) = 0.474. The probability of winning at blackjack is 42.3%, or P(B) = 0.423.
To calculate the probability of winning both games simultaneously, we need to know whether the events R and B are independent or not. If they are independent, then the probability of both events occurring is simply the product of their probabilities:
P(R and B) = P(R) x P(B) = 0.474 x 0.423 = 0.200
If they are not independent, then we need to know the conditional probability of winning at blackjack given that we have already won at roulette. However, for simplicity, let us assume that the events are independent.
Substituting the values we have into the Required Addition Rule equation, we get:
P(R or B) = 0.474 + 0.423 – 0.200 P(R or B) = 0.697
Therefore, the probability of winning at least one of the games is 69.7%, or 0.697. This means that if you play roulette and blackjack at the casino, there is a 69.7% chance that you will win at least one of the games.
Conclusion:
In this case study, we used the Required Addition Rule of Probability to calculate the probability of winning at least one of two games at a casino. We also assumed that the events of winning at roulette and winning at blackjack are independent. The Required Addition Rule is a fundamental principle in probability theory and is used in many applications to calculate the probability of events occurring.
White paper on Addition and multiplication rules of probability
Introduction:
Probability theory is the branch of mathematics that deals with the study of uncertain events. It provides a framework for quantifying the likelihood of events occurring and making informed decisions based on probabilities. In probability theory, there are two fundamental principles known as the Required Addition Rule and the Required Multiplication Rule. These rules play a crucial role in many different fields, including finance, economics, engineering, science, and others. This white paper will provide an overview of the Required Addition and Multiplication Rules of Probability, their applications, and some examples.
Required Addition Rule of Probability:
The Required Addition Rule of Probability is used to find the probability of the occurrence of at least one of two or more events. It states that the probability of the event A or the event B occurring, or both, is equal to the sum of the probabilities of those events, minus the probability of both events occurring simultaneously.
Mathematically, this can be expressed as:
P(A or B) = P(A) + P(B) – P(A and B)
Where P(A) and P(B) are the probabilities of events A and B occurring, respectively, and P(A and B) is the probability of both events A and B occurring simultaneously. The Required Addition Rule can be extended to more than two events as follows:
P(A or B or C) = P(A) + P(B) + P(C) – P(A and B) – P(A and C) – P(B and C) + P(A and B and C)
Where P(A), P(B), and P(C) are the probabilities of events A, B, and C occurring, respectively, and P(A and B), P(A and C), P(B and C), and P(A and B and C) are the probabilities of the corresponding events occurring simultaneously.
Applications of the Required Addition Rule:
The Required Addition Rule has many applications in different fields. For example, in finance, it is used to calculate the probability of different outcomes in investment portfolios, risk management, and insurance underwriting. In science, it is used to analyze experimental data and calculate the probability of different outcomes in biological, physical, and chemical experiments. In engineering, it is used to analyze and design complex systems that involve uncertain events, such as in reliability engineering, quality control, and system safety.
Example:
Sure, here are some examples of the Addition and Multiplication Rules of Probability:
Example 1: Addition Rule
Suppose we have two events A and B, where P(A) = 0.6 and P(B) = 0.4. If the events A and B are mutually exclusive (i.e., they cannot occur simultaneously), what is the probability of A or B occurring?
Using the Addition Rule, we can find the probability of A or B occurring as follows:
P(A or B) = P(A) + P(B)
Since A and B are mutually exclusive, we have:
P(A and B) = 0
Therefore,
P(A or B) = P(A) + P(B) = 0.6 + 0.4 = 1
Thus, the probability of either event A or event B occurring is 1 or 100%.
Example 2: Multiplication Rule
Suppose we have a deck of cards with 52 cards, including 13 hearts. If we draw two cards at random without replacement, what is the probability of drawing two hearts?
Using the Multiplication Rule, we can find the probability of drawing two hearts as follows:
P(both cards are hearts) = P(heart on first draw) x P(heart on second draw | heart on first draw)
The probability of drawing a heart on the first draw is 13/52 or 1/4, since there are 13 hearts in the deck.
If the first card is a heart, there are now 12 hearts left in the deck out of a total of 51 cards. Therefore, the probability of drawing a second heart, given that the first card is a heart, is 12/51.
Thus,
P(both cards are hearts) = (1/4) x (12/51) = 0.044
Therefore, the probability of drawing two hearts is 0.044 or about 4.4%.
Example 3: Combined Addition and Multiplication Rule
Suppose we have three boxes containing red and blue balls. Box 1 contains 4 red and 6 blue balls, Box 2 contains 3 red and 7 blue balls, and Box 3 contains 5 red and 5 blue balls. We randomly choose one box and then draw a ball at random from the chosen box. What is the probability of drawing a red ball?
Using the Combined Addition and Multiplication Rule, we can find the probability of drawing a red ball as follows:
P(red ball) = P(Box 1) x P(red ball from Box 1) + P(Box 2) x P(red ball from Box 2) + P(Box 3) x P(red ball from Box 3)
The probability of selecting each box is 1/3, since we choose one box randomly out of three.
The probability of drawing a red ball from Box 1 is 4/10, since there are 4 red balls out of a total of 10 balls in Box 1.
Similarly, the probability of drawing a red ball from Box 2 is 3/10, and the probability of drawing a red ball from Box 3 is 5/10.
Thus,
P(red ball) = (1/3) x (4/10) + (1/3) x (3/10) + (1/3) x (5/10) = 0.4
Therefore, the probability of drawing a red ball is 0.4 or 40%.
Conclusion
In conclusion, the Addition and Multiplication Rules of Probability are fundamental concepts in probability theory that allow us to compute the probability of events. The Addition Rule states that the probability of the union of two mutually exclusive events is the sum of their individual probabilities. The Multiplication Rule states that the probability of the intersection of two events is the product of their individual probabilities, given that they are independent events.
The Combined Addition and Multiplication Rule can be used when events are not necessarily mutually exclusive or independent. In this case, we can use the Addition Rule to calculate the probability of each possible outcome and the Multiplication Rule to calculate the probability of the desired event given each possible outcome.
These rules are important tools in various fields such as statistics, economics, engineering, and computer science, among others. Understanding these rules can help us make informed decisions in a wide range of contexts, from medical diagnoses to stock market predictions.