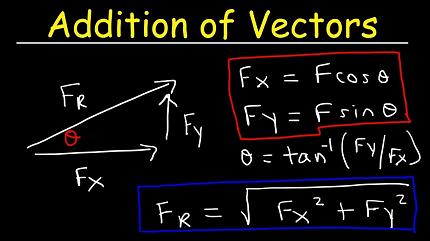
To add two vectors, you need to add their corresponding components. If you have two vectors, A and B, both with three components (x, y, z), then you can add them as follows:
A + B = (Ax + Bx, Ay + By, Az + Bz)
In other words, to add two vectors, you simply add their x-components, their y-components, and their z-components separately. This works for vectors with any number of components, as long as the two vectors being added have the same number of components.
Note that the result of vector addition is itself a vector. The magnitude and direction of the resulting vector can be calculated using the Pythagorean theorem and trigonometry, respectively.
Vector (mathematics and physics)
In science and physical science, vector is a term that alludes casually to certain amounts that can’t be communicated by a solitary number (a scalar), or to components of some vector spaces.
By and large, vectors were presented in calculation and material science (ordinarily in mechanics) for amounts that have both an extent and a course, like relocations, powers and speed. Such amounts are addressed by mathematical vectors similarly as distances, masses and time are addressed by genuine numbers.
The term vector is likewise utilized, in certain specific circumstances, for tuples, which are limited successions of quantities of a decent length.
Both mathematical vectors and tuples can be added and scaled, and these vector tasks prompted the idea of a vector space, which is a set outfitted with a vector option and a scalar duplication that fulfill a few maxims summing up the principal properties of procedure on the above kinds of vectors. A vector space framed by mathematical vectors is known as an Euclidean vector space, and a vector space shaped by tuples is known as a direction vector space.
Numerous vector spaces are viewed as in math, for example, expansion field, polynomial rings, algebras and capability spaces. The term vector is for the most part not utilized for components of these vectors spaces, and is by and large held for mathematical vectors, tuples, and components of unknown vector spaces (for instance, while examining general properties of vector spaces).
Vectors in Euclidean geometry
In science, physical science, and designing, an Euclidean vector or just a vector (in some cases called a mathematical vector or spatial vector) is a mathematical item that has greatness (or length) and bearing. Vectors can be added to different vectors as indicated by vector variable based math. An Euclidean vector is often addressed by a coordinated line fragment, or graphically as a bolt interfacing an underlying point A with a terminal point B, and meant by

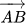
A vector is expected to “convey” the point A to the point B; the Latin word vector signifies “carrier”. It was first utilized by eighteenth century stargazers exploring planetary insurgency around the Sun. The greatness of the vector is the distance between the two focuses, and the heading alludes to the course of relocation from A to B. Numerous mathematical procedure on genuine numbers like expansion, deduction, augmentation, and refutation have close analogs for vectors, tasks which submit to the recognizable arithmetical laws of commutativity, associativity, and distributivity. These tasks and related regulations qualify Euclidean vectors to act as an illustration of the more summed up idea of vectors characterized basically as components of a vector space.
Vectors assume a significant part in physical science: the speed and speed increase of a moving article and the powers following up on it can be generally depicted with vectors. Numerous other actual amounts can be conveniently considered vectors. Albeit the majority of them don’t address distances (with the exception of, for instance, position or relocation), their size and heading can in any case be addressed by the length and course of a bolt. The numerical portrayal of an actual vector relies upon the direction framework used to depict it. Other vector-like items that depict actual amounts and change likewise under changes of the direction framework incorporate pseudovectors and tensors.
Vector addition system
A vector expansion framework (VAS) is one of a few numerical demonstrating dialects for the portrayal of dispersed frameworks. Vector expansion frameworks were presented by Richard M. Karp and Raymond E. Mill operator in 1969, and summed up to vector expansion frameworks with states (VASS) by John E. Hopcroft and Jean-Jacques Pansiot in 1979. The two VAS and VASS are comparable in numerous ways to Petri nets presented before via Carl Adam Petri.
Reachability in vector expansion frameworks is Ackermann-finished (and subsequently nonelementary).
Vector space
In science and physical science, a vector space (likewise called a direct space) is a set whose components, frequently called vectors, might be added together and duplicated (“scaled”) by numbers called scalars. Scalars are many times genuine numbers, however can be mind boggling numbers or, all the more by and large, components of any field. The tasks of vector expansion and scalar augmentation should fulfill specific necessities, called vector aphorisms. The terms genuine vector space and complex vector space are frequently used to determine the idea of the scalars: genuine direction space or complex direction space.
Vector spaces sum up Euclidean vectors, which permit displaying of actual amounts, like powers and speed, that poor person just a greatness, yet additionally a bearing. The idea of vector spaces is basic for direct polynomial math, along with the idea of framework, which permits processing in vector spaces. This gives a brief and manufactured way for controlling and concentrating on frameworks of straight conditions.
Vector spaces are described by their aspect, which, generally talking, determines the quantity of free bearings in the space. This intends that, for two vector spaces with similar aspect, the properties that rely just upon the vector-space structure are the very same (actually the vector spaces are isomorphic). A vector space is limited layered in the event that its aspect is a characteristic number. In any case, it is limitless layered, and its aspect is a boundless cardinal. Limited layered vector spaces happen normally in math and related regions. Boundless layered vector spaces happen in numerous areas of math. For instance, polynomial rings are countably boundless layered vector spaces, and many capability spaces have the cardinality of the continuum as an aspect.
Numerous vector spaces that are viewed as in arithmetic are likewise blessed with different designs. This is the situation of algebras, which incorporate field augmentations, polynomial rings, affiliated algebras and Falsehood algebras. This is likewise the situation of topological vector spaces, which incorporate capability spaces, inward item spaces, normed spaces, Hilbert spaces and Banach spaces.
Vector algebra
In math, vector polynomial math might mean:
Straight polynomial math, explicitly the fundamental arithmetical activities of vector expansion and scalar increase; see vector space.
The mathematical tasks in vector analytics, in particular the particular extra design of vectors in 3-layered Euclidean space {R} ^{3} of spot item and particularly cross item. In this sense, vector variable based math is appeared differently in relation to mathematical variable based math, which gives an elective speculation to higher aspects.
A variable based math over a field, a vector space outfitted with a bilinear item
Unique vector algebras of the nineteenth century like quaternions, tessarines, or coquaternions, every one of which has its own item. The vector algebras biquaternions and exaggerated quaternions empowered the upset in physical science called exceptional relativity by giving numerical models.
Case Study on Addition of vectors
Sure, here’s a case study on the addition of vectors:
Suppose you are working on a physics problem that involves the motion of an object in two dimensions. The object is initially at position (2, 5) meters and moves 3 meters to the right and 4 meters upward. You want to find the new position of the object after this motion.
To solve this problem, you need to use vector addition. First, you can represent the initial position of the object as a vector:
A = (2, 5)
Then, you can represent the motion of the object as another vector:
B = (3, 4)
To find the new position of the object, you need to add these two vectors using the rules of vector addition. Specifically, you add their x-components and their y-components separately:
A + B = (2, 5) + (3, 4) = (2 + 3, 5 + 4) = (5, 9)
Therefore, the new position of the object is (5, 9) meters. You can also represent this result as a vector:
C = (5, 9)
This vector represents the displacement of the object from its initial position. Its magnitude can be calculated using the Pythagorean theorem:
|C| = sqrt(5^2 + 9^2) = 10.3 meters
Its direction can be calculated using trigonometry:
theta = arctan(9/5) = 60.3 degrees
Therefore, the object has moved 10.3 meters at an angle of 60.3 degrees from its initial position.
This case study shows how vector addition can be used to solve problems involving the motion of objects in two dimensions. By representing position and motion as vectors, you can use the rules of vector addition to find the resulting displacement of the object.
White paper on Addition of vectors
Here’s a white paper on the addition of vectors:
Introduction: Vectors are an essential concept in mathematics and physics, particularly in the study of motion and forces. Vector addition is a fundamental operation that allows us to combine vectors and determine their resulting direction and magnitude. This white paper provides an overview of vector addition, its properties, and its applications.
Properties of vector addition: The addition of vectors follows several properties that make it a useful tool in solving problems involving vectors. One of the main properties is the commutative property, which states that the order of adding vectors does not affect the result. That is, A + B = B + A. Another important property is the associative property, which states that the grouping of vectors being added does not affect the result. That is, (A + B) + C = A + (B + C). Finally, the distributive property states that the multiplication of a scalar by a vector can be distributed over vector addition. That is, a(A + B) = aA + aB, where “a” is a scalar.
Geometric interpretation of vector addition: Vectors can be represented as directed line segments in a two-dimensional or three-dimensional space. The geometric interpretation of vector addition is the process of placing one vector’s tail at the head of another vector and drawing a line from the tail of the first vector to the head of the second vector. The resulting vector is the vector that connects the tail of the first vector to the head of the second vector. The magnitude and direction of the resulting vector can be calculated using trigonometry.
Applications of vector addition: Vector addition has numerous applications in physics, engineering, and other fields. One of the primary applications is in the study of motion, where vectors are used to represent position, velocity, and acceleration. By adding and subtracting these vectors, we can determine the object’s resulting position and motion. Another application is in the study of forces, where vectors are used to represent the direction and magnitude of forces acting on an object. By adding and subtracting these vectors, we can determine the net force acting on the object.
Conclusion: Vector addition is a powerful tool that allows us to combine vectors and determine their resulting direction and magnitude. Its properties and geometric interpretation make it a useful tool in solving problems involving vectors. Vector addition has numerous applications in physics, engineering, and other fields and is an essential concept for anyone studying these subjects.