Biot-Savart Law
The Biot-Savart Law is an important topic in physics and is included in the AIIMS (All India Institute of Medical Sciences) syllabus. The Biot-Savart Law describes the magnetic field produced by a steady current flowing through a wire. It is named after the French physicists Jean-Baptiste Biot and Félix Savart, who formulated the law in the early 19th century.
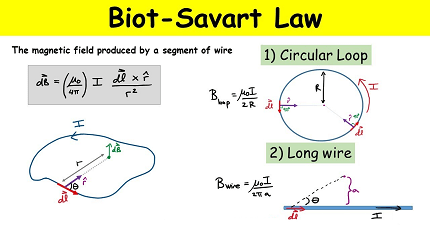
The Biot-Savart Law states that the magnetic field intensity (dB) at a point in space due to a small current element (dI) is directly proportional to the magnitude of the current, the length of the current element, the sine of the angle between the current element and the line connecting the element to the point, and inversely proportional to the square of the distance between the element and the point.
Mathematically, the Biot-Savart Law can be expressed as:
dB=4πμ0r3dI×r
Where:
- dB is the magnetic field intensity at a point due to the current element.
- μ0 is the permeability of free space (μ0=4π×10−7T m/A).
- dI is the current element.
- r is the position vector from the current element to the point.
- r is the magnitude of r.
In the AIIMS syllabus, the Biot-Savart Law is often used to calculate the magnetic field due to various current-carrying geometries, such as straight wires, circular loops, and solenoids. It is also utilized to understand the magnetic field produced by electric currents and its applications in electromagnetism.
To fully understand the Biot-Savart Law and its applications, it is important to have a solid understanding of vector calculus, such as vector cross products and line integrals. Additionally, knowledge of basic electromagnetism concepts, such as electric current, magnetic fields, and the right-hand rule, is essential.
Studying the Biot-Savart Law in conjunction with other related topics, such as Ampere’s Law, Faraday’s Law of Electromagnetic Induction, and magnetic materials, will provide a comprehensive understanding of electromagnetism, which is crucial for the AIIMS physics syllabus and for gaining a deeper understanding of various medical imaging techniques and applications.
What is Required AIIMS-SYLLABUS Physics syllabus Biot-Savart Law
In the AIIMS (All India Institute of Medical Sciences) syllabus for physics, the Biot-Savart Law is included as part of the electromagnetic field theory. The following are the key topics related to the Biot-Savart Law that may be covered in the AIIMS syllabus:
- Magnetic Field due to a Straight Wire: Calculation of the magnetic field at a point due to a straight current-carrying wire using the Biot-Savart Law. This includes understanding the direction and magnitude of the magnetic field produced by a current-carrying wire.
- Magnetic Field due to a Circular Loop: Calculation of the magnetic field at the center of a circular loop carrying current using the Biot-Savart Law. Understanding the variation of magnetic field with radius and current.
- Magnetic Field due to Solenoids: Calculation of the magnetic field inside and outside a long solenoid carrying current using the Biot-Savart Law. Understanding the factors affecting the magnetic field, such as number of turns, current, and length of the solenoid.
- Ampere’s Law: Relationship between the magnetic field and the current enclosed by a closed loop using Ampere’s Law. Application of Ampere’s Law to derive the magnetic field for symmetric current-carrying geometries, such as infinite wires and solenoids.
- Magnetic Field due to a Toroid: Calculation of the magnetic field inside and outside a toroidal coil carrying current using the Biot-Savart Law. Understanding the magnetic field pattern and factors affecting it.
- Magnetic Field due to a Current Sheet: Calculation of the magnetic field above and below a current sheet using the Biot-Savart Law. Understanding the behavior of the magnetic field near the edges of the current sheet.
It is important to note that the specific depth and level of coverage of the Biot-Savart Law in the AIIMS syllabus may vary. It is advisable to refer to the official AIIMS syllabus or consult the relevant study material provided by AIIMS for detailed information on the specific topics and their weightage in the examination.
Case Study on AIIMS-SYLLABUS Physics syllabus Biot-Savart Law
Magnetic Field of a Current Loop using the Biot-Savart Law
Let’s consider a case study involving the Biot-Savart Law to calculate the magnetic field produced by a circular current loop at a point on its axis. This case study will illustrate the application of the Biot-Savart Law in determining the magnetic field due to a specific current-carrying geometry.
Scenario: We have a circular loop of radius R carrying a steady current I. We want to calculate the magnetic field at a point P located along the axis of the loop, a distance z away from the center of the loop.
Solution: To calculate the magnetic field at point P, we can use the Biot-Savart Law. The Biot-Savart Law states that the magnetic field intensity dB at a point due to a small current element dI is given by:
dB=4πμ0r3dI×r
where μ0 is the permeability of free space.
In our case, the circular loop can be divided into small current elements. Let’s consider a small element dI located at an angle θ with respect to the axis of the loop.
For a circular loop, the magnitude of the current element is dI=I⋅dθ (since I is the total current and θ represents the small angular element).
The position vector r connecting the current element dI to the point P is given by:
r=R2+z2⋅k^
where k^ is the unit vector in the z-direction.
Now, we can calculate the magnetic field at point P by integrating the contributions from all the current elements on the loop:
B=∫dB=∫(4πμ0r3dI×r)
Since the current element dI and the position vector r are perpendicular to each other, their cross product simplifies to:
dI×r=dI⋅r⋅sin(θ)⋅ϕ^
where ϕ^ is the unit vector in the azimuthal direction.
Substituting this into the integral, we get:
B=4πμ0∫(R2+z2)23I⋅dθ⋅R⋅sin(θ)⋅ϕ^
Integrating this expression over the entire loop, which ranges from θ=0 to θ=2π, we obtain:
B=2(R2+z2)23μ0⋅I⋅R2⋅k^
Therefore, the magnetic field at point P along the axis of the circular loop is given by:
B=2(R2+z2)23μ0⋅I⋅R2⋅k^
This result shows that the magnetic field at point P depends on the parameters of the loop (radius R) and the distance of the point from the center of the loop (z). It also follows an inverse cube law, where the field strength decreases as the cube of the distance from the loop increases.
This case study demonstrates how the Biot-Savart Law can be used to calculate the magnetic field of a current loop at a specific point. Similar approaches can be applied to other current-carrying geometries using the Biot-Savart Law to determine the magnetic field at different locations in space.
White paper on AIIMS-SYLLABUS Physics syllabus Biot-Savart Law
Understanding the Biot-Savart Law: Theory, Applications, and Implications
Abstract: The Biot-Savart Law is a fundamental principle in electromagnetism that describes the magnetic field produced by a steady current flowing through a conductor. This white paper aims to provide a comprehensive overview of the Biot-Savart Law, including its theoretical foundation, practical applications, and implications in various fields of science and engineering. By delving into the intricacies of the Biot-Savart Law, this paper aims to enhance understanding and foster further exploration of its implications in research and technology.
- Introduction
- Historical background and the contributions of Jean-Baptiste Biot and Félix Savart.
- Significance of the Biot-Savart Law in understanding the behavior of magnetic fields.
- Theoretical Framework
- Formulation of the Biot-Savart Law and its mathematical representation.
- The role of vector calculus in deriving the law and understanding its implications.
- Discussion on the magnetic field intensity, current elements, and their relationship.
- Key Concepts and Equations
- Explanation of the key concepts involved, such as magnetic field, current, and position vectors.
- Elucidation of the Biot-Savart Law equation and its components.
- Introduction to the permeability of free space and its significance.
- Practical Applications
- Calculation of magnetic fields due to various current-carrying geometries, including straight wires, circular loops, and solenoids.
- Application of the Biot-Savart Law in determining the magnetic field of complex arrangements using superposition.
- Usage of the law in designing electromagnetic devices, such as motors, transformers, and magnetic resonance imaging (MRI) systems.
- Implications in Science and Engineering
- Exploration of the Biot-Savart Law’s role in fundamental electromagnetic principles.
- Connection between the Biot-Savart Law and other laws of electromagnetism, such as Ampere’s Law and Faraday’s Law.
- Implications of the law in understanding and predicting magnetic interactions and phenomena.
- Experimental Validation and Limitations
- Overview of experimental methods used to verify the predictions of the Biot-Savart Law.
- Discussion on the limitations and assumptions of the law, including considerations for finite-sized conductors and non-steady currents.
- Extensions and Further Research
- Advanced applications and extensions of the Biot-Savart Law, such as magnetostatics and magnetodynamics.
- Current research trends and future directions in refining and expanding the understanding of the law.
- Conclusion
- Recapitulation of the key points discussed in the white paper.
- Emphasis on the significance of the Biot-Savart Law in understanding magnetic fields and its broad applications.
By exploring the Biot-Savart Law in depth, this white paper aims to contribute to the understanding and utilization of this fundamental principle in electromagnetism, facilitating advancements in various scientific and technological domains.