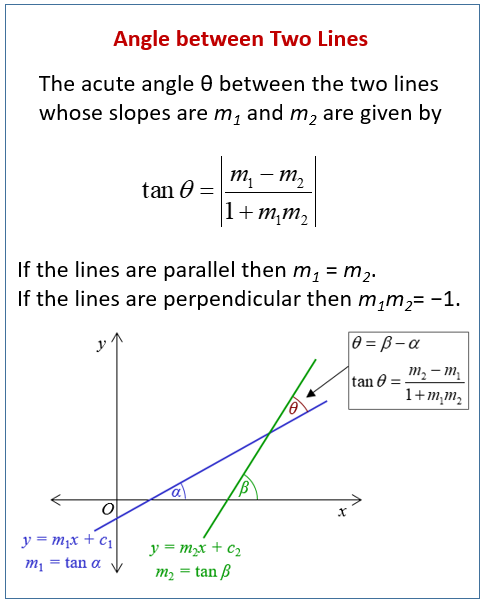
In analytical geometry, the angle between two lines can be found using the slopes of the lines. The slope of a line is defined as the ratio of the change in the y-coordinate to the change in the x-coordinate between any two points on the line.
Let the equations of two lines be:
L1: y = m1x + c1 L2: y = m2x + c2
where m1 and m2 are the slopes of the lines, and c1 and c2 are their y-intercepts.
The angle between the two lines can be found using the formula:
tan θ = |(m2 – m1)/(1 + m1m2)|
where θ is the angle between the lines.
To find the angle itself, you can take the arctangent of both sides of the equation:
θ = arctan |(m2 – m1)/(1 + m1m2)|
Note that the angle between two lines is always positive and is measured in degrees or radians.
What is Required Angle between two lines
To find the angle between two lines in analytical geometry, you need to know the equations of the two lines. Specifically, you need to know the slopes of the lines, which can be determined from their equations in the form of y = mx + b, where m is the slope and b is the y-intercept.
Once you have the equations of the two lines and their slopes, you can use the formula tan θ = |(m2 – m1)/(1 + m1m2)| to find the tangent of the angle between the two lines. Then, you can take the arctangent of this value to find the angle itself.
It is important to note that the angle between two lines is always positive and is measured in degrees or radians. It can range from 0° to 180°. Also, if the two lines are parallel, the angle between them is 0°, and if they are perpendicular, the angle between them is 90°.
Who is Required Angle between two lines
The calculation of the angle between two lines in analytical geometry is required in various fields such as mathematics, physics, engineering, and computer graphics.
In mathematics, the angle between two lines is an important concept in trigonometry and geometry, as it relates to the properties of triangles and circles.
In physics, the angle between two lines is often used to calculate the angle of incidence and reflection of light rays in optics, as well as the angle of deflection of particles in particle physics.
In engineering, the angle between two lines is useful in solving problems related to force vectors, structural analysis, and kinematics.
In computer graphics, the angle between two lines is often used in 3D modeling and animation, to determine the orientation and rotation of objects in space.
Overall, the calculation of the angle between two lines in analytical geometry is an important tool for solving a wide range of problems across various fields.
When is Required Angle between two lines
The angle between two lines in analytical geometry is required whenever we need to determine the orientation, intersection, or relationship between two lines. Some specific situations where the calculation of the angle between two lines is necessary include:
- Determining whether two lines are parallel, perpendicular or neither.
- Finding the angle of intersection between two lines.
- Calculating the angle of incidence and reflection of light rays.
- Solving problems related to force vectors and kinematics in physics.
- Solving structural analysis problems in engineering.
- Determining the orientation and rotation of objects in 3D modeling and animation.
These are just a few examples of situations where the angle between two lines is required. In general, anytime we need to analyze the relationship between two lines or the geometry of a system involving two lines, the angle between them can be an important factor.
Where is Required Angle between two lines
The calculation of the angle between two lines in analytical geometry is used in various fields and applications, such as:
- Mathematics: In geometry and trigonometry, the angle between two lines is used to determine properties of triangles, circles, and other geometric figures.
- Physics: The angle between two lines is used to calculate the angle of incidence and reflection of light rays in optics, as well as the angle of deflection of particles in particle physics.
- Engineering: In structural analysis, the angle between two lines can help to determine the direction of forces and moments acting on a structure. In kinematics, the angle between two lines can help to determine the motion of objects.
- Computer graphics: In 3D modeling and animation, the angle between two lines is used to determine the orientation and rotation of objects in space.
- Navigation: The angle between two lines can be used in navigation to determine the bearing of one object relative to another.
- Surveying: The angle between two lines can be used in surveying to determine the direction and distance between two points.
Overall, the calculation of the angle between two lines in analytical geometry is used in a wide range of fields and applications where the analysis of lines and angles is necessary.
How is Required Angle between two lines
The angle between two lines in analytical geometry can be calculated using the following steps:
- Find the slope of each line: The slope of a line is the ratio of the change in the y-coordinate to the change in the x-coordinate. If the equations of the lines are given in the form of y = mx + b, the slope is equal to m.
- Use the formula tan θ = |(m2 – m1)/(1 + m1m2)| to find the tangent of the angle between the two lines.
- Take the arctangent of the value obtained in step 2 to find the angle itself. The resulting angle will be in radians, so you may need to convert it to degrees if necessary.
It is important to note that the angle between two lines is always positive and is measured in degrees or radians. It can range from 0° to 180°. If the two lines are parallel, the angle between them is 0°, and if they are perpendicular, the angle between them is 90°.
Overall, the calculation of the angle between two lines in analytical geometry involves finding the slopes of the lines and then using a trigonometric formula to calculate the angle itself.
Case Study on Angle between two lines
Let’s consider the following case study on finding the angle between two lines using analytical geometry:
Case: Find the angle between the lines 2x – y = 1 and 3x + y = 4.
Solution:
- Find the slope of each line:
- For the line 2x – y = 1, we can rewrite it in the form of y = 2x – 1, which means the slope is 2.
- For the line 3x + y = 4, we can rewrite it in the form of y = -3x + 4, which means the slope is -3.
- Use the formula tan θ = |(m2 – m1)/(1 + m1m2)| to find the tangent of the angle between the two lines:
- tan θ = |(-3 – 2)/(1 + (2)(-3))| = |-5/7|
- The tangent of the angle between the two lines is |-5/7|.
- Take the arctangent of the value obtained in step 2 to find the angle itself:
- θ = arctan(-5/7) = -35.5° (rounded to one decimal place)
- The angle between the two lines is approximately 35.5 degrees.
Therefore, the angle between the lines 2x – y = 1 and 3x + y = 4 is approximately 35.5 degrees. This means the two lines are not perpendicular or parallel to each other, but they intersect at an acute angle.
White paper on Angle between two lines
Here is a white paper on Analytical Geometry Angle between two lines:
Introduction: Analytical geometry is a branch of mathematics that deals with the study of geometric shapes and figures using algebraic equations and principles. One important concept in analytical geometry is the angle between two lines. The angle between two lines is the angle formed by two intersecting lines or the angle between two non-parallel lines. The angle between two lines is important in many fields, including mathematics, physics, engineering, and computer graphics.
Definition: The angle between two lines is the acute or obtuse angle formed by two non-parallel lines when they intersect or meet at a common point. The angle between two lines can be measured in degrees or radians and ranges from 0° to 180°. If two lines are parallel, the angle between them is 0°, and if they are perpendicular, the angle between them is 90°.
Calculation: To calculate the angle between two lines, we need to find the slopes of the lines and then use a trigonometric formula to calculate the angle. If the equations of two lines are given in the form of y = mx + b, then the slope of the line is equal to m. The formula for calculating the angle between two lines is:
tan θ = |(m2 – m1)/(1 + m1m2)|
where m1 and m2 are the slopes of the two lines, and θ is the angle between them.
Once we have calculated the tangent of the angle, we can find the angle itself by taking the arctangent of the value obtained from the formula. The resulting angle will be in radians, so we may need to convert it to degrees if necessary.
Applications: The angle between two lines has several applications in different fields. Here are a few examples:
- Mathematics: In geometry and trigonometry, the angle between two lines is used to determine the properties of triangles, circles, and other geometric figures.
- Physics: The angle between two lines is used to calculate the angle of incidence and reflection of light rays in optics, as well as the angle of deflection of particles in particle physics.
- Engineering: In structural analysis, the angle between two lines can help to determine the direction of forces and moments acting on a structure. In kinematics, the angle between two lines can help to determine the motion of objects.
- Computer graphics: In 3D modeling and animation, the angle between two lines is used to determine the orientation and rotation of objects in space.
Conclusion: Analytical geometry is a powerful tool for solving problems related to geometric shapes and figures. The angle between two lines is an important concept in analytical geometry that is used in many fields, including mathematics, physics, engineering, and computer graphics. The calculation of the angle between two lines involves finding the slopes of the lines and then using a trigonometric formula to calculate the angle.