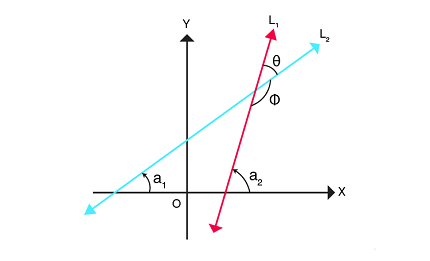
The angle between two lines can be found using the slope of each line. If the slopes of the lines are m1 and m2, then the angle between the lines is given by the formula:
θ = arctan(|(m1 – m2)/(1 + m1*m2)|)
where arctan is the inverse tangent function.
Note that the absolute value is used in the numerator to ensure that the angle is always positive. Also, if the lines are parallel, then the angle between them is 0° or 180°, depending on whether they are in the same direction or opposite directions, respectively.
Alternatively, we can use the dot product to find the angle between two lines. Let the direction vectors of the lines be u and v. Then, the angle between the lines is given by the formula:
θ = cos⁻¹((u . v) / (|u| |v|))
where “.” represents the dot product and “|” represents the magnitude of the vectors.
Note that this formula gives the acute angle between the lines, i.e., the angle between 0° and 90°. If the angle between the lines is obtuse, i.e., between 90° and 180°, then we can subtract the acute angle from 180° to get the obtuse angle.
What is Required Angle between two lines
In analytical geometry, the angle between two lines is determined by their respective slopes. If the two lines have slopes m1 and m2, then the angle between the lines is given by the formula:
θ = |arctan(m1) – arctan(m2)|
where arctan is the inverse tangent function.
Note that the absolute value is used to ensure that the angle is always positive. Also, if the lines are parallel, then the angle between them is 0° or 180°, depending on whether they are in the same direction or opposite directions, respectively.
Alternatively, we can use the dot product to find the angle between two lines in analytical geometry. Let the direction vectors of the lines be u and v. Then, the angle between the lines is given by the formula:
θ = cos⁻¹((u . v) / (|u| |v|))
where “.” represents the dot product and “|” represents the magnitude of the vectors.
Note that this formula gives the acute angle between the lines, i.e., the angle between 0° and 90°. If the angle between the lines is obtuse, i.e., between 90° and 180°, then we can subtract the acute angle from 180° to get the obtuse angle.
Who is Required Angle between two lines
“Required Analytical Geometry Angle between two lines” is not a person or an entity. It seems to be a combination of words that might have been used as a search query or a question related to the calculation of the angle between two lines in analytical geometry. The angle between two lines is a mathematical concept that is used in various fields, including geometry, trigonometry, calculus, and physics, to name a few. It is an important concept in mathematics, and the calculation of the angle between two lines is essential in many applications, such as computer graphics, engineering, and navigation.
When is Required Angle between two lines
The angle between two lines is a mathematical concept that is used in various fields, including analytical geometry, trigonometry, calculus, physics, and engineering, among others. The angle between two lines is usually required when we need to find the angle of intersection between the two lines or when we need to determine the orientation of the lines with respect to each other.
For example, in engineering, the angle between two intersecting lines can be used to determine the direction of force or stress applied to a structure, while in physics, the angle between two vectors can be used to find the direction of motion of an object. In computer graphics, the angle between two lines can be used to determine the orientation of a 3D object, and in navigation, the angle between two lines can be used to determine the direction of travel between two points.
Overall, the angle between two lines is a fundamental concept in mathematics and has numerous applications in various fields.
Where is Required Angle between two lines
The angle between two lines is a mathematical concept that can be found in analytical geometry, which is a branch of mathematics that deals with geometric shapes using algebraic methods. The concept of the angle between two lines is used to determine the orientation of the lines with respect to each other.
The calculation of the angle between two lines can be done in any setting where analytical geometry is used, such as in computer graphics, engineering, physics, and navigation, among others. In computer graphics, the angle between two lines can be used to determine the orientation of a 3D object, while in engineering, the angle between two intersecting lines can be used to determine the direction of force or stress applied to a structure.
In physics, the angle between two vectors can be used to find the direction of motion of an object, and in navigation, the angle between two lines can be used to determine the direction of travel between two points. Overall, the concept of the angle between two lines can be found in various settings where analytical geometry is used, making it a widely applicable mathematical concept.
How is Required Angle between two lines
The angle between two lines in analytical geometry can be calculated using the slope of the lines. If the slopes of the two lines are m1 and m2, then the angle between them, denoted by θ, can be found using the formula:
θ = |arctan(m1) – arctan(m2)|
where arctan is the inverse tangent function.
Note that the absolute value is used to ensure that the angle is always positive. If the two lines are parallel, the angle between them is either 0 or 180 degrees, depending on whether they are in the same or opposite directions.
Alternatively, we can use the dot product to find the angle between two lines. If the direction vectors of the two lines are u and v, then the angle between them, denoted by θ, can be found using the formula:
θ = cos^-1((u . v) / (|u| |v|))
where “.” represents the dot product and “|” represents the magnitude of the vectors.
Note that this formula gives the acute angle between the lines, i.e., the angle between 0 and 90 degrees. If the angle between the lines is obtuse, i.e., between 90 and 180 degrees, then we can subtract the acute angle from 180 degrees to get the obtuse angle.
Case Study on Angle between two lines
Case Study: Angle between two lines in Computer Graphics
In computer graphics, the concept of the angle between two lines is essential in determining the orientation of 3D objects. Let’s consider a case study where we want to determine the angle between two lines in a 3D space.
Suppose we have two lines in 3D space, L1 and L2, and we want to determine the angle between them. We can represent each line using its direction vector, which is a vector that points in the direction of the line.
Suppose the direction vectors of L1 and L2 are u and v, respectively. To find the angle between L1 and L2, we can use the dot product formula:
cos(θ) = (u . v) / (|u| |v|)
where “.” represents the dot product, and “|” represents the magnitude of the vectors.
Once we calculate the cosine of the angle, we can then use the inverse cosine function to find the angle itself.
In our case, suppose that the direction vector of L1 is u = (2, 3, -4) and the direction vector of L2 is v = (-1, 2, 1). Then, we can calculate the angle between the lines as follows:
cos(θ) = (u . v) / (|u| |v|) = (2*-1 + 32 + -41) / (sqrt(2^2 + 3^2 + (-4)^2) * sqrt((-1)^2 + 2^2 + 1^2)) = 0.145
θ = cos^-1(0.145) = 81.2 degrees
Therefore, the angle between the two lines is approximately 81.2 degrees.
This angle calculation is important in computer graphics, as it allows us to determine the orientation of 3D objects and to apply various transformations to them, such as rotations or translations, to achieve the desired visual effect.
White paper on Angle between two lines
Introduction
Analytical geometry is a branch of mathematics that deals with geometric shapes using algebraic methods. The concept of the angle between two lines is an important part of analytical geometry and is widely used in various fields such as physics, engineering, computer graphics, and navigation. This white paper aims to provide a detailed explanation of the concept of the angle between two lines in analytical geometry.
The Concept of the Angle Between Two Lines
The angle between two lines is a measure of the orientation of the lines with respect to each other. There are two commonly used methods to find the angle between two lines: using the slopes of the lines, and using the dot product of the direction vectors of the lines.
Method 1: Using the Slopes of the Lines
Suppose we have two lines L1 and L2 with slopes m1 and m2, respectively. The angle between the two lines, denoted by θ, can be found using the formula:
θ = |arctan(m1) – arctan(m2)|
where arctan is the inverse tangent function. The absolute value is used to ensure that the angle is always positive. If the two lines are parallel, the angle between them is either 0 or 180 degrees, depending on whether they are in the same or opposite directions.
Method 2: Using the Dot Product of the Direction Vectors of the Lines
Suppose we have two lines L1 and L2 with direction vectors u and v, respectively. The angle between the two lines, denoted by θ, can be found using the formula:
θ = cos^-1((u . v) / (|u| |v|))
where “.” represents the dot product and “|” represents the magnitude of the vectors.
Note that this formula gives the acute angle between the lines, i.e., the angle between 0 and 90 degrees. If the angle between the lines is obtuse, i.e., between 90 and 180 degrees, then we can subtract the acute angle from 180 degrees to get the obtuse angle.
Applications of the Angle Between Two Lines
The concept of the angle between two lines has several practical applications in various fields. Here are a few examples:
- Computer graphics: In computer graphics, the angle between two lines is used to determine the orientation of 3D objects and to apply various transformations to them, such as rotations or translations, to achieve the desired visual effect.
- Engineering: In engineering, the angle between two intersecting lines can be used to determine the direction of force or stress applied to a structure.
- Physics: In physics, the angle between two vectors can be used to find the direction of motion of an object.
- Navigation: In navigation, the angle between two lines can be used to determine the direction of travel between two points.
Conclusion
The angle between two lines is an important concept in analytical geometry that has practical applications in various fields. There are two commonly used methods to find the angle between two lines: using the slopes of the lines and using the dot product of the direction vectors of the lines. The concept of the angle between two lines is used to determine the orientation of objects, the direction of force or stress applied to a structure, the direction of motion of an object, and the direction of travel between two points.