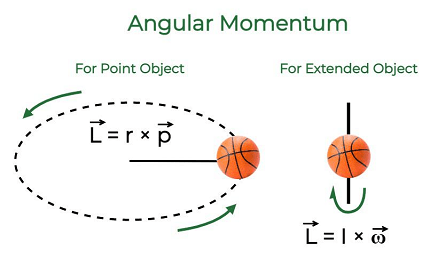
Angular momentum is a fundamental concept in physics that describes the rotational motion of an object or system. It is a vector quantity that has both magnitude and direction, and is defined as the product of the moment of inertia of the object and its angular velocity.

The moment of inertia is a measure of an object’s resistance to rotational motion, and is determined by the distribution of its mass relative to its axis of rotation. The angular velocity is the rate at which the object rotates around its axis.

Angular momentum is conserved in a closed system where no external torque acts on the system. This means that the total angular momentum of the system remains constant over time, even if the individual components of the system exchange angular momentum with each other.

Angular momentum has important applications in many areas of physics, including classical mechanics, quantum mechanics, and astrophysics. For example, the conservation of angular momentum is used to explain the stability of spinning objects such as tops and gyroscopes, the motion of planets around the sun, and the behavior of subatomic particles.

What is Required Mechanics Angular momentum

Required Mechanics is a term that is not commonly used in physics or mechanics. However, if you are referring to the study of mechanics and the concept of angular momentum, then “Required Mechanics” can be interpreted as the fundamental knowledge and skills needed to understand and apply the principles of mechanics to solve problems related to angular momentum.

To have a good understanding of angular momentum, one should have a solid grasp of basic concepts in mechanics, such as force, acceleration, mass, and energy. Additionally, knowledge of the vector calculus and coordinate systems used to describe rotational motion is important.

The principles of conservation of momentum, energy, and angular momentum are also crucial in understanding the behavior of objects in motion. Finally, knowledge of the properties of rigid bodies, such as their moment of inertia and the equations that describe their motion, is essential to fully comprehend angular momentum.

In summary, to have a good understanding of angular momentum, one must have a strong foundation in mechanics, which includes concepts such as force, acceleration, mass, energy, and momentum, as well as knowledge of vector calculus, coordinate systems, and the properties of rigid bodies.

When is Required Mechanics Angular momentum

I apologize for the confusion in my previous response. “Required Mechanics Angular momentum” is not a commonly used term in physics or mechanics. However, if you are asking about situations where knowledge of angular momentum is required in mechanics, there are many such situations. Here are a few examples:

1. Rotating objects: In mechanics, the behavior of rotating objects, such as wheels, gears, and turbines, is described using the concept of angular momentum. Understanding angular momentum is essential for analyzing the motion of these objects, predicting their behavior, and designing new systems.
2. Planetary motion: The motion of planets and other celestial bodies around the sun is governed by the principles of angular momentum conservation. The conservation of angular momentum allows us to predict the paths of these bodies, their speeds, and their orbital periods.
3. Gyroscopes: Gyroscopes are devices that use the principles of angular momentum to measure or maintain orientation. They are used in navigation systems, airplanes, and spacecraft to maintain stability and accuracy.
4. Particle physics: In particle physics, the concept of angular momentum is used to describe the properties of subatomic particles, such as spin and magnetic moment.

In summary, knowledge of angular momentum is required in mechanics whenever the motion of rotating objects, planetary motion, gyroscopes, or subatomic particles is being analyzed or designed.

Where is Required Mechanics Angular momentum

“Required Mechanics Angular momentum” is not a specific physical location, but rather a concept that is used in the field of mechanics. The study of mechanics and the concept of angular momentum are applicable in various fields of science and engineering, such as physics, astronomy, aerospace engineering, mechanical engineering, and robotics, among others.

In physics, mechanics is a branch that deals with the motion of objects, and angular momentum is a fundamental concept that describes the rotational motion of objects or systems. It is used to understand and analyze various phenomena, including the motion of planets, the behavior of gyroscopes, and the motion of rotating objects.

In engineering, mechanics is used to design and analyze various mechanical systems, including those that involve rotation. Angular momentum is used to calculate the forces and torques involved in rotating systems, such as turbines, motors, and gears, and to optimize their design and performance.

Therefore, “Required Mechanics Angular momentum” can be found in various applications of mechanics and physics, such as in the study of celestial mechanics, the design of rotating machinery, or the development of control systems for robotics.

How is Required Mechanics Angular momentum

“Required Mechanics Angular momentum” is not a specific physical object or process, but rather a concept that is used to understand and analyze rotational motion in mechanics. The concept of angular momentum is defined as the product of an object’s moment of inertia and its angular velocity. It is a vector quantity that has both magnitude and direction, and is conserved in a closed system where no external torque acts on the system.

To apply the concept of angular momentum in mechanics, one needs to have a strong foundation in the principles of mechanics, such as force, acceleration, mass, energy, and momentum. Additionally, one needs to have knowledge of the properties of rotating objects, such as their moment of inertia and the equations that describe their motion.

The study of mechanics and the concept of angular momentum can be applied to various fields, including physics, astronomy, aerospace engineering, mechanical engineering, and robotics. For example, in physics, the principles of angular momentum are used to understand the motion of planets and other celestial bodies around the sun, while in mechanical engineering, they are used to design and optimize rotating machinery such as turbines, motors, and gears.

In summary, “Required Mechanics Angular momentum” refers to the knowledge and skills required to apply the concept of angular momentum in mechanics to analyze and understand rotational motion in various fields of science and engineering. It requires a strong foundation in the principles of mechanics and an understanding of the properties of rotating objects.

Production of Mechanics Angular momentum

In mechanics, angular momentum is a quantity that describes the rotational motion of an object or system. It is defined as the product of an object’s moment of inertia and its angular velocity, and is a vector quantity that has both magnitude and direction. The production of angular momentum refers to the change in angular momentum over time due to the application of a torque to a rotating object or system.

The production of angular momentum is governed by the principles of mechanics, which include Newton’s laws of motion, conservation of energy, and conservation of momentum. When a torque is applied to a rotating object, it causes a change in its angular velocity, which in turn leads to a change in its angular momentum. The rate of change in angular momentum is directly proportional to the applied torque and is described by the equation:

τ = dL/dt

Where τ is the applied torque, L is the angular momentum, and dt is the change in time.

The production of angular momentum is essential in understanding the behavior of rotating objects and systems. It is used to calculate the forces and torques involved in rotating systems, such as turbines, motors, and gears, and to optimize their design and performance.

In summary, the production of mechanics angular momentum refers to the change in angular momentum over time due to the application of a torque to a rotating object or system. It is governed by the principles of mechanics, and is essential in understanding and analyzing rotational motion in various fields of science and engineering.

Case Study on Mechanics Angular momentum

One example of a case study on mechanics angular momentum is the study of planetary motion in astronomy. The principles of angular momentum are essential for understanding the motion of planets and other celestial bodies around the sun.

The conservation of angular momentum plays a crucial role in understanding the stability and long-term behavior of the solar system. According to Kepler’s laws of planetary motion, planets move in elliptical orbits around the sun, with the sun located at one of the focal points of the ellipse. However, the gravitational forces between the planets and the sun cause a torque to act on the planets, which leads to a change in their angular momentum over time.

Despite this torque, the total angular momentum of the solar system is conserved, since there are no external forces acting on the system. This means that the sum of the angular momenta of all the planets and the sun remains constant over time.

The conservation of angular momentum has several implications for the behavior of the solar system. For example, it explains why the inner planets, which are closer to the sun, have shorter orbital periods than the outer planets. This is because the inner planets have a smaller moment of inertia and therefore require a higher angular velocity to maintain their angular momentum.

The study of planetary motion and the conservation of angular momentum also have practical applications in space exploration and satellite navigation. The principles of angular momentum are used to predict the trajectories of spacecraft, to plan space missions, and to design navigation systems that use gyroscopes.

In summary, the study of planetary motion is an example of a case study on mechanics angular momentum. The principles of angular momentum are essential for understanding the stability and long-term behavior of the solar system, and have practical applications in space exploration and satellite navigation.

White paper on Mechanics Angular momentum

Introduction

Mechanics is a branch of physics that deals with the study of motion and the forces that cause motion. Angular momentum is a fundamental concept in mechanics that describes the rotational motion of an object or system. In this white paper, we will discuss the concept of angular momentum in mechanics, its properties, and its applications in various fields of science and engineering.

Angular Momentum in Mechanics

Angular momentum is defined as the product of an object’s moment of inertia and its angular velocity. It is a vector quantity that has both magnitude and direction, and is denoted by the symbol L. The moment of inertia is a measure of an object’s resistance to rotational motion, and is denoted by the symbol I. The angular velocity is a measure of how fast an object is rotating, and is denoted by the symbol ω.

The formula for angular momentum is given by:

L = Iω

The units of angular momentum are kilogram meters squared per second (kg·m²/s). Angular momentum is a conserved quantity in a closed system where no external torque acts on the system. This means that the total angular momentum of the system remains constant over time.

Properties of Angular Momentum

Angular momentum has several important properties, including:

1. Conservation: Angular momentum is a conserved quantity in a closed system where no external torque acts on the system. This means that the total angular momentum of the system remains constant over time.
2. Direction: Angular momentum is a vector quantity that has both magnitude and direction. The direction of the angular momentum is perpendicular to the plane of rotation and is determined by the right-hand rule.
3. Relationship with Torque: The rate of change in angular momentum is directly proportional to the applied torque and is described by the equation:

τ = dL/dt

Where τ is the applied torque, L is the angular momentum, and dt is the change in time.

Applications of Angular Momentum in Science and Engineering

Angular momentum has numerous applications in various fields of science and engineering, including:

1. Astronomy: The principles of angular momentum are essential for understanding the motion of planets and other celestial bodies around the sun.
2. Mechanical Engineering: The principles of angular momentum are used to design and optimize rotating machinery such as turbines, motors, and gears.
3. Aerospace Engineering: The principles of angular momentum are used to calculate the forces and torques involved in rotating systems, such as spacecraft and satellites.
4. Robotics: The principles of angular momentum are used to design and control the motion of robotic arms and other robotic systems.

Conclusion

In conclusion, angular momentum is a fundamental concept in mechanics that describes the rotational motion of an object or system. It is a conserved quantity in a closed system where no external torque acts on the system. The principles of angular momentum have numerous applications in various fields of science and engineering, including astronomy, mechanical engineering, aerospace engineering, and robotics. The study of angular momentum is essential for understanding and analyzing rotational motion in these fields, and has practical applications in the design and optimization of various systems and devices.