
“Average” is a statistical term that refers to a measure of central tendency, which is the typical or common value in a set of data. There are several types of averages, including the mean, median, and mode.
- The mean, also known as the arithmetic mean, is calculated by adding up all the values in a dataset and dividing by the number of values.
- The median is the middle value in a dataset when the values are arranged in order from smallest to largest.
- The mode is the value that appears most frequently in a dataset.
The choice of which average to use depends on the type of data and the purpose of the analysis. In some cases, multiple averages may be calculated and compared to provide a more complete understanding of the dataset.
Talk:Average

| This article is within the scope of the WikiProject Statistics, a collaborative effort to improve the coverage of statistics on Wikipedia. If you would like to participate, please visit the project page or join the discussion.CThis article has been rated as C-Class on the quality scale. High This article has been rated as High-importance on the importance scale. |

| Mathematics portalThis article is within the scope of WikiProject Mathematics, a collaborative effort to improve the coverage of mathematics on Wikipedia. If you would like to participate, please visit the project page, where you can join the discussion and see a list of open tasks.CThis article has been rated as C-Class on the project’s quality scale. Mid This article has been rated as Mid-priority on the project’s priority scale. |
Average 1
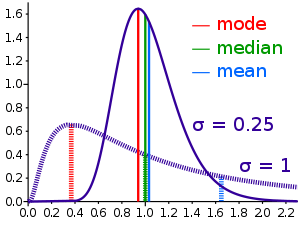
A normal is the “typical” number of a gathering of numbers made by blending the gathering of numbers.
In math, a normal is known as a mean. It very well may be found by adding the numbers, then isolating the response by the quantity of numbers there were. There are different sorts of mean, and different things that are in some cases considered “normal” like middle or mode (measurements).
Moving average
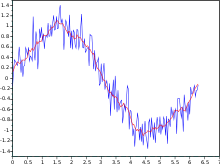
In measurements, a moving normal (moving normal or running normal) is an estimation to break down data of interest by making a progression of midpoints of various choices of the full informational index. It is likewise called a moving mean (MM) or moving mean and is a sort of limited drive reaction channel. Varieties include: straightforward, aggregate, or weighted structures (depicted beneath).
Given a progression of numbers and a decent subset size, the primary component of the moving normal is gotten by taking the normal of the underlying fixed subset of the number series. Then, at that point, the subset is adjusted by “moving forward”; that is, barring the principal number of the series and remembering the following incentive for the subset.
A moving normal is usually utilized with time series information to streamline transient vacillations and feature longer-term patterns or cycles. The limit between present moment and long haul relies upon the application, and the boundaries of the moving typical will be set in like manner. It is likewise utilized in financial aspects to analyze GDP, business or other macroeconomic time series. Numerically, a moving normal is a kind of convolution thus it very well may be seen to act as an illustration of a low-pass channel utilized in signal handling. When utilized with non-time series information, a moving typical channels higher recurrence parts with practically no particular association with time, albeit commonly some sort of requesting is suggested. Seen shortsightedly it very well may be viewed as smoothing the information.
Total average
Complete normal is a baseball measurement formulated by sportswriter Thomas Boswell and presented in the 1978. It was likewise portrayed in his 1982 article “Welcome to the universe of All out Normal where a walk is on par with a hit”. Estimating a hitter’s general hostile commitments, on the premise that “everything bases are made equal is planned”. The measurement was remembered for issues of Inside Sports.
The meaning of the measurement is straightforward. A player gets a credit for each base collected and a punishment for each out made. So a player gets one credit for a solitary, walk, taken base or being hit by a pitch; two for a twofold; three for a triple; and four for a grand slam. A player’s complete normal is determined by adding the collected bases and separating by the quantity of outs the player makes.
Condition of average
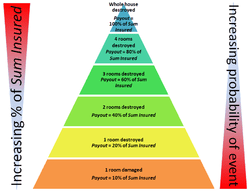
State of normal (likewise called underinsurance in the U.S., or guideline of normal, likely to average, or master rata state of normal in District nations) is the insurance term utilized while working out a payout against a case where the contract underestimates the total safeguarded. In case of fractional misfortune, the sum paid against a case will be in a similar extent as the worth of the underinsurance.
The recipe utilized is

where Payout is the sum paid out by the strategy, Changed Misfortune is the feasible sum from the sum guaranteed against the approach after a misfortune, Aggregate Safeguarded is the greatest sum to be paid out by the strategy, and Current Worth is the worth the strategy ought to be protected for. Underinsurance happens when Aggregate Protected is not exactly Current Worth.
Aggregate Guaranteed is the greatest sum that can be paid out and is just paid out in instances of absolute obliteration. Where fractional obliteration happens (a more normal event than complete annihilation), Payout is master rata in accordance with the underinsurance. This is because of insurance agency putting together the charges with respect to their gamble of losing the full Aggregate Guaranteed against absolute annihilation occasions.
Case Study on Average
A local farmer named John grows different crops on his farm throughout the year, including corn, soybeans, and wheat. He wants to analyze the yield of each crop over the last five years to determine their average production.
John has the following data for each crop’s yield in bushels per acre for the past five years:
- Corn: 160, 170, 180, 165, 175
- Soybeans: 50, 55, 60, 65, 70
- Wheat: 35, 40, 30, 50, 45
John wants to calculate the mean, median, and mode for each crop’s yield over the five-year period to get a better understanding of the production trend for each crop.
To calculate the mean yield, John adds up the yield for each year and divides the sum by the total number of years. The results for each crop are:
- Corn: (160+170+180+165+175)/5 = 170 bushels per acre
- Soybeans: (50+55+60+65+70)/5 = 60 bushels per acre
- Wheat: (35+40+30+50+45)/5 = 40 bushels per acre
Next, John calculates the median yield, which is the middle value when the yield data is arranged in numerical order. If there is an even number of values, the median is the average of the two middle values. The results for each crop are:
- Corn: The median yield is 170 bushels per acre since there are an odd number of values.
- Soybeans: The median yield is 60 bushels per acre since there are an odd number of values.
- Wheat: The median yield is 40 bushels per acre since there are an odd number of values.
Finally, John calculates the mode, which is the value that appears most frequently in the yield data. The results for each crop are:
- Corn: The mode yield is 175 bushels per acre since it appears twice.
- Soybeans: There is no mode since all yield values appear once.
- Wheat: The mode yield is 35 bushels per acre since it appears once and is the lowest value.
Based on these calculations, John can see that the average yield for corn was the highest, followed by soybeans and then wheat. He can use this information to make informed decisions about which crops to plant in future seasons and how to allocate his resources.
White paper on Average
Understanding Averages: The Basics
Introduction
The concept of averages is used in a variety of fields, from statistics and mathematics to finance and business. At its core, an average is a statistical measure that represents the typical value of a set of data. There are different types of averages that can be used depending on the data set and the purpose of the analysis. In this paper, we will explore the basics of averages, including their definition, types, and uses.
Definition
An average is a value that represents the central tendency of a set of data. It is calculated by summing up all the data points and dividing by the total number of data points. For example, if we have a set of data that includes the numbers 5, 10, 15, 20, and 25, the average can be calculated by adding these numbers and dividing by 5 (the total number of data points):
(5 + 10 + 15 + 20 + 25) / 5 = 15
In this case, the average value of the data set is 15.
Types of Averages
There are three types of averages that are commonly used:
- Mean – The mean is the most common type of average and is calculated by adding up all the data points and dividing by the total number of data points. The mean is affected by outliers or extreme values in the data set, so it is not always the best measure of central tendency.
- Median – The median is the middle value in a data set when the values are arranged in order from smallest to largest. The median is not affected by outliers and is a good measure of central tendency for skewed data sets.
- Mode – The mode is the value that appears most frequently in a data set. The mode is a good measure of central tendency for data sets with categorical variables.
Uses of Averages
Averages are used in a variety of fields for different purposes. Some common uses of averages include:
- Analyzing financial data – Averages are often used to analyze financial data, such as stock prices, earnings, and expenses. By calculating averages, analysts can identify trends and make informed investment decisions.
- Measuring performance – Averages can be used to measure the performance of individuals or teams in different settings, such as sports, education, and business.
- Conducting research – Averages are used in research to summarize data and draw conclusions. Researchers may use different types of averages depending on the data set and research question.
Conclusion
Averages are a fundamental statistical concept that is used in a variety of fields. They provide a measure of central tendency that can help analysts and researchers understand and analyze data. There are different types of averages that can be used depending on the data set and purpose of the analysis. By understanding the basics of averages, individuals can make informed decisions and draw accurate conclusions from data.