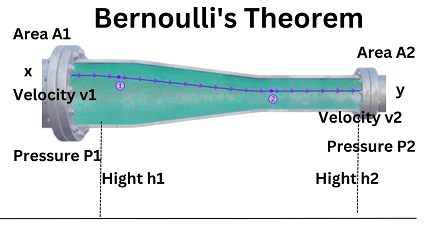
Bernoulli’s theorem, named after the Swiss mathematician Daniel Bernoulli, is a fundamental principle of fluid dynamics that describes the relationship between the pressure, velocity, and elevation of a fluid in motion. It states that as the speed of a fluid increases, the pressure within the fluid decreases, and vice versa.

In mathematical terms, Bernoulli’s theorem can be expressed as follows:

P + 1/2ρv^2 + ρgh = constant

where P is the pressure, ρ is the density of the fluid, v is the velocity of the fluid, g is the acceleration due to gravity, h is the elevation above some reference point, and the constant is the same for any point along a streamline of the fluid.

This equation shows that as the speed of the fluid increases, the pressure decreases, and vice versa. This principle is used in many applications, such as airplane wings, where the shape of the wing is designed to create different velocities of air above and below it, resulting in lift.

What is Required Bernoulli’s theorem

Bernoulli’s theorem requires certain assumptions to be true for the equation to be applicable. These assumptions are:

1. The fluid is incompressible: This means that the density of the fluid remains constant throughout the flow.
2. The flow is steady: This means that the velocity, pressure, and density of the fluid do not change with time.
3. The flow is laminar: This means that the fluid flows smoothly in parallel layers, without any turbulence.
4. There is no viscosity: This means that the fluid does not experience any frictional forces.
5. The flow is irrotational: This means that the fluid particles do not rotate about their own axes.

In practice, some of these assumptions may not hold true, but for many fluid flow problems, they are a reasonable approximation. Bernoulli’s theorem is most applicable to fluids flowing through smooth, streamlined surfaces and can be a useful tool for understanding and predicting fluid behavior.

When is Required Bernoulli’s theorem

Bernoulli’s theorem is often used in fluid dynamics to analyze the behavior of fluids in motion. It is particularly useful in situations where the flow is steady, incompressible, laminar, and irrotational, and where the fluid has a constant density.

Some common applications of Bernoulli’s theorem include:

1. Airplane wings: The shape of an airplane wing is designed to create different velocities of air above and below it, resulting in a pressure difference that creates lift.
2. Fluid flow in pipes: Bernoulli’s theorem can be used to analyze the flow of fluids in pipes and to predict pressure drops along the length of the pipe.
3. Fluid flow through nozzles: Bernoulli’s theorem can be used to analyze the behavior of fluids as they pass through nozzles and to predict the velocity and pressure of the fluid at the outlet.
4. Fluid flow over weirs and dams: Bernoulli’s theorem can be used to analyze the behavior of water as it flows over weirs and dams and to predict the velocity and pressure of the water at different points along the structure.

Overall, Bernoulli’s theorem is a valuable tool for understanding and predicting the behavior of fluids in motion, particularly in situations where the flow is relatively simple and the assumptions of the theorem are met.

Where is Required Bernoulli’s theorem

Bernoulli’s theorem can be applied to various fluid flow situations in different fields, including:

1. Aerodynamics: Bernoulli’s theorem is used to analyze the behavior of fluids, such as air, around wings, propellers, and other aerodynamic structures.
2. Hydraulics: Bernoulli’s theorem is used to analyze the flow of fluids through pipes, channels, and hydraulic structures like dams and weirs.
3. Civil engineering: Bernoulli’s theorem is used to design and analyze water distribution systems, sewage systems, and irrigation systems.
4. Biomedical engineering: Bernoulli’s theorem is used to understand and analyze the flow of blood through veins and arteries and to predict the behavior of airflows in the lungs.
5. Environmental engineering: Bernoulli’s theorem is used to design and analyze water treatment systems, wastewater treatment systems, and environmental remediation systems.

Overall, Bernoulli’s theorem has a wide range of applications in different fields where fluid dynamics plays a critical role. It is an essential tool for engineers and scientists who work with fluids and need to predict and analyze fluid behavior.

How is Required Bernoulli’s theorem

Bernoulli’s theorem can be used to analyze the behavior of fluids in motion and to predict pressure, velocity, and other properties of the fluid at different points along a flow path. The basic steps for applying Bernoulli’s theorem to a fluid flow problem are:

1. Identify the points along the flow path where you want to calculate the fluid properties, such as pressure and velocity.
2. Determine the fluid properties, such as density and viscosity, at each point along the flow path.
3. Use Bernoulli’s equation to calculate the pressure, velocity, or other fluid property at each point along the flow path.
4. Consider any assumptions made when applying Bernoulli’s theorem, such as the assumption of laminar flow or the absence of viscosity, and determine if they are valid for your particular problem.
5. Interpret the results of your calculations in light of the physical situation you are analyzing.

It is important to note that Bernoulli’s theorem is based on a set of assumptions that may not always hold true in practice. Therefore, it is essential to carefully consider the validity of these assumptions before applying the theorem and interpreting the results. In some cases, it may be necessary to use more advanced techniques, such as computational fluid dynamics, to analyze fluid behavior more accurately.

Nomenclature of Bernoulli’s theorem

Bernoulli’s theorem is expressed mathematically as follows:

P + (1/2)ρv^2 + ρgh = constant

where:

P = the static pressure of the fluid at a particular point in the flow path ρ = the density of the fluid v = the velocity of the fluid at the point of interest g = the acceleration due to gravity h = the height of the fluid above a reference point (usually the ground or a fixed reference point)

The terms in the equation have the following physical interpretations:

• The first term, P, represents the static pressure of the fluid at a particular point in the flow path.
• The second term, (1/2)ρv^2, represents the dynamic pressure of the fluid due to its motion.
• The third term, ρgh, represents the potential energy of the fluid due to its height above a reference point.

The sum of these terms is constant along a streamline, meaning that if the fluid accelerates or decelerates along the flow path, the static, dynamic, and potential pressures will adjust to maintain a constant sum.

The units of the terms in the Bernoulli’s theorem equation depend on the system of units used, but typically the pressure terms are measured in units of force per unit area (such as pascals or pounds per square inch), while the velocity terms are measured in units of length per unit time (such as meters per second or feet per second). The density term is measured in units of mass per unit volume (such as kilograms per cubic meter or pounds per cubic foot), while the height term is measured in units of length (such as meters or feet).

Case Study on Bernoulli’s theorem

One example of a case study that involves the application of Bernoulli’s theorem is the analysis of fluid flow through a pipeline system. In this scenario, Bernoulli’s theorem can be used to predict pressure drops along the length of the pipeline and to design a system that will meet the required flow rate and pressure specifications.

Consider a pipeline system that consists of a pump, a straight section of pipe, and a control valve, as shown in the diagram below:

lua
     Pump -- Pipe -- Control Valve

The pump provides a steady flow of fluid through the pipe, while the control valve regulates the flow rate by adjusting the cross-sectional area of the pipe. To analyze the behavior of the fluid in this system, we can apply Bernoulli’s theorem at two points along the flow path: one just upstream of the control valve and one just downstream of the control valve.

Assuming that the fluid is incompressible, laminar, and irrotational, and that the pipe is horizontal, we can simplify Bernoulli’s theorem to:

P1 + (1/2)ρv1^2 = P2 + (1/2)ρv2^2

where P1 and v1 are the pressure and velocity of the fluid upstream of the control valve, and P2 and v2 are the pressure and velocity of the fluid downstream of the control valve.

We can use this equation to solve for the pressure drop across the control valve, which is given by:

ΔP = P1 – P2 = (1/2)ρ(v2^2 – v1^2)

This equation tells us that the pressure drop across the control valve depends on the difference in velocity between the fluid upstream and downstream of the valve. Therefore, to maintain a constant flow rate through the system, the valve must be adjusted to ensure that the fluid velocity remains constant.

In practice, engineers use more complex models and simulations to design and optimize pipeline systems, taking into account factors such as friction losses, turbulence, and other effects that can impact fluid behavior. However, Bernoulli’s theorem provides a useful starting point for understanding the basic principles of fluid flow and can be used to develop initial designs and calculations for pipeline systems.

White paper on Bernoulli’s theorem

Introduction:

Bernoulli’s theorem is a fundamental principle of fluid mechanics that describes the relationship between fluid pressure, velocity, and potential energy in a flow system. This theorem is named after Swiss mathematician Daniel Bernoulli, who first introduced it in his book Hydrodynamica in 1738. Bernoulli’s theorem is widely used in engineering, physics, and other fields to analyze fluid flows and to design systems that rely on fluid behavior.

Statement of Bernoulli’s theorem:

Bernoulli’s theorem can be stated as follows:

“Within a steady flow of an incompressible fluid, the sum of the static pressure, dynamic pressure, and potential energy per unit volume is constant along any streamline.”

Mathematically, Bernoulli’s theorem can be expressed as:

P + (1/2)ρv^2 + ρgh = constant

where P is the static pressure of the fluid, ρ is the fluid density, v is the fluid velocity, g is the acceleration due to gravity, h is the height of the fluid above a reference point, and the constant is the same for all points along a given streamline.

Interpretation of Bernoulli’s theorem:

Bernoulli’s theorem can be interpreted as follows:

1. The sum of the static pressure, dynamic pressure, and potential energy of the fluid is constant along a streamline.
2. When the fluid velocity increases, the static pressure decreases, and vice versa.
3. When the fluid rises in a pipe or duct, its static pressure decreases, and vice versa.
4. Bernoulli’s theorem applies only to steady flow of incompressible fluids.
5. Bernoulli’s theorem is based on a set of assumptions that may not always hold true in practice, such as the assumption of laminar flow or the absence of viscosity.

Applications of Bernoulli’s theorem:

Bernoulli’s theorem has many practical applications, including:

1. Design of aircraft wings and other aerodynamic surfaces.
2. Design of fluid transport systems, such as pipelines, channels, and ducts.
3. Design of hydraulic turbines and other fluid machinery.
4. Analysis of weather patterns and ocean currents.
5. Study of blood flow in the human body.
6. Design of fountains and water jets.

Conclusion:

Bernoulli’s theorem is a fundamental principle of fluid mechanics that describes the relationship between fluid pressure, velocity, and potential energy in a flow system. This theorem is widely used in engineering, physics, and other fields to analyze fluid flows and to design systems that rely on fluid behavior. While Bernoulli’s theorem is based on a set of assumptions that may not always hold true in practice, it provides a useful starting point for understanding the basic principles of fluid flow and can be used to develop initial designs and calculations for fluid systems.