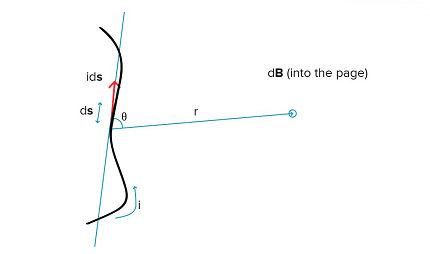
Biot-Savart’s law is a fundamental law in electromagnetism that describes the magnetic field produced by a steady current in a wire. It states that the magnetic field at a point in space due to a current-carrying wire is directly proportional to the current in the wire and the length of the wire segment, and inversely proportional to the distance from the wire.
The mathematical expression of the Biot-Savart law is given as:
d𝐵 = (𝜇0/4𝜋) (Id𝑙 x ̂)/r^2
where d𝐵 is the magnetic field at a point in space, 𝜇0 is the permeability of free space, I is the current in the wire, d𝑙 is the length element of the wire, x ̂ is a unit vector pointing in the direction of the current, and r is the distance from the wire to the point in space where the magnetic field is being measured.
The law can be used to calculate the magnetic field produced by a current-carrying wire at any point in space, and is used extensively in the analysis of magnetic fields in various applications, such as in motors, generators, and transformers.
What is Required Biot–Savart’s law
To apply Biot-Savart’s law, you need to know the following information:
- The current-carrying wire: You need to know the path of the wire through which the current flows. The wire can be straight or curved.
- The magnitude of the current: You need to know the value of the current flowing through the wire.
- The location of the point in space where the magnetic field is to be calculated: You need to know the distance and direction from the wire to the point in space where you want to determine the magnetic field.
- The length element of the wire: You need to know the differential length of the wire segment, which is used to calculate the contribution to the magnetic field at the point in space.
- The permeability of free space: This is a physical constant denoted by 𝜇0, which relates to the ability of the space to support magnetic fields.
Once you have this information, you can use the Biot-Savart law to calculate the magnetic field at any point in space due to a current-carrying wire. The law is derived from experimental observations and is valid for steady currents in conductors.
When is Required Biot–Savart’s law
Biot-Savart’s law is required in situations where you need to calculate the magnetic field produced by a current-carrying wire at a point in space. Some examples of where Biot-Savart’s law is applicable include:
- Electromagnets: Biot-Savart’s law is used to determine the magnetic field produced by an electromagnet, which consists of a coil of wire with a current flowing through it.
- Magnetic fields due to current-carrying conductors: Biot-Savart’s law is used to calculate the magnetic field produced by a current-carrying conductor, such as a wire, at any point in space. This is important in applications such as electrical motors and transformers.
- Current loops: Biot-Savart’s law can be used to calculate the magnetic field produced by a current loop, which is a closed loop of wire with a current flowing through it. This is important in the study of magnetic materials and in the design of magnetic sensors.
- Magnetic field due to a moving charge: Biot-Savart’s law can be used to calculate the magnetic field produced by a moving charge, such as an electron, as it moves through a magnetic field.
In general, Biot-Savart’s law is required in any situation where the magnetic field produced by a steady current needs to be calculated.
Where is Required Biot–Savart’s law
Biot-Savart’s law is used in a wide range of applications, including:
- Electromagnets: Biot-Savart’s law is used to calculate the magnetic field produced by an electromagnet, which is used in a variety of devices such as electric motors, generators, and transformers.
- Magnetic resonance imaging (MRI): Biot-Savart’s law is used to calculate the magnetic field produced by the radio frequency (RF) coils used in MRI machines, which create a strong magnetic field to align the magnetic moments of protons in the body.
- Particle accelerators: Biot-Savart’s law is used to calculate the magnetic field produced by the magnets used to steer and focus particle beams in accelerators such as the Large Hadron Collider (LHC).
- Geophysics: Biot-Savart’s law is used to study the Earth’s magnetic field and its variations, which are important for understanding the Earth’s interior and its geodynamo.
- Aerospace: Biot-Savart’s law is used to calculate the magnetic field produced by spacecraft and their components, which is important for designing and testing spacecraft and for understanding the interactions between spacecraft and the Earth’s magnetic field.
- Electrical power systems: Biot-Savart’s law is used to calculate the magnetic fields produced by power transmission lines and transformers, which is important for designing and maintaining electrical power systems.
In summary, Biot-Savart’s law is used in a wide range of fields and applications where the calculation of magnetic fields is important.
How is Required Biot–Savart’s law
To apply Biot-Savart’s law, you need to follow these steps:
- Identify the current-carrying wire: Determine the path of the wire through which the current flows. The wire can be straight or curved.
- Determine the magnitude of the current: Find the value of the current flowing through the wire.
- Determine the location of the point in space where the magnetic field is to be calculated: Determine the distance and direction from the wire to the point in space where you want to determine the magnetic field.
- Determine the length element of the wire: Find the differential length of the wire segment, which is used to calculate the contribution to the magnetic field at the point in space.
- Determine the permeability of free space: This is a physical constant denoted by 𝜇0, which relates to the ability of the space to support magnetic fields.
- Apply Biot-Savart’s law: Use the mathematical expression of Biot-Savart’s law to calculate the magnetic field at the point in space due to the current-carrying wire. The law is given as:
d𝐵 = (𝜇0/4𝜋) (Id𝑙 x ̂)/r^2
where d𝐵 is the magnetic field at a point in space, 𝜇0 is the permeability of free space, I is the current in the wire, d𝑙 is the length element of the wire segment, x ̂ is a unit vector pointing in the direction of the current, and r is the distance from the wire to the point in space where the magnetic field is being measured.
- Repeat steps 4-6 for all segments of the wire: If the wire is curved or has multiple segments, you need to repeat steps 4-6 for each segment of the wire and then add up the contributions to obtain the total magnetic field at the point in space.
In summary, applying Biot-Savart’s law involves identifying the current-carrying wire, determining the location and distance of the point in space where the magnetic field is to be calculated, and using the mathematical expression of the law to calculate the magnetic field at that point.
Production of Biot–Savart’s law
Biot-Savart’s law is named after Jean-Baptiste Biot and Felix Savart, who discovered the law independently in the early 19th century. The law describes the relationship between a current-carrying wire and the magnetic field it produces at a point in space.
The discovery of Biot-Savart’s law was a result of the growing interest in the study of electricity and magnetism in the 19th century. Biot and Savart were both French physicists who were working on the relationship between electricity and magnetism.
Biot was conducting experiments on the magnetic properties of materials and discovered that a magnetic needle placed near a current-carrying wire would be deflected. He realized that the current in the wire was producing a magnetic field that was interacting with the magnetic needle.
Savart, on the other hand, was studying the magnetic properties of solenoids and discovered that the magnetic field produced by a solenoid was proportional to the current flowing through it.
Together, Biot and Savart developed the law that describes the relationship between the current-carrying wire and the magnetic field it produces at a point in space. The law is now known as Biot-Savart’s law and is widely used in various fields, including electromagnetics, geophysics, and engineering.
In summary, Biot-Savart’s law was discovered by Jean-Baptiste Biot and Felix Savart in the early 19th century as a result of their experiments on the relationship between electricity and magnetism. The law describes the relationship between a current-carrying wire and the magnetic field it produces at a point in space, and it is widely used in various fields today.
Case Study on Biot–Savart’s law
One practical application of Biot-Savart’s law is in the design and analysis of magnetic devices, such as electric motors and generators. In this case study, we will discuss how Biot-Savart’s law is used to design and analyze the magnetic field in an electric motor.
An electric motor converts electrical energy into mechanical energy through the interaction of magnetic fields. The basic components of an electric motor include a stator and a rotor. The stator is a stationary part of the motor that contains the wire coils that carry the electric current. The rotor is a rotating part that contains the magnets or magnetic material.
To design an electric motor, it is necessary to determine the magnetic field produced by the current-carrying wire coils in the stator. Biot-Savart’s law is used to calculate the magnetic field at a point in space due to a current-carrying wire.
The calculation of the magnetic field in an electric motor using Biot-Savart’s law involves the following steps:
- Determine the geometry of the motor: This includes the size and shape of the stator and rotor, the number of wire coils in the stator, and the location of the wire coils.
- Determine the current in the wire coils: The current in the wire coils is determined by the power supply to the motor.
- Determine the location of the point in space where the magnetic field is to be calculated: This can be any point in the motor where the magnetic field needs to be determined, such as the air gap between the stator and the rotor.
- Determine the length element of the wire coils: The length element of the wire coils is used to calculate the contribution to the magnetic field at the point in space.
- Determine the permeability of free space: This is a physical constant that relates to the ability of the space to support magnetic fields.
- Apply Biot-Savart’s law: Use the mathematical expression of Biot-Savart’s law to calculate the magnetic field at the point in space due to the current-carrying wire coils in the stator.
- Repeat steps 4-6 for all wire coils in the stator: If the stator has multiple wire coils, it is necessary to repeat steps 4-6 for each coil and then add up the contributions to obtain the total magnetic field at the point in space.
The results of the calculation can be used to optimize the design of the motor and to analyze its performance. For example, the magnetic field can be analyzed to determine the torque produced by the motor and to identify any areas where the magnetic field is not uniform, which can cause inefficiencies and reduce the performance of the motor.
In summary, Biot-Savart’s law is used in the design and analysis of electric motors to calculate the magnetic field produced by the current-carrying wire coils in the stator. The calculation involves determining the geometry of the motor, the current in the wire coils, the location of the point in space where the magnetic field is to be calculated, and applying the mathematical expression of Biot-Savart’s law. The results of the calculation are used to optimize the design of the motor and to analyze its performance.
White paper on Biot–Savart’s law
Title: Biot-Savart’s Law: A Comprehensive Overview and Applications
Abstract:
Biot-Savart’s law is a fundamental law in electromagnetism that describes the relationship between a current-carrying wire and the magnetic field it produces at a point in space. The law has many practical applications in various fields, including engineering, geophysics, and biology. This white paper provides a comprehensive overview of Biot-Savart’s law, including its history, mathematical formulation, and practical applications.
Introduction:
Biot-Savart’s law is named after Jean-Baptiste Biot and Felix Savart, who discovered the law independently in the early 19th century. The law describes the relationship between a current-carrying wire and the magnetic field it produces at a point in space. Biot-Savart’s law is an essential law in electromagnetism, and its applications range from electric motors and generators to MRI machines and Earth’s magnetic field.
History:
The discovery of Biot-Savart’s law was a result of the growing interest in the study of electricity and magnetism in the 19th century. Biot and Savart were both French physicists who were working on the relationship between electricity and magnetism. Biot was conducting experiments on the magnetic properties of materials and discovered that a magnetic needle placed near a current-carrying wire would be deflected. He realized that the current in the wire was producing a magnetic field that was interacting with the magnetic needle. Savart, on the other hand, was studying the magnetic properties of solenoids and discovered that the magnetic field produced by a solenoid was proportional to the current flowing through it.
Mathematical Formulation:
Biot-Savart’s law is a mathematical expression that relates the magnetic field produced by a current-carrying wire to the current and the distance from the wire. The law is expressed as:
B = (μ₀ / 4π) ∫(Idl × r) / r³
where B is the magnetic field at a point in space, I is the current in the wire, dl is a length element of the wire, r is the distance from the wire to the point in space, and μ₀ is the permeability of free space. The integral is taken over the length of the wire.
Applications:
Biot-Savart’s law has many practical applications in various fields. One of the most significant applications is in the design and analysis of magnetic devices, such as electric motors and generators. Biot-Savart’s law is used to calculate the magnetic field produced by the current-carrying wire coils in the stator, which is essential for optimizing the design and analyzing the performance of the motor.
Another application of Biot-Savart’s law is in geophysics, where it is used to model the Earth’s magnetic field. The law is used to calculate the magnetic field produced by the Earth’s core, which is essential for understanding the Earth’s magnetic field and its role in the Earth’s geology.
Biot-Savart’s law is also used in medical imaging, specifically in magnetic resonance imaging (MRI) machines. MRI machines use strong magnetic fields to produce detailed images of the human body. Biot-Savart’s law is used to calculate the magnetic field produced by the coils in the MRI machine, which is essential for optimizing the design and analyzing the performance of the machine.
Conclusion:
Biot-Savart’s law is a fundamental law in electromagnetism that plays a crucial role in understanding the relationship between current-carrying wires and magnetic fields. It has a wide range of practical applications in various fields, including engineering, geophysics, and medicine. The law has been extensively studied and developed over the years, and its mathematical formulation has been refined to accurately describe the behavior of magnetic fields. Overall, Biot-Savart’s law is an essential tool for researchers and engineers working on magnetic devices, Earth’s magnetic field, and medical imaging, among other applications.