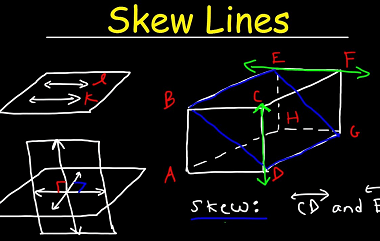
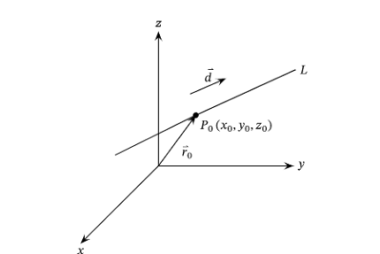
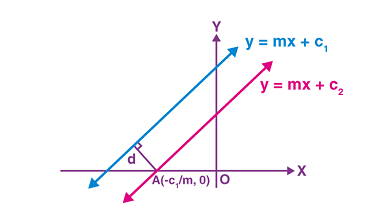Coplanar lines are lines that lie on the same plane. In other words, any two points on each of the lines can be connected with a straight line that lies entirely in the same plane. For example, if two lines intersect, they are coplanar because the plane containing one line also contains the other line.…
The angle between a line and a plane is the angle formed by the intersection of the line and the plane. This angle is measured as the acute angle between the line and the plane, i.e., the smallest angle between them. To calculate the angle between a line and a plane, you can use the…
The angle between two planes is the angle formed between their normal vectors. To find the normal vectors of two planes, you can use the cross product of their respective direction vectors. Let’s say we have two planes represented by their equations: Plane 1: ax + by + cz + d1 = 0 Plane 2:…
The angle between two lines can be found using the slope of each line. If the slopes of the lines are m1 and m2, then the angle between the lines is given by the formula: θ = arctan(|(m1 – m2)/(1 + m1*m2)|) where arctan is the inverse tangent function. Note that the absolute value is…
The distance between a point and a plane is the perpendicular distance from the point to the plane. To find the distance between a point and a plane in three-dimensional space, you can use the following formula: distance = |ax + by + cz + d| / √(a^2 + b^2 + c^2) where: To use…
The equation of a plane in three-dimensional space can be expressed in the general form: Ax + By + Cz + D = 0 where A, B, and C are the coefficients of the variables x, y, and z, respectively, and D is a constant. Alternatively, the equation of a plane can also be expressed…
The shortest distance between two lines in 3D space can be found using vector calculus. Let’s consider two non-parallel lines in 3D space: Line 1: r1 = a1 + t1 * b1 Line 2: r2 = a2 + t2 * b2 where a1 and a2 are position vectors for each line, b1 and b2 are…
Skew lines are two non-intersecting lines that are not parallel to each other. In other words, skew lines are two lines in three-dimensional space that do not lie in the same plane and do not intersect each other. Skew lines are important in geometry and can be used to solve various problems, such as finding…
In three-dimensional space, the equation of a straight line can be written in vector form as: r = a + t(b-a) where “r” is a position vector that represents any point on the line, “a” is the position vector of a known point on the line, “b” is the position vector of another known point…
Direction cosines and direction ratios are used to describe the orientation of a line or a vector in three-dimensional space. Direction cosines are the cosines of the angles that a given line or vector makes with the positive x, y, and z axes of a Cartesian coordinate system. For example, if the angles that a…
