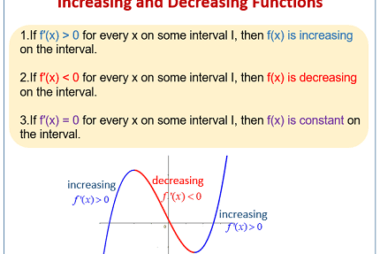
Geometric interpretation of derivatives
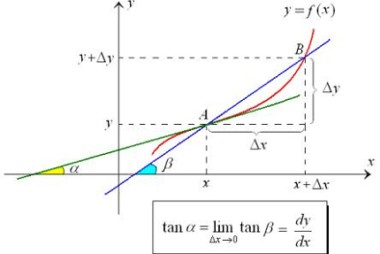
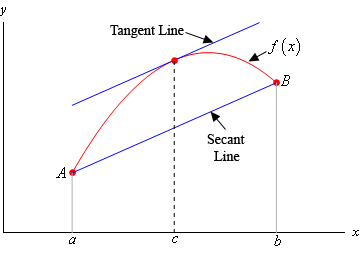
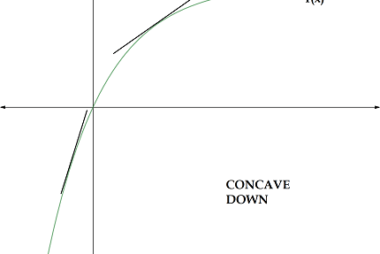
The derivative of a function can be interpreted geometrically in several ways. One common interpretation is that the derivative represents the slope of the tangent line to the graph of the function at a given point. More specifically, if we consider a function f(x) and a point (a, f(a)) on its graph, the slope of…