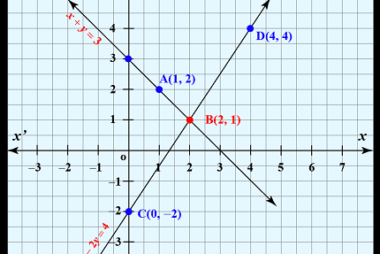
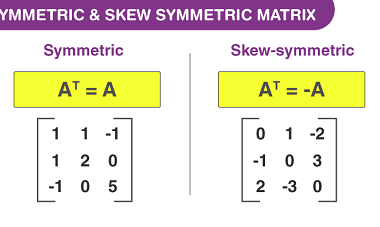
Solutions of simultaneous linear equations in two or three variables
Matrices are often used to solve systems of simultaneous linear equations in two or three variables. The matrix method involves representing the coefficients of the equations and the constants as matrices, and then performing matrix operations to obtain the solution. Let’s take an example of two linear equations in two variables: 3x + 2y =…