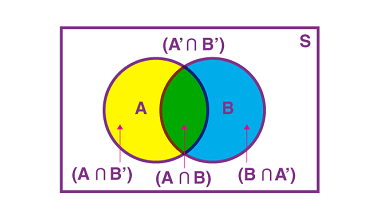
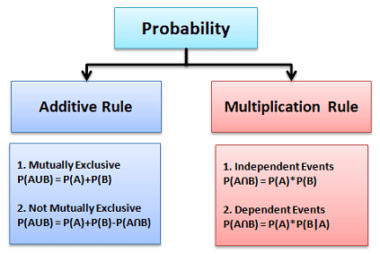
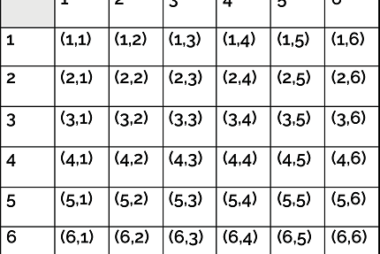
Bayes’ Theorem is a fundamental theorem in probability theory that describes the relationship between conditional probabilities. It is named after the English mathematician Thomas Bayes, who first introduced the concept in the 18th century. Bayes’ Theorem states that the probability of an event A, given that event B has occurred, is equal to the probability…
The total probability theorem is a fundamental concept in probability theory that allows us to calculate the probability of an event by conditioning on other events. The theorem states that if we have a set of events {A1, A2, A3, …, An} that are mutually exclusive and exhaustive, meaning that one and only one of…
In probability theory, two events A and B are considered independent if the occurrence of one event does not affect the probability of the other event occurring. In other words, if the probability of A occurring is not affected by whether or not B occurs, and vice versa, then A and B are independent events.…
Conditional probability is the probability of an event occurring given that another event has already occurred. It is denoted by P(A|B) and read as “the probability of A given B”. The formula for conditional probability is: P(A|B) = P(A and B) / P(B) Where P(A and B) is the probability of A and B occurring…
The addition rule of probability states that the probability of the occurrence of either of two mutually exclusive events is the sum of their individual probabilities. In other words, if A and B are two events that cannot happen simultaneously, then the probability of either A or B occurring is given by: P(A or B)…
In probability theory, a compound event is an event that consists of two or more simple events. A simple event is an event that cannot be further broken down into smaller events. There are three types of compound events: Compound events can be used to calculate the probability of complex situations, such as the probability…
In probability and statistics, events are outcomes or collections of outcomes from a random experiment. Here are some different types of events: What is Required Different types of events (Simple) In probability and statistics, it is often necessary to calculate the probability of different types of events. Here are some examples of how to calculate…
In probability theory, an impossible event is an event that cannot occur. It is a subset of the sample space that has zero probability of occurring. For example, if you roll a fair six-sided die, the event of getting a 7 is impossible, since the highest possible outcome is 6. Similarly, the event of flipping…
In probability theory, a sample space is the set of all possible outcomes of a random experiment or process. It is denoted by the symbol S and is a fundamental concept that helps to define probabilities and perform statistical analyses. For example, suppose we are rolling a six-sided die. The sample space for this experiment…
A random experiment is an experiment or process whose outcomes cannot be predicted with certainty. Instead, the outcomes are determined by chance or probability. Examples of random experiments include rolling a dice, flipping a coin, or drawing a card from a deck. Probability is the mathematical study of randomness and uncertainty. It deals with the…
