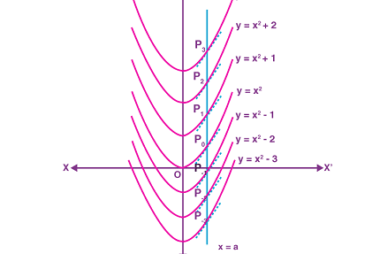
Their geometrical interpretations
Geometrical interpretations refer to the visual representation of mathematical concepts and relationships through diagrams, graphs, and other visual aids. Geometrical interpretations can help to make mathematical concepts more tangible and understandable. For example, the geometrical interpretation of slope is the steepness of a line on a graph. The slope is calculated by dividing the change…