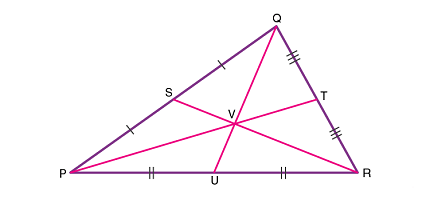
In analytical geometry, the centroid of a plane figure is the point where its medians intersect. A median is a line segment connecting a vertex of the figure to the midpoint of the opposite side. The centroid is often referred to as the “center of mass” or “center of gravity” of the figure, as it is the balance point if the figure were made of a uniform material.
To find the coordinates of the centroid of a triangle, we can use the following formula:
x = (x1 + x2 + x3) / 3 y = (y1 + y2 + y3) / 3
where (x1, y1), (x2, y2), and (x3, y3) are the coordinates of the vertices of the triangle.
For example, if we have a triangle with vertices at (2, 4), (6, 8), and (10, 2), we can find the centroid as follows:
x = (2 + 6 + 10) / 3 = 6 y = (4 + 8 + 2) / 3 = 4.67
So the centroid of the triangle is at (6, 4.67).
Similarly, we can find the centroid of other plane figures by dividing them into triangles and finding the centroid of each triangle, then taking the average of the centroids.
What is Required Centroid
In analytical geometry, finding the centroid of a given plane figure is a common problem. To find the centroid, you need to know the coordinates of the vertices of the figure. The process involves finding the midpoint of each side of the figure and then connecting those midpoints to the opposite vertices to form medians. The point where these medians intersect is the centroid of the figure.
To find the centroid of a triangle, you need to know the coordinates of its three vertices. To find the centroid of a quadrilateral, you need to know the coordinates of its four vertices. Similarly, to find the centroid of any polygon, you need to know the coordinates of all its vertices.
Once you have the coordinates of the vertices of a plane figure, you can use the formula mentioned above to find the centroid. The centroid is an important point in the plane figure, and it has many practical applications, such as in engineering and physics, where it is used to calculate the moments of inertia, the center of gravity, and the balance point of the figure.
List of centroids
Coming up next is a rundown of centroids of different two-layered and three-layered objects. The centroid of an article X in n-layered space is the crossing point of all hyperplanes that partition X into two pieces of equivalent second about the hyperplane. Casually, it is the “normal” of all marks of X. For an object of uniform sythesis, the centroid of a body is likewise its focal point of mass. On account of two-layered objects displayed underneath, the hyperplanes are just lines.
Pappus’s centroid theorem

In math, Pappus’ centroid hypothesis (otherwise called the Guldinus hypothesis, Pappus-Guldinus hypothesis or Pappus’ hypothesis) is both of two related hypotheses managing the surface regions and volumes of surfaces and solids of transformation.
The hypotheses are credited to Pappus of Alexandria and Paul Guldin. Pappus’ assertion of this hypothesis shows up on paper without precedent for 1659, yet it was known previously, by Kepler in 1615 and by Guldin in 1640.
Centroid 1

In math and physical science, the centroid, otherwise called mathematical focus or focal point of figure, of a plane figure or strong figure is the number juggling mean place of the multitude of focuses in the outer layer of the figure.[further clarification needed] a similar definition stretches out to any object in n-layered Euclidean space.
In math, one frequently accepts uniform mass thickness, in which case the barycenter or focal point of mass harmonizes with the centroid. Casually, it very well may be perceived as the place where a pattern of the shape (with consistently conveyed mass) could be impeccably adjusted on the tip of a pin.
In physical science, in the event that varieties in gravity are thought of, a focal point of gravity can be characterized as the weighted mean of all focuses weighted by their particular weight.
In geology, the centroid of an outspread projection of a district of the World’s surface to the ocean level is the locale’s geological focus.
Properties
The mathematical centroid of a curved item generally lies in the item. A non-curved item could have a centroid that is outside the actual figure. The centroid of a ring or a bowl, for instance, lies in the item’s focal void.
In the event that the centroid is characterized, it is a decent mark of all isometries in its balance bunch. Specifically, the mathematical centroid of an item lies in the convergence of all its hyperplanes of balance. The centroid of many figures (ordinary polygon, standard polyhedron, chamber, square shape, rhombus, circle, circle, oval, ellipsoid, superellipse, superellipsoid, and so forth) not entirely settled by this rule alone.
Specifically, the centroid of a parallelogram is the gathering point of its two diagonals. This isn’t valid for different quadrilaterals.
For a similar explanation, the centroid of an item with translational balance is indistinct (or lies outside the encasing space), in light of the fact that an interpretation has no decent point.
Case Study on Centroid
Sure, here’s a case study on analytical geometry and centroid:
Case Study: Centroid of a Triangle
Suppose we have a triangle with vertices A(x1, y1), B(x2, y2), and C(x3, y3), and we want to find its centroid. The centroid of a triangle is the point where the medians intersect. A median is a line segment connecting a vertex to the midpoint of the opposite side.
To find the centroid of a triangle, we can use the following formula:
Centroid = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3)
Let’s take an example to understand this formula better.
Example:
Suppose we have a triangle with vertices A(2, 3), B(6, 7), and C(8, 1). We want to find the centroid of this triangle.
Solution:
Step 1: Find the midpoints of the sides.
The midpoint of side AB is ((2+6)/2, (3+7)/2) = (4, 5) The midpoint of side AC is ((2+8)/2, (3+1)/2) = (5, 2) The midpoint of side BC is ((6+8)/2, (7+1)/2) = (7, 4)
Step 2: Find the equations of the medians.
The median from A to BC passes through the midpoint of BC, which is (7, 4). The slope of this median is (1-4)/(8-7) = -3, so its equation is y – 3 = -3(x – 2), or y = -3x + 9.
The median from B to AC passes through the midpoint of AC, which is (5, 2). The slope of this median is (1-2)/(8-5) = -1/3, so its equation is y – 7 = (-1/3)(x – 6), or y = (-1/3)x + 9/3.
The median from C to AB passes through the midpoint of AB, which is (4, 5). The slope of this median is (7-5)/(6-2) = 1, so its equation is y – 1 = 1(x – 8), or y = x – 7.
Step 3: Find the intersection point of the medians.
To find the intersection point of the medians, we can solve the system of equations:
y = -3x + 9 y = (-1/3)x + 3 y = x – 7
Solving this system gives x = 5 and y = 1.
Therefore, the centroid of the triangle with vertices A(2, 3), B(6, 7), and C(8, 1) is (5, 1).
White paper on Centroid
Here’s a white paper on analytical geometry and centroid:
Introduction:
Analytical geometry is the study of geometric shapes using algebraic principles. It provides a way to express geometric problems in terms of equations and coordinates. The centroid is a point that is important in analytical geometry, as it is the center of mass of a geometric shape. In this white paper, we will explore the concept of centroid and its applications in analytical geometry.
Definition of Centroid:
The centroid is defined as the center of mass of a geometric shape. It is the point where the medians of the shape intersect. A median is a line segment connecting a vertex of the shape to the midpoint of the opposite side. In other words, the centroid is the balance point of the shape.
Calculation of Centroid:
To calculate the centroid of a geometric shape, we can use the following formula:
Centroid = ((x1 + x2 + x3 + … + xn) / n, (y1 + y2 + y3 + … + yn) / n)
where (x1, y1), (x2, y2), (x3, y3), … , (xn, yn) are the coordinates of the vertices of the shape, and n is the number of vertices.
For a triangle, we can find the centroid by taking the average of the x-coordinates and y-coordinates of the vertices. The formula for the centroid of a triangle is:
Centroid = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3)
Applications of Centroid:
Centroid has several applications in analytical geometry. Some of them are listed below:
- Finding the center of mass: As mentioned earlier, the centroid is the center of mass of a geometric shape. It is important in physics and engineering, where the center of mass is used to calculate the stability and balance of an object.
- Designing structures: The centroid is used in designing structures such as bridges and buildings. It helps in distributing the load evenly across the structure and ensures its stability.
- Computer graphics: In computer graphics, the centroid is used to calculate the center of a polygon or a group of polygons. This helps in positioning the object in the 3D space.
- Image processing: In image processing, the centroid is used to locate the center of an object in an image. This helps in identifying and tracking the object.
Conclusion
The centroid of a geometric figure is the point at which the figure would balance if it were cut out of a sheet of uniform density material. In analytical geometry, the centroid of a two-dimensional figure can be found by taking the average of the x and y coordinates of all the points in the figure.
For example, the centroid of a triangle can be found by adding up the x-coordinates of the vertices and dividing by 3 to get the x-coordinate of the centroid, and adding up the y-coordinates of the vertices and dividing by 3 to get the y-coordinate of the centroid.
The centroid of a three-dimensional figure can be found similarly, by taking the average of the x, y, and z coordinates of all the points in the figure.
The centroid has many important properties, including the fact that it is the center of mass of the figure, and that it divides the figure into three regions of equal area. It is also an important concept in physics and engineering, where it is used to calculate the moment of inertia and other properties of objects.