The chain rule is a fundamental rule in calculus that allows you to differentiate a function that is composed of two or more functions.
More specifically, if you have a function f(x) that is composed of two functions g(x) and h(x), such that f(x) = g(h(x)), then the chain rule states that:
f'(x) = g'(h(x)) * h'(x)
In other words, to find the derivative of f(x), you first find the derivative of g(x) with respect to h(x) (i.e., g'(h(x))), and then multiply that by the derivative of h(x) with respect to x (i.e., h'(x)).
This rule is extremely useful in many areas of mathematics and science, including physics, engineering, and economics.
What is Required Chain rule
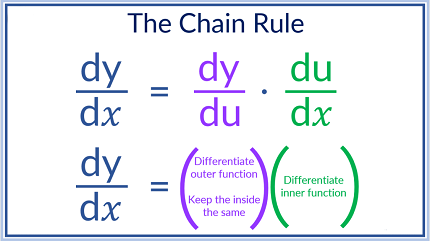
The chain rule in differential calculus is a formula for finding the derivative of a composite function. Specifically, it states that if y = f(g(x)) is a composite function, where f and g are both differentiable functions, then:
dy/dx = f'(g(x)) * g'(x)
In other words, to differentiate a composite function, you first differentiate the outer function (f) with respect to its inner variable (g(x)), and then multiply that by the derivative of the inner function (g(x)) with respect to x.
The chain rule is an important tool for solving many different types of problems in calculus, including optimization problems, related rates problems, and integration by substitution. It is also a key concept in many areas of science and engineering, including physics, chemistry, and biology.
Who is Required Chain rule
The chain rule is a fundamental concept in differential calculus and is relevant to anyone studying or working in fields that use calculus, such as mathematics, physics, engineering, economics, and more.
The concept of the chain rule was first developed by mathematicians such as Leibniz and Euler in the 18th century, and it has since become an essential tool for solving many different types of problems in calculus.
In particular, the chain rule is important for understanding and solving problems that involve composite functions, where one function is applied to the output of another function. For example, in physics, the motion of an object may be described by a composite function that involves position, velocity, and acceleration, and the chain rule is used to find the derivatives of these functions with respect to time.
Therefore, the chain rule is a fundamental concept for anyone who wants to understand and work with calculus in their academic or professional pursuits.
When is Required Chain rule
The chain rule is used whenever you need to find the derivative of a composite function, which is a function that is defined as the composition of two or more functions. In particular, the chain rule is used in situations where the output of one function is used as the input to another function.
For example, if you have a function y = f(u) and u = g(x), you can write y as a composite function of x, y = f(g(x)). To find the derivative of y with respect to x, you would need to use the chain rule.
The chain rule is also used in a variety of other situations, such as when you need to find the rate of change of a quantity that depends on another quantity that is changing, or when you need to find the slope of a tangent line to a curve that is defined by a composite function.
In general, the chain rule is a fundamental tool in differential calculus, and is used in a wide variety of applications in mathematics, science, engineering, and other fields.
Where is Required Chain rule
The chain rule is used in a wide variety of applications in mathematics, science, engineering, economics, and other fields where calculus is applied.
In mathematics, the chain rule is used extensively in differential calculus to find the derivative of composite functions, as well as in related fields such as multivariable calculus, differential geometry, and optimization.
In physics, the chain rule is used to find the derivatives of functions that describe the motion of objects, such as position, velocity, and acceleration. It is also used in thermodynamics, electromagnetism, and other areas of physics.
In engineering, the chain rule is used to find the derivatives of functions that describe physical systems, such as the flow of fluids or the behavior of mechanical systems.
In economics, the chain rule is used to analyze and model complex systems that involve multiple variables, such as supply and demand, production functions, and utility functions.
Overall, the chain rule is a fundamental tool in calculus that is used in many different areas of mathematics, science, and engineering to solve a wide range of problems and model complex systems.
How is Required Chain rule
The chain rule in differential calculus is a formula that allows you to find the derivative of a composite function. The general form of the chain rule is:
(dy/dx) = (dy/du) * (du/dx)
where y is a composite function of u, and u is a function of x.
To apply the chain rule, you need to differentiate the outer function (y) with respect to the inner variable (u), and then multiply that by the derivative of the inner function (u) with respect to x.
For example, suppose you have a composite function y = f(g(x)), where g(x) = x^2 and f(u) = sqrt(u). To find the derivative of y with respect to x, you would first find the derivative of f with respect to its variable u:
(df/du) = 1/(2*sqrt(u))
Then, you would find the derivative of g with respect to x:
(dg/dx) = 2x
Finally, you would apply the chain rule to get:
(dy/dx) = (df/du) * (dg/dx) = (1/(2*sqrt(u))) * (2x)
Substituting the expression for g(x) into this formula, you get:
(dy/dx) = (1/(2*sqrt(g(x)))) * (2x) = x/sqrt(x^2) = x/|x|
Thus, the derivative of y with respect to x is x/|x|.
Case Study on Chain rule
One practical application of the chain rule in differential calculus is in the analysis of the behavior of population growth.
Suppose we have a population of organisms that grows according to the logistic model:
dP/dt = rP(1 – P/K)
where P is the population size, t is time, r is the growth rate, and K is the carrying capacity of the environment.
We can rewrite this equation as a function of the variable u = 1 – P/K:
dP/dt = (dP/du) * (du/dt)
where (dP/du) is the derivative of P with respect to u, and (du/dt) is the derivative of u with respect to t.
Taking the derivative of u with respect to t, we get:
(du/dt) = (-dP/dt)/K
Substituting this expression for (du/dt) into the previous equation, we get:
dP/dt = (dP/du) * (-dP/dt)/K
Simplifying this expression, we get:
(dP/dt)^2 = -rP/K * (dP/du)
This is a first-order ordinary differential equation that we can solve for P as a function of t. We can use the chain rule to find the derivative of P with respect to u, and then substitute that expression into the equation to obtain a solution.
For example, suppose we have an initial population of 100 organisms, a carrying capacity of 500 organisms, and a growth rate of 0.1 organisms per day. We can use the chain rule to find the derivative of P with respect to u:
(dP/du) = d(P/K)/du = 1/K
Substituting this expression into the equation, we get:
(dP/dt)^2 = -0.1P/500 * (1/K)
Solving this equation for P as a function of t, we get:
P(t) = K / (1 + 4e^(-rt/K))
This equation describes the growth of the population over time, as a function of the initial conditions and the growth rate. The chain rule allowed us to transform the original equation into a more manageable form, which we could then solve to obtain a solution for P as a function of time.
White paper on Chain rule
Introduction:
The chain rule is a fundamental concept in differential calculus that allows you to find the derivative of a composite function. It is an essential tool in mathematics, science, engineering, and other fields where calculus is applied. In this white paper, we will provide an in-depth explanation of the chain rule, its applications, and its implications.
What is the chain rule?
The chain rule is a rule of differentiation that allows you to find the derivative of a composite function. A composite function is a function that is formed by combining two or more functions. For example, if you have a function f(x) and a function g(x), then the composite function h(x) = f(g(x)) is formed by applying g(x) to x and then applying f(x) to the result.
The chain rule states that if y is a composite function of u, and u is a function of x, then the derivative of y with respect to x can be found by multiplying the derivative of y with respect to u by the derivative of u with respect to x. Mathematically, this can be expressed as:
(dy/dx) = (dy/du) * (du/dx)
where y is a composite function of u, and u is a function of x.
The chain rule is used extensively in differential calculus to find the derivative of composite functions. It is also used in related fields such as multivariable calculus, differential geometry, and optimization.
Applications of the chain rule:
The chain rule is used in many different areas of mathematics, science, and engineering to solve a wide range of problems and model complex systems. Here are some examples of how the chain rule is used in various fields:
- Physics: The chain rule is used to find the derivatives of functions that describe the motion of objects, such as position, velocity, and acceleration. It is also used in thermodynamics, electromagnetism, and other areas of physics.
- Engineering: The chain rule is used to find the derivatives of functions that describe physical systems, such as the flow of fluids or the behavior of mechanical systems.
- Economics: The chain rule is used to analyze and model complex systems that involve multiple variables, such as supply and demand, production functions, and utility functions.
- Biology: The chain rule is used to model the behavior of biological systems, such as the growth of populations or the spread of diseases.
Implications of the chain rule:
The chain rule has several important implications in calculus and related fields. Here are some of the most significant implications of the chain rule:
- The chain rule allows you to find the derivative of a composite function by breaking it down into simpler parts. This is essential for solving complex problems that involve multiple variables and functions.
- The chain rule shows that the derivative of a composite function depends on the derivatives of its component functions. This means that small changes in one part of a composite function can have significant effects on the entire function.
- The chain rule can be used to find higher-order derivatives of composite functions, which can be useful in modeling complex systems and solving differential equations.
Conclusion:
The chain rule is a fundamental concept in differential calculus that allows you to find the derivative of a composite function. It is a powerful tool that is used in many different areas of mathematics, science, and engineering to solve a wide range of problems and model complex systems. The chain rule has several important implications in calculus and related fields, and understanding it is essential for anyone who works with calculus or mathematical modeling.
