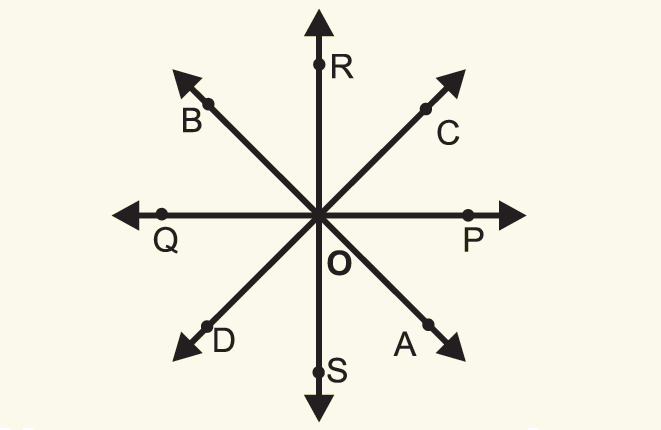
In analytical geometry, the concurrency of lines refers to the situation where three or more lines intersect at a common point.

To determine if three lines are concurrent, we can use the following method:

1. Write the equations of the lines in slope-intercept form (y = mx + b) or in point-slope form (y – y1 = m(x – x1)).
2. Set any two of the equations equal to each other and solve for x and y. This gives the point of intersection of those two lines.
3. Substitute the values of x and y into the equation of the third line. If the equation is satisfied, then the third line passes through the same point and the three lines are concurrent.

Alternatively, we can use determinants to test for concurrency. The equations of three lines can be represented by a system of three linear equations in the form ax + by = c. The coefficients a, b, and c of each equation can be arranged in a matrix and the determinant of the matrix is calculated. If the determinant is zero, then the lines are concurrent.

In general, the intersection of two lines occurs when their equations are simultaneously satisfied. However, when dealing with three or more lines, it is not always possible for all of them to intersect at a single point. In some cases, the lines may be parallel or coincident, and in these situations, they are not considered concurrent.

What is Required Concurrency of lines

To determine the concurrency of lines in analytical geometry, you need to have the equations of at least three lines. These equations can be in slope-intercept form (y = mx + b) or in point-slope form (y – y1 = m(x – x1)), or they can be represented by a system of three linear equations in the form ax + by = c.

Once you have the equations of the lines, you can use either the method of substitution or the method of determinants to test for concurrency. The method of substitution involves setting any two of the equations equal to each other and solving for x and y to find the point of intersection of those two lines. Then, you can substitute the values of x and y into the equation of the third line to check if it passes through the same point. If it does, then the three lines are concurrent.

The method of determinants involves arranging the coefficients of each equation in a matrix and calculating the determinant of the matrix. If the determinant is zero, then the lines are concurrent. This method is particularly useful when dealing with more than three lines.

In summary, to determine the concurrency of lines in analytical geometry, you need the equations of at least three lines and the knowledge of either the method of substitution or the method of determinants.

Who is Required Concurrency of lines

Analytical Geometry is a branch of mathematics that deals with the study of geometric objects using algebraic principles. The concept of concurrency of lines is an important topic in analytical geometry, and it is commonly studied in high school and college-level math courses.

Students who are studying analytical geometry, algebra, or pre-calculus may be required to learn about the concurrency of lines and how to determine if three or more lines intersect at a common point. Additionally, students who are interested in pursuing careers in fields such as engineering, architecture, or surveying may find a strong foundation in analytical geometry to be essential to their future work.

In summary, anyone who is studying mathematics, specifically analytical geometry, may be required to learn about the concurrency of lines. Additionally, those pursuing careers in related fields may find this topic to be particularly important for their work.

When is Required Concurrency of lines

The concept of concurrency of lines is typically taught in high school and college-level mathematics courses, specifically in courses that cover analytical geometry, algebra, or pre-calculus.

In high school, students usually learn about the concurrency of lines as part of their geometry curriculum. This may include learning how to find the point of intersection of two lines, and then extending that knowledge to determine if three or more lines are concurrent. Students may also learn how to use determinants to test for concurrency.

In college, the concept of concurrency of lines is typically covered in courses such as analytic geometry, linear algebra, or vector calculus. Students may learn more advanced techniques for testing for concurrency, such as using matrix methods to find the intersection point of multiple lines.

In general, the concurrency of lines is a fundamental concept in analytical geometry that is used in a variety of fields, including engineering, architecture, physics, and computer graphics. As such, it may be required knowledge for anyone pursuing a career or further study in these fields.

Where is Required Concurrency of lines

The concept of concurrency of lines is a fundamental concept in analytical geometry and is taught in mathematics courses in high schools and universities around the world. Therefore, it can be required anywhere where analytical geometry is taught as part of the curriculum.

In high schools, analytical geometry is usually a part of the mathematics curriculum and is taught in dedicated math classes. In universities, analytical geometry is typically taught as part of more advanced math courses such as calculus, linear algebra, or differential equations.

In addition to being taught in schools and universities, the concept of concurrency of lines is also used in various fields of science and engineering. For example, it is used in computer graphics to create realistic 3D models, in architecture to design and plan buildings, and in surveying to determine the positions of points on the Earth’s surface.

Therefore, the concept of concurrency of lines is required in a wide range of contexts, including mathematics education, scientific research, and practical applications in various fields.

How is Required Concurrency of lines

The concurrency of lines in analytical geometry can be determined using different methods depending on the situation. Here are two common methods:

1. Method of substitution: This method involves finding the point of intersection of any two of the given lines and then checking if the third line also passes through that same point. The steps are:

• Write the equations of the three lines in slope-intercept or point-slope form.
• Choose any two of the equations and set them equal to each other to find the point of intersection of those two lines.
• Substitute the values of x and y of the intersection point into the equation of the third line. If the equation is satisfied, then the three lines are concurrent.

2. Method of determinants: This method involves using a matrix of coefficients to determine if the three lines are concurrent. The steps are:

• Write the equations of the three lines in the form ax + by = c, where a, b, and c are constants.
• Form a matrix of coefficients, where the coefficients of x in the first column, the coefficients of y in the second column, and the constants in the third column.
• Calculate the determinant of the matrix. If the determinant is zero, then the three lines are concurrent.

These methods are based on the fact that three non-parallel lines in a plane intersect at a common point. If three lines are concurrent, it means that they intersect at a single point, and this point can be found by solving any two of the equations for the point of intersection.

Case Study on Concurrency of lines

Case Study: Concurrency of Lines in Architecture

The concept of concurrency of lines in analytical geometry is an essential tool used in architecture to design and construct buildings. One example of how architects use the concept of concurrency of lines is in the design of a roof.

Consider the design of a simple gable roof, which has two sloping sides that meet at a ridge. The ridge is supported by a ridge beam, which is held up by two walls or supports on either side of the roof. To ensure that the ridge beam is level and that the roof will not collapse, the two walls or supports must be parallel, and the ridge beam must be perpendicular to them.

To achieve this, architects use the concept of concurrency of lines. They first draw a plan of the building and mark the locations of the walls or supports. Then, they draw the elevation of the roof and mark the ridge beam’s location. They draw lines from the ridge beam’s ends to the walls or supports, and they need to check that these lines are concurrent or meet at a common point.

Architects can use the method of substitution to test for concurrency. They find the equations of the lines representing the ridge beam and the two supports and solve any two of them to find the intersection point. They then check if the third line passes through that point. If it does, the lines are concurrent, and the ridge beam is perpendicular to the supports.

Another application of concurrency of lines in architecture is in the design of the structural framework of a building. Architects use the concept to ensure that the beams and columns intersect at a common point, ensuring the structural integrity of the building.

In summary, architects use the concept of concurrency of lines in analytical geometry to design and construct buildings that are structurally sound and aesthetically pleasing. They use methods such as substitution and determinants to ensure that the lines intersect at a common point, allowing them to design structures that are safe and stable.

White paper on Concurrency of lines

Introduction:

Analytical geometry is a branch of mathematics that deals with the study of geometry using algebraic principles. It is a powerful tool for analyzing and solving problems related to geometry, especially in higher dimensions. One of the important topics in analytical geometry is the study of lines and their intersection. In this white paper, we will discuss the concurrency of lines, which refers to the property of three or more lines intersecting at a single point.

Concurrency of Lines:

In analytical geometry, the concept of concurrency of lines refers to the situation where three or more lines intersect at a single point. The point of intersection is known as the point of concurrency. The idea of concurrency is essential in many areas of mathematics and has practical applications in engineering, physics, and computer science.

Conditions for Concurrency:

To determine whether three or more lines are concurrent, we need to examine their equations. If the equations of three or more lines are given in the form of Ax + By + C = 0, we can use the following conditions to determine if they are concurrent:

1. Non-parallel lines: If the three or more lines are not parallel, then they will intersect at some point. Thus, they are concurrent.
2. Two lines are parallel: If two of the lines are parallel, then they will never intersect. Thus, the three or more lines cannot be concurrent.
3. All lines are parallel: If all the lines are parallel, they will never intersect. Therefore, they cannot be concurrent.
4. All lines pass through the same point: If the equations of the lines satisfy a common point, then they will intersect at that point. Thus, they are concurrent.

Methods for Finding Point Concurrency:

To determine the point of concurrency of lines, you can use various methods, including:

1. Graphical Method: In this method, you can draw the lines on a coordinate plane and visually locate their intersection point, which is the point of concurrency.
2. Using Cramer’s Rule: Cramer’s rule is a formula that can be used to solve a system of linear equations. For three lines, each represented by an equation in standard form (Ax + By = C), you can use Cramer’s rule to find the point of concurrency by solving for the variables x and y.
3. Using Elimination Method: The elimination method involves eliminating one of the variables in the system of equations by adding or subtracting equations. For three lines, you can eliminate one variable and solve for the other variable to find the point of concurrency.
4. Using Determinants: Determinants are used to solve a system of linear equations. For three lines, you can use determinants to find the point of concurrency by setting up a matrix of coefficients and solving for the variables x and y.
5. Using Vector Method: You can represent each line as a vector and find the cross product of any two of the lines. The resulting vector is perpendicular to both lines, and the point of concurrency is the intersection point of this vector with the third line.

These methods can help you find the point of concurrency of lines. However, depending on the situation and the given information, some methods may be more suitable or efficient than others.

Conclusion:

In geometry, the point of concurrency of lines refers to the point at which three or more lines intersect. This point is significant because it is the only point that lies on all of the lines simultaneously. There are different methods that can be used to find the point of concurrency of lines, including graphical, algebraic, and vector methods. These methods involve solving systems of equations or manipulating vectors to determine the intersection point of the lines. The point of concurrency is used in various applications, such as in trilateration, which is used in GPS navigation and surveying, and in the calculation of circumcenters and centroids in triangles.