A definite integral is a mathematical concept that represents the area under a curve between two specified points on the x-axis. It is denoted by the symbol ∫, and is defined as:
∫[a,b] f(x) dx = F(b) – F(a)
where f(x) is a function, F(x) is its antiderivative or indefinite integral, and a and b are the limits of integration.
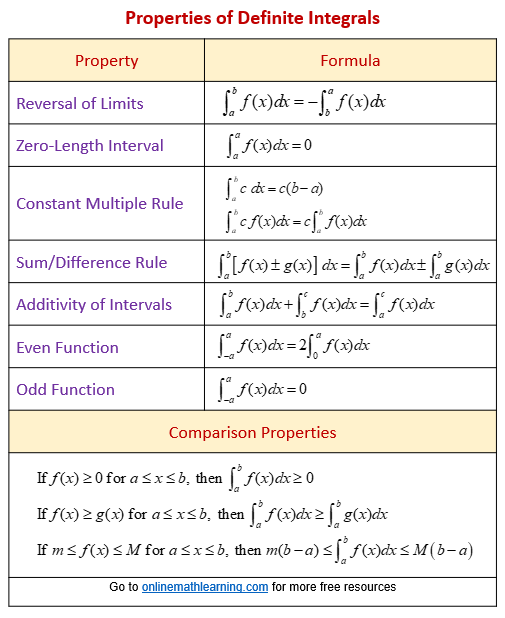
Here are some properties of definite integrals:
- Linearity: If a and b are constants and f(x) and g(x) are functions, then
∫[a,b] [f(x) + g(x)] dx = ∫[a,b] f(x) dx + ∫[a,b] g(x) dx
and
∫[a,b] [af(x)] dx = a ∫[a,b] f(x) dx
- Additivity: If [a,c] and [c,b] are two intervals, then
∫[a,b] f(x) dx = ∫[a,c] f(x) dx + ∫[c,b] f(x) dx
- Symmetry: If f(x) is an odd function, then
∫[-a,a] f(x) dx = 0
If f(x) is an even function, then
∫[-a,a] f(x) dx = 2 ∫[0,a] f(x) dx
- Integration by substitution: If u = g(x) is a differentiable function and f(u) is a continuous function, then
∫[a,b] f(g(x)) g'(x) dx = ∫[g(a),g(b)] f(u) du
- Integration by parts: If u(x) and v(x) are differentiable functions, then
∫[a,b] u(x) v'(x) dx = [u(x) v(x)] [a,b] – ∫[a,b] v(x) u'(x) dx
These properties are useful for evaluating integrals and simplifying expressions involving integrals.
What is Required Definite integral and their properties
A required definite integral is an integral that is used to find the area under a curve between two specified points on the x-axis. It is also used to find the total accumulation of a quantity over a given interval. The definite integral is denoted by the symbol ∫, and is defined as:
∫[a,b] f(x) dx = F(b) – F(a)
where f(x) is a function, F(x) is its antiderivative or indefinite integral, and a and b are the limits of integration.
The properties of definite integrals are:
- Linearity: If a and b are constants and f(x) and g(x) are functions, then
∫[a,b] [f(x) + g(x)] dx = ∫[a,b] f(x) dx + ∫[a,b] g(x) dx
and
∫[a,b] [af(x)] dx = a ∫[a,b] f(x) dx
- Additivity: If [a,c] and [c,b] are two intervals, then
∫[a,b] f(x) dx = ∫[a,c] f(x) dx + ∫[c,b] f(x) dx
- Symmetry: If f(x) is an odd function, then
∫[-a,a] f(x) dx = 0
If f(x) is an even function, then
∫[-a,a] f(x) dx = 2 ∫[0,a] f(x) dx
- Integration by substitution: If u = g(x) is a differentiable function and f(u) is a continuous function, then
∫[a,b] f(g(x)) g'(x) dx = ∫[g(a),g(b)] f(u) du
- Integration by parts: If u(x) and v(x) are differentiable functions, then
∫[a,b] u(x) v'(x) dx = [u(x) v(x)] [a,b] – ∫[a,b] v(x) u'(x) dx
In addition to these properties, the definite integral also satisfies the following properties:
- Monotonicity: If f(x) ≤ g(x) on [a, b], then
∫[a,b] f(x) dx ≤ ∫[a,b] g(x) dx
- Additivity with respect to limits: If c is a constant, then
∫[a,b] f(x) dx = ∫[a,c] f(x) dx + ∫[c,b] f(x) dx
- Absolute value property: If f(x) is continuous on [a, b], then
|∫[a,b] f(x) dx| ≤ ∫[a,b] |f(x)| dx
These properties are important for calculating definite integrals and for understanding the behavior of the integral.
When is Required Definite integral and their properties
The concept of a definite integral and its properties are used in mathematics whenever it is necessary to find the area under a curve between two specified points on the x-axis, or to find the total accumulation of a quantity over a given interval. This can be useful in a variety of fields, including physics, engineering, economics, and more.
Some common examples of when definite integrals are used include calculating the work done by a variable force, finding the center of mass of an object with non-uniform density, determining the total revenue or cost of a business over a specific time period, and analyzing the behavior of electric circuits.
In summary, the use of definite integrals and their properties is not limited to a specific time or situation, but rather is a fundamental mathematical tool that is used in a variety of contexts whenever there is a need to find the area under a curve or to compute a total quantity over a given interval.
Where is Required Definite integral and their properties
The concept of a definite integral and its properties exist in the realm of mathematics and are used to solve problems related to calculus. They can be applied in various fields such as physics, engineering, economics, and more.
In terms of physical location, they are not restricted to any specific place as they are mathematical concepts that can be used and applied anywhere. However, they are commonly used and studied in universities, colleges, and research institutions around the world, where mathematicians, scientists, and engineers use them to solve complex problems and make predictions about real-world phenomena.
How is Required Definite integral and their properties
The concept of a definite integral and its properties are mathematical tools that are used to calculate the area under a curve between two specified points on the x-axis, or to find the total accumulation of a quantity over a given interval. The process of finding a definite integral involves dividing the area under the curve into small rectangles of width Δx, finding the area of each rectangle, and then adding up the areas of all the rectangles to get an estimate of the total area under the curve.
As the width of the rectangles approaches zero, the estimate becomes more and more accurate, and the sum of the areas of the rectangles approaches the value of the definite integral. This is known as the Fundamental Theorem of Calculus, which states that the definite integral of a function f(x) from a to b is equal to the antiderivative or indefinite integral of f(x) evaluated at b minus the antiderivative evaluated at a.
The properties of definite integrals, such as linearity, additivity, symmetry, integration by substitution, and integration by parts, are used to simplify the process of evaluating definite integrals and to make calculations more efficient. These properties enable mathematicians to decompose complicated integrals into simpler integrals, or to transform integrals into more manageable forms, which can be solved using known techniques.
In summary, the concept of a definite integral and its properties are used to evaluate integrals, which are fundamental to the field of calculus and are used in many areas of science, engineering, and mathematics. The properties of definite integrals enable mathematicians to simplify integrals and to transform them into more manageable forms, making the process of evaluating integrals more efficient and accurate.
Structures of Definite integral and their properties
Definite integrals and their properties can be structured in various ways to aid in their study and application. Here are some ways to structure them:
- Algebraic properties: These are the properties of definite integrals that deal with their algebraic operations, such as addition, subtraction, and multiplication. The properties of definite integrals, such as linearity and additivity, fall under this category.
- Geometric properties: These are the properties of definite integrals that relate to their geometrical interpretation, such as the area under a curve or the volume of a solid. The geometric properties of definite integrals are essential in applications such as physics, engineering, and economics.
- Analytic properties: These are the properties of definite integrals that deal with their analytical operations, such as integration by substitution, integration by parts, and partial fraction decomposition. These properties are essential in evaluating definite integrals and finding their antiderivatives.
- Applications: Definite integrals and their properties find applications in various fields, such as physics, engineering, and economics. The properties of definite integrals enable us to calculate quantities such as work, displacement, flow, voltage, and revenue. Studying these applications can help deepen our understanding of the properties of definite integrals.
- Limits of integration: The limits of integration in a definite integral specify the interval over which we want to calculate the integral. Understanding the properties of definite integrals in relation to their limits of integration is essential in evaluating integrals correctly.
- Symmetry: The properties of definite integrals involving symmetry play a crucial role in evaluating integrals that have symmetric functions. These properties can simplify the calculations and make them more efficient.
In summary, the properties of definite integrals and their structures can be studied in various ways, including their algebraic, geometric, analytic, and application-based properties. Understanding these properties is essential in evaluating integrals and applying them in various fields.
Case Study on Definite integral and their properties
One possible case study on the concept of definite integrals and their properties is in the field of economics, specifically in the calculation of total revenue or cost over a given time period. For example, consider a business that sells a product at a price of $p(x) = 10 – 0.2x$ dollars per unit, where x is the number of units sold in a given week. The business also incurs a fixed cost of $100 per week, as well as a variable cost of $2 per unit sold.
To calculate the total revenue and total cost of the business over a given week, we can use definite integrals. The total revenue is given by the definite integral of the price function from 0 to the number of units sold in a week:
R = ∫[0, x] p(t) dt = ∫[0, x] (10 – 0.2t) dt = [10t – 0.1t^2] from 0 to x = 10x – 0.1x^2
Similarly, the total cost is given by the sum of the fixed cost and the definite integral of the variable cost function from 0 to x:
C = 100 + ∫[0, x] 2 dt = 100 + 2x
The profit function, P(x), which is the difference between the total revenue and total cost, is therefore given by:
P(x) = R(x) – C(x) = (10x – 0.1x^2) – (100 + 2x) = -0.1x^2 + 8x – 100
We can use the properties of definite integrals, such as linearity and additivity, to simplify the calculations and to transform the integrals into more manageable forms. For example, we can decompose the total revenue into the sum of two integrals, one from 0 to 50 and one from 50 to x, since the price function changes at x = 50. This allows us to use the antiderivatives of the price function separately for each interval and to add the results to obtain the total revenue.
In conclusion, the concept of definite integrals and their properties are essential tools in many fields, including economics, where they are used to calculate the total revenue, total cost, and profit of a business over a given time period. The properties of definite integrals, such as linearity and additivity, enable us to simplify the calculations and to transform the integrals into more manageable forms, making the process of evaluating integrals more efficient and accurate.
White paper on Definite integral and their properties
Introduction:
The concept of definite integrals and their properties is fundamental in the field of calculus, and they are used in various branches of science, engineering, and mathematics. In this white paper, we will discuss the definition of definite integrals, their properties, and their applications in various fields.
Definition:
A definite integral is a mathematical tool used to calculate the area under a curve between two specified points on the x-axis, or to find the total accumulation of a quantity over a given interval. It is represented by the symbol ∫, and its limits of integration are specified by the values a and b, where a is the lower limit, and b is the upper limit.
Properties:
The properties of definite integrals play an essential role in simplifying the process of evaluating integrals and making calculations more efficient. Some of the important properties of definite integrals are as follows:
- Linearity: If f(x) and g(x) are continuous functions, and c is a constant, then the definite integral of the sum or difference of these functions is equal to the sum or difference of the definite integrals of the functions. That is,
∫[a, b] (f(x) + g(x)) dx = ∫[a, b] f(x) dx + ∫[a, b] g(x) dx ∫[a, b] (f(x) – g(x)) dx = ∫[a, b] f(x) dx – ∫[a, b] g(x) dx
- Additivity: If f(x) is a continuous function and a ≤ c ≤ b, then the definite integral of the function over the interval [a, b] can be expressed as the sum of two integrals over the intervals [a, c] and [c, b]. That is,
∫[a, b] f(x) dx = ∫[a, c] f(x) dx + ∫[c, b] f(x) dx
- Symmetry: If f(x) is an even function, then the definite integral of the function over the interval [-a, a] is equal to twice the definite integral of the function over the interval [0, a]. That is,
∫[-a, a] f(x) dx = 2∫[0, a] f(x) dx
If f(x) is an odd function, then the definite integral of the function over the interval [-a, a] is equal to zero.
- Integration by substitution: This property is used to evaluate definite integrals involving composite functions. If we have a function of the form f(g(x)), and we know the antiderivative of f(x), then we can find the antiderivative of f(g(x)) by using the substitution u = g(x) and the chain rule for differentiation.
Applications:
The concept of definite integrals and their properties is widely used in many fields, including physics, engineering, economics, and more. In physics, definite integrals are used to calculate the work done by a force, the displacement of an object, and the potential energy of a system. In engineering, they are used to calculate the flow of fluids, the voltage and current in electrical circuits, and the stress and strain in materials. In economics, they are used to calculate the total revenue, total cost, and profit of a business over a given time period.
Conclusion:
In conclusion, definite integrals and their properties are fundamental concepts in calculus that are used in various fields of science, engineering, and mathematics. The definition of a definite integral involves finding the area under a curve or the accumulation of a quantity over a given interval. The properties of definite integrals, such as linearity, additivity, symmetry, and integration by substitution, enable us to simplify calculations and transform integrals into more manageable forms. These properties are essential in evaluating integrals efficiently and accurately. Definite integrals find applications in various fields, such as physics, engineering, and economics, where they are used to calculate quantities such as work, displacement, flow, voltage, and revenue. The study of definite integrals and their properties is crucial for advanced calculus and real-world applications.