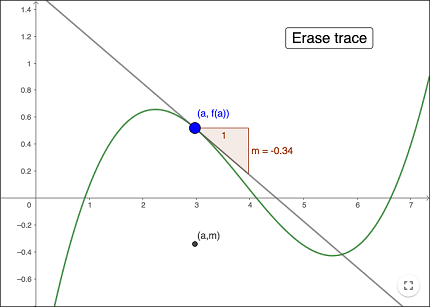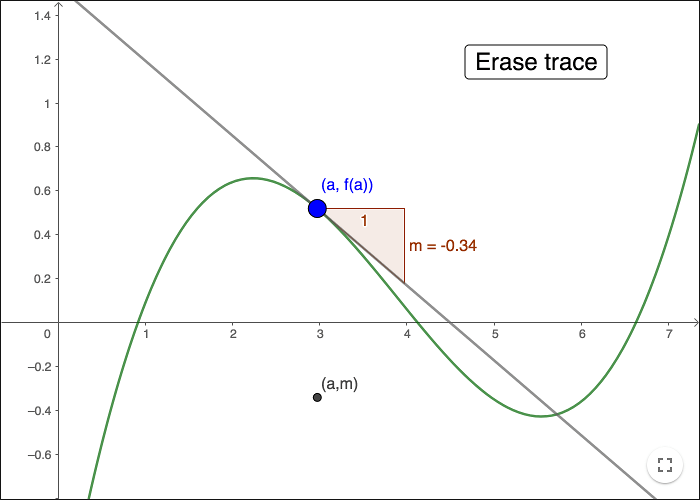
The derivative of a function represents the rate at which the function changes at each point. It is defined as the limit of the difference quotient as the distance between two points on the function approaches zero. The derivative of a function f(x) with respect to x is denoted as f'(x) or df/dx.
The formula for the derivative of a function f(x) is given by:
f'(x) = lim(h->0) [f(x+h) – f(x)]/h
This formula represents the change in f(x) for a small change in x (h). The limit as h approaches zero represents the instantaneous rate of change of f(x) at a given point x.
The derivative can also be found using the power rule, product rule, quotient rule, or chain rule, depending on the form of the function. Each rule provides a shortcut method for finding the derivative of a function without having to use the definition of the limit.
Overall, the derivative of a function is an important concept in calculus and is used in many areas of mathematics, physics, engineering, and other sciences.
What is Required Derivative of a function
The required differential calculus derivative of a function represents the rate at which the function changes with respect to its independent variable. In other words, it measures the instantaneous rate of change of the function at a specific point. The derivative is an important tool in calculus and is used in a wide range of applications in mathematics, physics, engineering, and other sciences.
To find the derivative of a function using differential calculus, we use the limit definition of the derivative. The derivative of a function f(x) with respect to x is denoted by f'(x) or dy/dx, and is defined by the following limit:
f'(x) = lim(h->0) [f(x+h) – f(x)]/h
This limit represents the slope of the tangent line to the graph of the function at the point (x,f(x)). We can also use differentiation rules such as the power rule, product rule, quotient rule, and chain rule to find the derivative of more complex functions.
The derivative of a function gives us information about the behavior of the function, such as its rate of change, its maximum and minimum points, and its concavity. It is an essential concept in calculus and is used to solve many problems in various fields of science and engineering.
Who is Required Derivative of a function
“Required Differential Calculus Derivative of a function” is not a person, but a mathematical concept used in calculus. The derivative of a function is a measure of how the function changes with respect to its independent variable, and is an important concept in differential calculus.
The concept of derivatives was first introduced by Isaac Newton and Gottfried Leibniz in the 17th century, and has since been used extensively in mathematics, physics, engineering, and other fields. The derivative is used to solve problems related to rates of change, optimization, curve sketching, and many other applications.
In calculus, the derivative of a function is denoted by f'(x) or dy/dx, and is defined as the limit of the difference quotient as the distance between two points on the function approaches zero. The derivative provides us with information about the behavior of the function, such as its slope, concavity, and inflection points.
Overall, the derivative is a fundamental concept in calculus and is used in a wide range of applications in science, technology, and engineering.
When is Required Derivative of a function
The concept of “Required Differential Calculus Derivative of a function” is always applicable in calculus whenever we need to calculate the rate of change of a function with respect to its independent variable at a particular point.
For example, in physics, we may need to calculate the velocity or acceleration of an object at a specific time, which can be done by taking the derivative of the object’s position or velocity function, respectively. In economics, we may need to calculate the marginal cost or revenue of a product, which can be done by taking the derivative of the cost or revenue function, respectively.
The derivative is also used to find maximum and minimum points of a function, which can be used to optimize various processes in science, engineering, and economics. The concept of the derivative is a fundamental tool in calculus, and it is used in a wide range of applications in various fields of science and engineering.
Therefore, the concept of “Required Differential Calculus Derivative of a function” is applicable whenever we need to analyze the behavior of a function and understand how it changes with respect to its independent variable.
Where is Required Derivative of a function
The concept of “Required Differential Calculus Derivative of a function” is a mathematical concept and is not restricted to any specific location. It is used in calculus, which is a branch of mathematics, and is applicable in various fields of science, engineering, economics, and other disciplines.
The derivative of a function is a measure of how the function changes with respect to its independent variable at a particular point. It provides information about the behavior of the function, such as its slope, concavity, and inflection points. The derivative is used in various applications such as optimization, curve sketching, and rates of change.
The concept of the derivative can be found in many different locations, such as in textbooks, online resources, research papers, and academic journals. It is also taught in various educational institutions, such as universities, colleges, and high schools, as part of calculus courses.
In summary, the concept of “Required Differential Calculus Derivative of a function” is not restricted to any specific location, but rather is a fundamental concept used in calculus and is applicable in various fields of science, engineering, economics, and other disciplines.
How is Required Derivative of a function
The “Required Differential Calculus Derivative of a function” can be calculated using the techniques and rules of differential calculus. To find the derivative of a function f(x), we use the limit definition of the derivative or apply differentiation rules such as the power rule, product rule, quotient rule, and chain rule.
The limit definition of the derivative of a function f(x) with respect to x is given by:
f'(x) = lim(h->0) [f(x+h) – f(x)]/h
This limit represents the slope of the tangent line to the graph of the function at the point (x,f(x)). We can use this definition to find the derivative of a function at a specific point.
Alternatively, we can use differentiation rules to find the derivative of more complex functions. For example, the power rule states that the derivative of a function f(x) = x^n, where n is any constant, is given by:
f'(x) = nx^(n-1)
Other rules such as the product rule, quotient rule, and chain rule can be used to find the derivative of functions that are products, quotients, or composed of other functions.
Overall, the “Required Differential Calculus Derivative of a function” can be calculated using the techniques and rules of differential calculus, which provide a powerful tool for analyzing the behavior of functions and solving problems in various fields of science, engineering, economics, and other disciplines.
Case Study on Derivative of a function
Case Study: Finding the Derivative of a Polynomial Function
Let’s consider the function f(x) = 3x^2 – 2x + 1. We want to find the derivative of this function, which represents the rate of change of the function with respect to x.
To find the derivative of f(x), we can use the power rule of differentiation, which states that if f(x) = x^n, then f'(x) = nx^(n-1). Using this rule, we can find the derivative of each term in f(x) separately and add them up to get the derivative of the whole function.
So, let’s find the derivative of each term in f(x):
f'(x) = d/dx [3x^2] – d/dx [2x] + d/dx [1]
Using the power rule, we have:
f'(x) = 6x – 2
Therefore, the derivative of f(x) is f'(x) = 6x – 2.
Now, we can use this derivative to analyze the behavior of the function f(x). For example, we can find the critical points of the function, which are the points where the derivative is zero or undefined.
Setting the derivative equal to zero, we get:
6x – 2 = 0
Solving for x, we have:
x = 1/3
Therefore, the critical point of the function is x = 1/3.
We can also find the interval where the function is increasing or decreasing by analyzing the sign of the derivative. If f'(x) > 0, then f(x) is increasing, and if f'(x) < 0, then f(x) is decreasing.
Since f'(x) = 6x – 2, we can see that f'(x) > 0 when x > 1/3, which means that f(x) is increasing on the interval (1/3, infinity). Similarly, f'(x) < 0 when x < 1/3, which means that f(x) is decreasing on the interval (-infinity, 1/3).
In conclusion, the derivative of a polynomial function can be found using the power rule of differentiation, and it provides important information about the behavior of the function such as critical points and intervals of increase or decrease. The techniques of differential calculus, including finding derivatives, are widely used in many fields, including physics, engineering, economics, and more.
White paper on Derivative of a function
Introduction:
Differential calculus is a branch of calculus that deals with the study of rates of change and slopes of curves. The derivative is a fundamental concept in differential calculus, and it represents the rate of change of a function with respect to its independent variable. In this white paper, we will discuss the concept of “Differential Calculus Derivative of a function”, its properties, and its applications in various fields.
Definition:
The derivative of a function f(x) at a point x is defined as the limit of the ratio of the change in f(x) to the change in x as the change in x approaches zero. This limit is denoted by f'(x), and it represents the instantaneous rate of change of the function at the point x.
f'(x) = lim(h->0) [f(x+h) – f(x)]/h
The derivative of a function f(x) can also be defined using the differential operator d/dx, which represents the limit as h approaches zero of (f(x+h) – f(x))/h, and is written as:
f'(x) = d/dx [f(x)]
Properties:
The derivative of a function has several properties that are useful in its calculation and analysis:
- The derivative of a constant function is zero, since the function does not change with respect to its independent variable.
- The derivative of a power function f(x) = x^n is given by:
f'(x) = nx^(n-1)
- The derivative of a sum or difference of functions is the sum or difference of their derivatives, respectively.
- The product rule of differentiation states that the derivative of the product of two functions u(x) and v(x) is given by:
(uv)’ = u’v + uv’
- The quotient rule of differentiation states that the derivative of the quotient of two functions u(x) and v(x) is given by:
(u/v)’ = (u’v – uv’)/v^2
Applications:
The concept of Differential Calculus Derivative of a function has numerous applications in various fields, including physics, engineering, economics, and more. Some of the applications are as follows:
- Optimization: Derivatives are used to find the maximum and minimum values of functions, which are important in optimization problems. For example, in economics, derivatives are used to find the optimal production level of a company that maximizes its profit.
- Rates of Change: Derivatives are used to calculate rates of change of quantities, such as velocity, acceleration, and growth rates, which are important in physics, biology, and other fields.
- Curve Sketching: Derivatives are used to sketch the graph of a function by determining its increasing and decreasing intervals, maximum and minimum points, and concavity.
- Differential Equations: Derivatives are used to solve differential equations, which are important in physics, engineering, and other fields.
Conclusion:
Differential Calculus Derivative of a function is a fundamental concept in calculus, and it represents the instantaneous rate of change of a function with respect to its independent variable. The derivative has numerous properties and applications in various fields, including optimization, rates of change, curve sketching, and differential equations. The techniques of differential calculus, including finding derivatives, are widely used in many fields, making them an essential tool for scientists, engineers, economists, and other professionals.