The derivative of a function f(x) gives the rate of change of f(x) with respect to x. The derivative of order two, or the second derivative of f(x), represents the rate of change of the first derivative of f(x) with respect to x. Mathematically, the second derivative of f(x) is denoted as f”(x) or d^2/dx^2 f(x).
To find the second derivative of a function, we need to differentiate the first derivative of the function. For example, if we have a function f(x), its first derivative is f'(x), which is the rate of change of f(x) with respect to x. To find the second derivative of f(x), we differentiate f'(x) with respect to x:
f”(x) = d/dx (f'(x)) = d/dx (d/dx f(x))
We can also express the second derivative using the Leibniz notation:
f”(x) = d^2/dx^2 f(x)
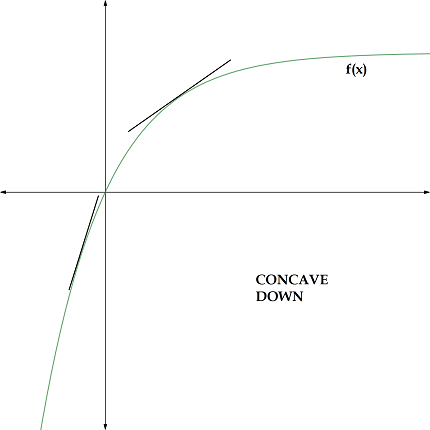
The second derivative can be used to analyze the behavior of a function, such as finding the maximum and minimum points or the points of inflection. For example, if the second derivative is positive at a point x, it indicates that the function is concave up at that point and has a minimum value at x. Conversely, if the second derivative is negative at a point x, the function is concave down at that point and has a maximum value at x. If the second derivative is zero at a point x, it may indicate a point of inflection, where the concavity of the function changes.
What is Required Derivatives of order two
In differential calculus, the second derivative or the derivative of order two is an important concept. To find the second derivative of a function, we need to differentiate the first derivative of the function with respect to the independent variable.
Suppose we have a function f(x), then its first derivative or the derivative of order one is given by:
f'(x) = df(x)/dx
To find the second derivative or the derivative of order two, we differentiate f'(x) with respect to x, which gives:
f”(x) = d^2f(x)/dx^2
The second derivative of a function gives information about the concavity of the function. If the second derivative is positive, the function is said to be concave up, and if the second derivative is negative, the function is said to be concave down. The points where the second derivative is zero are called inflection points, where the concavity of the function changes.
In addition to finding the second derivative, we can also find higher-order derivatives of a function by differentiating the lower-order derivatives with respect to the independent variable. For example, the third derivative of a function is the derivative of the second derivative, which is given by:
f”'(x) = d^3f(x)/dx^3
In general, the nth derivative of a function is given by:
f^(n)(x) = d^n f(x)/dx^n
where n is a positive integer. The nth derivative gives information about the rate of change of the (n-1)th derivative of the function.
Who is Required Derivatives of order two
The concept of derivatives of order two, or the second derivative, is important in the field of calculus and is required for anyone studying or working in a field that uses calculus, such as mathematics, physics, engineering, economics, and many others.
In mathematics, the second derivative is used in the study of functions, particularly in analyzing the curvature and concavity of a function, and in optimization problems such as finding maximum and minimum values.
In physics, the second derivative is used to study motion and acceleration, such as determining the velocity and acceleration of a moving object.
In engineering, the second derivative is used in the design and analysis of systems, such as in control systems, signal processing, and circuit analysis.
In economics, the second derivative is used in the study of marginal cost and marginal revenue, which are important concepts in microeconomics.
Overall, the second derivative is a fundamental concept in calculus that is used in many fields to analyze and optimize functions, systems, and processes.
When is Required Derivatives of order two
The concept of derivatives of order two, or the second derivative, is required in differential calculus when we need to analyze the curvature and concavity of a function, and to find the maximum and minimum points of a function.
We need to find the second derivative when we want to know the rate at which the rate of change of a function is changing. For example, in physics, when we want to know the acceleration of a moving object, we need to find the second derivative of its position function. Similarly, in economics, when we want to know the rate at which the marginal cost or marginal revenue is changing, we need to find the second derivative of the cost or revenue function.
The second derivative is also important in optimization problems where we need to find the maximum or minimum value of a function. The first derivative gives us the critical points of the function, where the slope of the tangent line is zero, but it does not tell us whether these points are maxima, minima or points of inflection. To determine this, we need to find the second derivative and examine its sign.
In general, the second derivative is required whenever we need to analyze the curvature or inflection points of a function or to optimize a function.
Where is Required Derivatives of order two
The concept of derivatives of order two, or the second derivative, is required in various fields where calculus is used. Some examples of where the second derivative is used include:
- Mathematics: In mathematics, the second derivative is used in the study of functions to determine the concavity and inflection points of a function. It is also used in optimization problems to find maximum and minimum points of a function.
- Physics: In physics, the second derivative is used to determine the acceleration of a moving object. It is also used in the study of motion, such as in analyzing the motion of a pendulum.
- Engineering: In engineering, the second derivative is used in the design and analysis of systems, such as in control systems and signal processing.
- Economics: In economics, the second derivative is used in the study of marginal cost and marginal revenue, which are important concepts in microeconomics.
- Chemistry: In chemistry, the second derivative is used in the analysis of spectroscopic data, such as in determining the position of spectral lines.
Overall, the second derivative is used in many fields where calculus is applied to analyze and optimize functions, systems, and processes.
How is Required Derivatives of order two
To find the second derivative, or the derivative of order two, of a function in differential calculus, we differentiate the first derivative of the function with respect to the independent variable.
Suppose we have a function f(x), then its first derivative or the derivative of order one is given by:
f'(x) = df(x)/dx
To find the second derivative, we differentiate f'(x) with respect to x, which gives:
f”(x) = d^2f(x)/dx^2
The second derivative gives information about the curvature and concavity of the function. If the second derivative is positive, the function is said to be concave up, and if the second derivative is negative, the function is said to be concave down. The points where the second derivative is zero are called inflection points, where the concavity of the function changes.
To find higher-order derivatives, we can differentiate the lower-order derivatives with respect to the independent variable. For example, the third derivative of a function is the derivative of the second derivative, which is given by:
f”'(x) = d^3f(x)/dx^3
In general, the nth derivative of a function is given by:
f^(n)(x) = d^n f(x)/dx^n
where n is a positive integer.
To apply the concept of derivatives of order two, we need to know the basic rules of differentiation, such as the power rule, product rule, quotient rule, and chain rule. We also need to know how to find critical points, inflection points, and maximum and minimum values using the first and second derivatives of a function. Additionally, we need to be familiar with different techniques for finding derivatives, such as implicit differentiation and logarithmic differentiation.
Case Study on Derivatives of order two
One example of a case study on the use of derivatives of order two in differential calculus is in the optimization of a quadratic function.
Suppose we have a quadratic function of the form:
f(x) = ax^2 + bx + c
where a, b, and c are constants. The first derivative of this function is:
f'(x) = 2ax + b
To find the maximum or minimum point of this function, we need to find the critical point where the first derivative is equal to zero. Thus, we need to solve the equation:
2ax + b = 0
which gives:
x = -b/(2a)
This is the coordinate of the vertex of the quadratic function, which is the maximum or minimum point depending on the sign of the second derivative.
To find the second derivative, we differentiate the first derivative with respect to x:
f”(x) = d/dx [2ax + b] = 2a
If the second derivative is positive, then the function is concave up, and the critical point is a minimum. If the second derivative is negative, then the function is concave down, and the critical point is a maximum. If the second derivative is zero, then the function has a point of inflection.
For example, suppose we have the quadratic function f(x) = 3x^2 – 6x + 2. The first derivative of this function is:
f'(x) = 6x – 6
Setting this derivative equal to zero and solving for x, we get:
6x – 6 = 0 x = 1
This is the coordinate of the vertex of the quadratic function. To determine whether this point is a maximum or minimum, we find the second derivative:
f”(x) = d/dx [6x – 6] = 6
Since the second derivative is positive, the function is concave up, and the critical point at x=1 is a minimum. Therefore, the minimum value of the quadratic function is:
f(1) = 3(1)^2 – 6(1) + 2 = -1
Thus, the quadratic function f(x) = 3x^2 – 6x + 2 has a minimum value of -1 at x=1. This example illustrates how the concept of derivatives of order two can be used to optimize functions and find critical points.
White paper on Derivatives of order two
Introduction:
Differential calculus is a branch of mathematics that deals with the study of rates of change and slopes of curves. Derivatives of order two, also known as the second derivative, is a fundamental concept in differential calculus. This white paper provides an in-depth explanation of the concept of derivatives of order two and its applications in various fields.
What are derivatives of order two?
A derivative of order two is the second derivative of a function. In mathematical notation, if f(x) is a function, then its second derivative is denoted by f”(x) or d²f(x)/dx². Geometrically, the second derivative measures the curvature of a curve at a given point. The sign of the second derivative determines whether the curve is concave up or concave down.
Applications of derivatives of order two:
- Optimization: The second derivative is used to find the maximum or minimum value of a function. For a function f(x), if its second derivative is positive at a point x, then the function is concave up at that point, which means the point is a local minimum. If the second derivative is negative, then the function is concave down, and the point is a local maximum.
- Physics: In physics, derivatives of order two are used to measure acceleration. The second derivative of the position function with respect to time gives the acceleration of an object at a given time.
- Economics: Derivatives of order two are used in economics to measure the elasticity of a function. The elasticity of a function measures the responsiveness of a dependent variable to changes in an independent variable.
- Engineering: In engineering, derivatives of order two are used to measure the rate of change of velocity, acceleration, and other physical quantities. They are used to design and optimize various engineering systems.
Conclusion:
Derivatives of order two are a fundamental concept in differential calculus that is widely used in various fields. The second derivative of a function provides information about the curvature and concavity of a curve. The sign of the second derivative determines whether the curve is concave up or concave down. Applications of derivatives of order two include optimization, physics, economics, and engineering. Understanding derivatives of order two is essential for analyzing and solving problems in these fields.