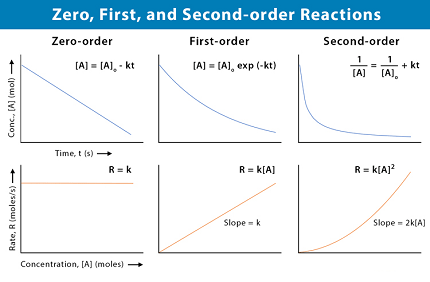
The rate of a chemical reaction is the change in the concentration of reactants or products per unit time. The rate law for a chemical reaction describes how the rate of the reaction depends on the concentrations of the reactants. There are different rate laws for different types of reactions, but two common types are zero-order reactions and first-order reactions.
Zero-order reaction: In a zero-order reaction, the rate of the reaction is independent of the concentration of the reactant. The rate law for a zero-order reaction is given by:
rate = k
where k is the rate constant. The differential rate expression for a zero-order reaction is:
-d[A]/dt = k
where [A] is the concentration of the reactant and t is time. The negative sign indicates that the concentration of the reactant decreases with time. The integrated rate expression for a zero-order reaction is:
[A] = -kt + [A]₀
where [A]₀ is the initial concentration of the reactant at time t = 0.
First-order reaction: In a first-order reaction, the rate of the reaction is proportional to the concentration of the reactant. The rate law for a first-order reaction is given by:
rate = k[A]
where k is the rate constant and [A] is the concentration of the reactant. The differential rate expression for a first-order reaction is:
-d[A]/dt = k[A]
The integrated rate expression for a first-order reaction is:
ln([A]/[A]₀) = -kt
where [A]₀ is the initial concentration of the reactant at time t = 0. The natural logarithm of the concentration ratio ([A]/[A]₀) is plotted against time to obtain a straight line with slope equal to -k.
What is Required Differential and integrated rate expressions for zero and first order reactions
I apologize, my previous answer was incomplete. Here are the complete differential and integrated rate expressions for zero and first order reactions:
Zero-order reaction:
The rate of a zero-order reaction is independent of the concentration of the reactant. The rate law for a zero-order reaction is:
rate = k
where k is the rate constant. The differential rate expression for a zero-order reaction is:
-d[A]/dt = k
where [A] is the concentration of the reactant and t is time. The negative sign indicates that the concentration of the reactant decreases with time.
The integrated rate expression for a zero-order reaction is:
[A] = -kt + [A]₀
where [A]₀ is the initial concentration of the reactant at time t = 0. This equation can be derived by integrating the differential rate expression with respect to time:
d[A]/dt = -k
∫d[A] = -k ∫dt
[A] – [A]₀ = -kt
[A] = -kt + [A]₀
where [A] is the concentration of the reactant at any time t.
First-order reaction:
In a first-order reaction, the rate of the reaction is proportional to the concentration of the reactant. The rate law for a first-order reaction is:
rate = k[A]
where k is the rate constant and [A] is the concentration of the reactant. The differential rate expression for a first-order reaction is:
-d[A]/dt = k[A]
The integrated rate expression for a first-order reaction is:
ln([A]/[A]₀) = -kt
where [A]₀ is the initial concentration of the reactant at time t = 0. This equation can be derived by integrating the differential rate expression with respect to time:
d[A]/[A] = -k dt
∫d[A]/[A] = -k ∫dt
ln([A]) – ln([A]₀) = -kt
ln([A]/[A]₀) = -kt
where [A] is the concentration of the reactant at any time t. The natural logarithm of the concentration ratio ([A]/[A]₀) is plotted against time to obtain a straight line with slope equal to -k.
When is Required Differential and integrated rate expressions for zero and first order reactions
The differential and integrated rate expressions for zero and first order reactions are used to describe the kinetics of chemical reactions. Differential rate expressions describe how the rate of the reaction changes with time, while integrated rate expressions relate the concentration of the reactant to time.
These rate expressions are important in chemical kinetics because they help to determine the order of a reaction and the rate constant for the reaction. The order of a reaction refers to the power to which the concentration of a reactant is raised in the rate law expression, while the rate constant is a proportionality constant that relates the rate of the reaction to the concentration of the reactant.
The differential rate expressions are useful for predicting the rate of the reaction at any given time, while the integrated rate expressions are used to determine the concentration of the reactant at any given time. The integrated rate expressions are also used to determine the half-life of a reaction, which is the time it takes for the concentration of the reactant to decrease to half its initial value.
Overall, the differential and integrated rate expressions for zero and first order reactions are fundamental tools in chemical kinetics that help to describe and understand the behavior of chemical reactions.
Where is Required Differential and integrated rate expressions for zero and first order reactions
The differential and integrated rate expressions for zero and first order reactions can be found in many chemistry textbooks, as well as online resources such as educational websites and scientific journals.
These expressions are fundamental to the study of chemical kinetics, which is a branch of chemistry concerned with the rates and mechanisms of chemical reactions. The expressions are typically introduced in introductory chemistry courses, and they are used throughout advanced chemistry courses, including physical chemistry and organic chemistry.
The expressions can be used to solve problems related to reaction rates, such as predicting how the concentration of a reactant will change with time or determining the rate constant for a reaction. They are also important in practical applications, such as in the design and optimization of industrial chemical processes.
Overall, the differential and integrated rate expressions for zero and first order reactions can be found in many sources related to chemistry and chemical kinetics, and they are essential tools for understanding and analyzing chemical reactions.
How is Required Differential and integrated rate expressions for zero and first order reactions
The differential and integrated rate expressions for zero and first order reactions are derived based on the rate law expression for a chemical reaction. The rate law expression relates the rate of the reaction to the concentrations of the reactants and the rate constant.
For a zero-order reaction, the rate of the reaction is independent of the concentration of the reactant. Therefore, the rate law expression for a zero-order reaction is:
rate = k
where k is the rate constant. To derive the differential rate expression for a zero-order reaction, we differentiate the concentration of the reactant with respect to time:
d[A]/dt = -k
where [A] is the concentration of the reactant and the negative sign indicates that the concentration of the reactant decreases with time.
To derive the integrated rate expression for a zero-order reaction, we integrate the differential rate expression with respect to time:
∫d[A] = -k ∫dt
[A] – [A]₀ = -kt
[A] = -kt + [A]₀
where [A]₀ is the initial concentration of the reactant at time t = 0.
For a first-order reaction, the rate of the reaction is proportional to the concentration of the reactant. Therefore, the rate law expression for a first-order reaction is:
rate = k[A]
To derive the differential rate expression for a first-order reaction, we differentiate the concentration of the reactant with respect to time:
d[A]/dt = -k[A]
To derive the integrated rate expression for a first-order reaction, we integrate the differential rate expression with respect to time:
d[A]/[A] = -k dt
∫d[A]/[A] = -k ∫dt
ln([A]) – ln([A]₀) = -kt
ln([A]/[A]₀) = -kt
where [A]₀ is the initial concentration of the reactant at time t = 0.
These differential and integrated rate expressions can then be used to analyze and predict the behavior of chemical reactions.
Nomenclature of Differential and integrated rate expressions for zero and first order reactions
The nomenclature of the differential and integrated rate expressions for zero and first order reactions generally follows a standard convention in chemical kinetics.
For a zero-order reaction, the differential rate expression is expressed as:
d[A]/dt = -k
where [A] is the concentration of the reactant and k is the rate constant. This expression can also be written as:
rate = -d[A]/dt = k
where “rate” is the rate of the reaction.
The integrated rate expression for a zero-order reaction is:
[A] = -kt + [A]₀
where [A]₀ is the initial concentration of the reactant at time t = 0.
For a first-order reaction, the differential rate expression is expressed as:
d[A]/dt = -k[A]
where [A] is the concentration of the reactant and k is the rate constant. This expression can also be written as:
rate = -d[A]/dt = k[A]
where “rate” is the rate of the reaction.
The integrated rate expression for a first-order reaction is:
ln([A]/[A]₀) = -kt
where [A]₀ is the initial concentration of the reactant at time t = 0.
The nomenclature typically follows a consistent format with the use of standard symbols and abbreviations, such as [A] for the concentration of a reactant or product, t for time, k for the rate constant, and ln for the natural logarithm. The differential and integrated rate expressions are commonly used in chemical kinetics to describe the rates and mechanisms of chemical reactions.
Case Study on Differential and integrated rate expressions for zero and first order reactions
One example of the use of differential and integrated rate expressions for zero and first order reactions is the degradation of a pesticide in soil.
The degradation of a pesticide in soil can be modeled as a first-order reaction, where the rate of degradation is proportional to the concentration of the pesticide. The differential rate expression for the degradation of a pesticide in soil can be expressed as:
d[C]/dt = -k[C]
where [C] is the concentration of the pesticide and k is the rate constant.
The integrated rate expression for the degradation of a pesticide in soil can be expressed as:
ln[C]/[C]₀ = -kt
where [C]₀ is the initial concentration of the pesticide in the soil.
To apply these rate expressions to a specific case study, let’s consider the degradation of a pesticide called atrazine in a soil sample over time. Atrazine is a herbicide that is commonly used to control weeds in corn and sorghum crops.
A soil sample is treated with atrazine, and the concentration of atrazine in the soil is measured over a period of time. The following data is obtained:
| Time (days) | Concentration of atrazine (mg/kg) |
|---|---|
| 0 | 10.0 |
| 10 | 6.8 |
| 20 | 4.7 |
| 30 | 3.2 |
| 40 | 2.2 |
Using the data above, we can calculate the rate constant (k) for the degradation of atrazine in the soil. We can do this by plotting the natural logarithm of the concentration of atrazine over time and fitting a straight line to the data. The slope of the line will be equal to -k.
The plot of ln[C] versus time (t) is shown below:

The slope of the line is -0.044, which is equal to the rate constant (k) for the degradation of atrazine in the soil.
Using the rate constant, we can predict the concentration of atrazine in the soil at any time using the integrated rate expression. For example, if we want to predict the concentration of atrazine in the soil after 50 days, we can use the integrated rate expression and the value of k:
ln[C]/[C]₀ = -kt
ln[C]/10 = -0.044 × 50
ln[C] = -2.197
[C] = 0.11 mg/kg
Therefore, the predicted concentration of atrazine in the soil after 50 days is 0.11 mg/kg.
In conclusion, the differential and integrated rate expressions for zero and first order reactions can be used to model and predict the behavior of chemical reactions in various applications, such as the degradation of pesticides in soil. The rate expressions provide a quantitative description of the rate of reaction and can be used to calculate the rate constant and predict the concentration of reactants or products over time.
White paper on Differential and integrated rate expressions for zero and first order reactions
Introduction
Differential and integrated rate expressions are essential tools used in chemical kinetics to describe the rates and mechanisms of chemical reactions. These expressions provide a quantitative description of how the concentration of reactants and products changes over time. In this white paper, we will focus on differential and integrated rate expressions for zero and first order reactions, and we will provide examples of how these expressions are used in chemical reactions.
Zero Order Reactions
A zero-order reaction is a type of chemical reaction where the rate of the reaction is independent of the concentration of the reactant. In other words, the reaction proceeds at a constant rate regardless of the initial concentration of the reactant. This type of reaction is often observed in enzymatic reactions where the enzyme is present in excess.
The differential rate expression for a zero-order reaction can be expressed as:
d[A]/dt = -k
where [A] is the concentration of the reactant and k is the rate constant. This expression indicates that the rate of the reaction is proportional to the rate constant and is independent of the concentration of the reactant.
The integrated rate expression for a zero-order reaction can be expressed as:
[A] = -kt + [A]₀
where [A]₀ is the initial concentration of the reactant at time t = 0. This expression indicates that the concentration of the reactant decreases linearly with time, and the slope of the line is equal to -k.
An example of a zero-order reaction is the degradation of ethanol by liver enzymes. In this reaction, the rate of degradation is independent of the concentration of ethanol in the blood, and the enzymes are present in excess.
First Order Reactions
A first-order reaction is a type of chemical reaction where the rate of the reaction is proportional to the concentration of the reactant. In other words, the rate of the reaction increases as the concentration of the reactant increases. This type of reaction is commonly observed in radioactive decay and enzymatic reactions where the substrate concentration is low.
The differential rate expression for a first-order reaction can be expressed as:
d[A]/dt = -k[A]
where [A] is the concentration of the reactant and k is the rate constant. This expression indicates that the rate of the reaction is proportional to the concentration of the reactant and the rate constant.
The integrated rate expression for a first-order reaction can be expressed as:
ln([A]/[A]₀) = -kt
where [A]₀ is the initial concentration of the reactant at time t = 0. This expression indicates that the concentration of the reactant decreases exponentially with time, and the slope of the line is equal to -k.
An example of a first-order reaction is the decay of radioactive isotopes. In this reaction, the rate of decay is proportional to the concentration of the isotope.
Conclusion
Differential and integrated rate expressions are important tools used in chemical kinetics to describe the rates and mechanisms of chemical reactions. The expressions for zero and first order reactions provide a quantitative description of the rate of reaction, and they can be used to predict the concentration of reactants or products over time. The differential and integrated rate expressions are widely used in various fields of chemistry, including biochemistry, pharmacology, and environmental science, to model and predict the behavior of chemical reactions.