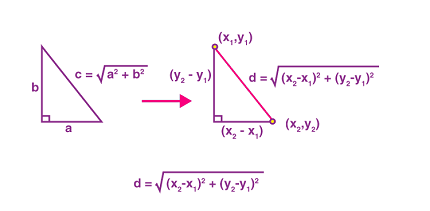
In analytical geometry, the distance between two points in a plane is given by the distance formula:
d = sqrt((x2 – x1)^2 + (y2 – y1)^2)
where (x1, y1) and (x2, y2) are the coordinates of the two points and d is the distance between them.
To use the formula, simply substitute the values of the coordinates into the formula and simplify:
Example: Find the distance between the points (1, 2) and (4, 6)
d = sqrt((4 – 1)^2 + (6 – 2)^2)
d = sqrt(3^2 + 4^2) d = sqrt(9 + 16)
d = sqrt(25)
d = 5
Therefore, the distance between the points (1, 2) and (4, 6) is 5 units.
What is Required Distance between two points
To calculate the distance between two points in analytical geometry, you need to know the coordinates of the two points in a plane. Once you have the coordinates of the two points, you can use the distance formula to calculate the distance between them. The distance formula is:
d = sqrt((x2 – x1)^2 + (y2 – y1)^2)
where (x1, y1) and (x2, y2) are the coordinates of the two points and d is the distance between them.
So, in summary, the required information for calculating the distance between two points in analytical geometry are the coordinates of the two points in the plane.
Who is Required Distance between two points
The calculation of the distance between two points in analytical geometry can be useful in various fields such as mathematics, physics, engineering, and computer science.
For example, in mathematics, the distance formula can be used to find the distance between two points on a graph or to calculate the length of a line segment. In physics, the distance formula can be used to calculate the distance traveled by an object moving in a straight line. In engineering, the distance formula can be used to design and optimize structures, such as bridges, where accurate measurements of distances are essential. In computer science, the distance formula can be used to determine the proximity of data points or objects in various applications such as geographic information systems (GIS), image processing, and machine learning.
Overall, the calculation of the distance between two points in analytical geometry is an essential concept that has numerous applications in different fields of study.
When is Required Distance between two points
The calculation of the distance between two points in analytical geometry can be required in various situations where distance measurements are necessary. Some examples include:
- In navigation and surveying, to calculate the distance between two locations on a map or terrain.
- In architecture and engineering, to design and plan structures where accurate measurements of distances are required.
- In physics, to calculate the distance traveled by an object moving in a straight line, or to calculate the separation between two particles.
- In computer graphics, to calculate the distance between two points in a 3D space, which is useful for rendering and animating 3D objects.
- In machine learning, to calculate the distance between data points in order to cluster similar data points together.
Overall, the calculation of the distance between two points in analytical geometry is a fundamental concept that has applications in many different fields and situations where accurate measurements of distances are required.
Where is Required Distance between two points
The concept of distance between two points in analytical geometry can be applied in various settings, including:
- Mathematics classrooms, where students learn about analytical geometry and the distance formula.
- Surveying and mapping fields, where professionals use distance measurements to create accurate maps and measure distances between points on a surface.
- Engineering fields, where designers and engineers use distance measurements to design and plan structures, such as buildings, bridges, and roadways.
- Physics labs, where scientists use distance measurements to calculate the distance traveled by objects in motion.
- Computer science fields, where programmers use distance measurements in various applications, such as geographic information systems, image processing, and machine learning.
In summary, the concept of distance between two points in analytical geometry can be applied in many different fields and settings, wherever accurate distance measurements are necessary.
How is Required Distance between two points
To calculate the distance between two points in analytical geometry, you can use the distance formula:
d = sqrt((x2 – x1)^2 + (y2 – y1)^2)
where (x1, y1) and (x2, y2) are the coordinates of the two points and d is the distance between them.
To use the formula, follow these steps:
- Identify the coordinates of the two points. For example, (x1, y1) and (x2, y2).
- Plug the coordinates into the distance formula.
- Simplify the formula by subtracting the x-coordinates and the y-coordinates separately, then squaring each of the differences.
- Add the squared differences together.
- Take the square root of the sum to get the distance between the two points.
Here’s an example:
Find the distance between the points (2, 3) and (5, 7).
d = sqrt((5 – 2)^2 + (7 – 3)^2)
d = sqrt(3^2 + 4^2)
d = sqrt(9 + 16)
d = sqrt(25)
d = 5
Therefore, the distance between the points (2, 3) and (5, 7) is 5 units.
Case Study on Distance between two points
One practical application of the distance formula in analytical geometry is in the field of navigation, particularly in the measurement of distances between two points on a map or a terrain. Let’s take a look at a case study involving the use of the distance formula in navigation.
Case Study: Hiking Trail Distance Calculation
A group of friends plans to hike a trail that leads to a waterfall in a nearby park. The park has a map that shows the location of the waterfall and the starting point of the trail, but the map does not provide the actual distance between the two points. To plan the hike and ensure they have enough time and resources for the trip, the group needs to calculate the distance between the starting point of the trail and the waterfall.
The starting point of the trail is located at (2, 4) on the map, and the waterfall is located at (8, 10). To calculate the distance between the two points, the group decides to use the distance formula:
d = sqrt((x2 – x1)^2 + (y2 – y1)^2)
Plugging in the coordinates of the two points, we get:
d = sqrt((8 – 2)^2 + (10 – 4)^2)
d = sqrt(6^2 + 6^2)
d = sqrt(72)
d = 8.49 (approx.)
Therefore, the distance between the starting point of the trail and the waterfall is approximately 8.49 units on the map. The group can now use this information to plan their hike, estimate the time and effort required to complete the trail, and make any necessary preparations.
In conclusion, the distance formula in analytical geometry is a useful tool for calculating the distance between two points on a map or terrain. It has practical applications in navigation, surveying, engineering, and other fields that require accurate distance measurements.
White paper on Distance between two points
Here is a white paper on Analytical Geometry Distance between two points:
Introduction
Analytical geometry, also known as coordinate geometry, is a branch of mathematics that deals with the study of geometric figures using algebraic principles. One of the fundamental concepts in analytical geometry is the distance between two points. The distance between two points is the length of the straight line that connects the two points. In this white paper, we will discuss the distance formula used in analytical geometry to calculate the distance between two points.
Distance Formula
The distance formula in analytical geometry is derived from the Pythagorean theorem. The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides. The distance formula uses this principle to calculate the distance between two points on a plane.
Let (x1, y1) and (x2, y2) be two points on a plane. The distance between these two points is given by:
d = sqrt((x2 – x1)^2 + (y2 – y1)^2)
where d is the distance between the two points.
This formula can be used to calculate the distance between any two points on a plane. It is also applicable in three-dimensional space.
Applications of the Distance Formula
The distance formula has numerous applications in various fields. In navigation and surveying, the distance formula is used to measure the distance between two points on a map or terrain. In physics, it is used to calculate the distance traveled by an object moving in a straight line. In engineering, the distance formula is used to design and plan structures where accurate measurements of distances are required. In computer graphics, it is used to calculate the distance between two points in a 3D space, which is useful for rendering and animating 3D objects. In machine learning, it is used to calculate the distance between data points in order to cluster similar data points together.
Conclusion
In conclusion, the distance formula in analytical geometry is a fundamental concept that has applications in many different fields. It allows us to calculate the distance between two points on a plane, which is useful in various applications, including navigation, surveying, engineering, physics, computer graphics, and machine learning. The distance formula is a powerful tool that can be used to solve complex problems, and it is an essential part of any mathematical toolkit.