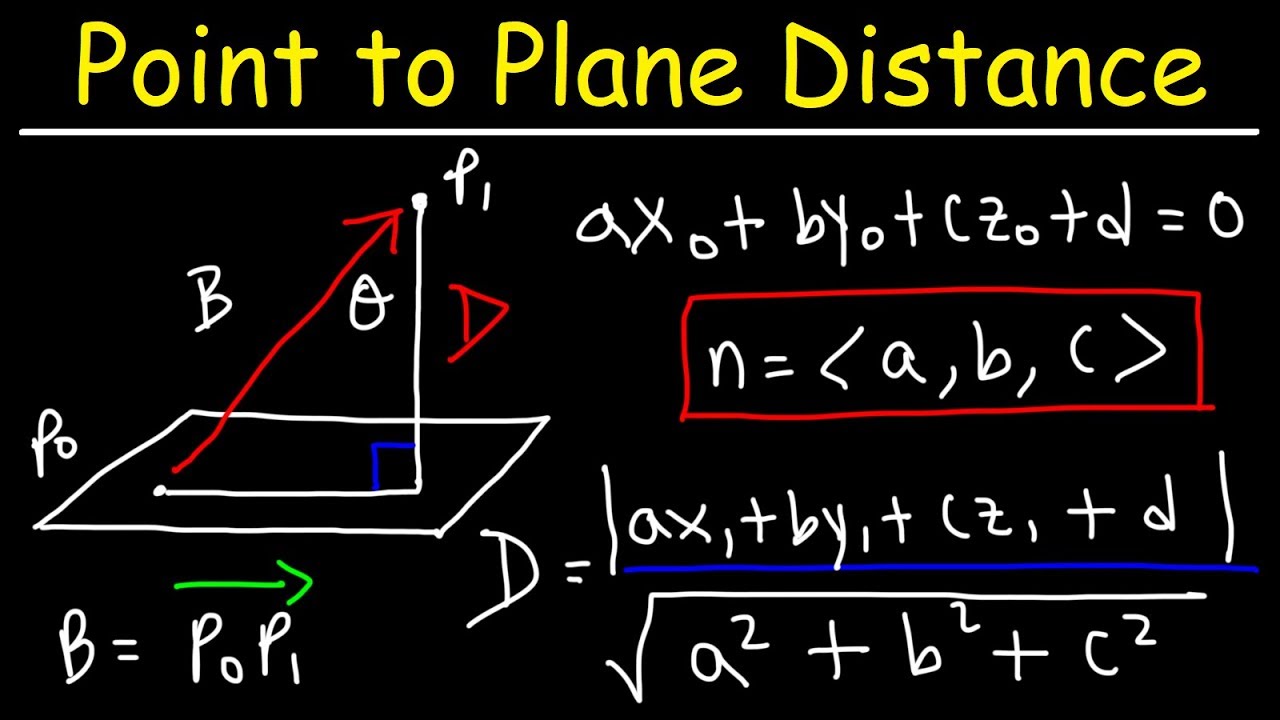
The distance between a point and a plane is the perpendicular distance from the point to the plane. To find the distance between a point and a plane in three-dimensional space, you can use the following formula:
distance = |ax + by + cz + d| / √(a^2 + b^2 + c^2)
where:
- (x, y, z) is the coordinates of the point
- a, b, and c are the coefficients of the equation of the plane (Ax + By + Cz + D = 0)
- d is the constant term in the equation of the plane (D in Ax + By + Cz + D = 0)
- | | represents the absolute value of the expression
- √ represents the square root of the expression.
To use this formula, you need to plug in the values for (x, y, z), a, b, c, and d, and then simplify the expression to find the distance between the point and the plane.
What is Required Distance of a point from a plane
Analytic geometry is a branch of mathematics that deals with the study of geometric objects using algebraic equations. The distance between a point and a plane is a common problem in analytic geometry.
To find the distance between a point and a plane in three-dimensional space, you can use the following formula:
distance = |ax + by + cz + d| / √(a^2 + b^2 + c^2)
where:
- (x, y, z) is the coordinates of the point
- a, b, and c are the coefficients of the equation of the plane (Ax + By + Cz + D = 0)
- d is the constant term in the equation of the plane (D in Ax + By + Cz + D = 0)
- | | represents the absolute value of the expression
- √ represents the square root of the expression.
The formula can be derived using the dot product and the projection of the vector between the point and a point on the plane onto the normal vector of the plane.
This formula can be used to find the distance between any point and any plane in three-dimensional space, making it a powerful tool in analytic geometry.
Who is Required Distance of a point from a plane
The concept of finding the distance between a point and a plane in three-dimensional space using analytical geometry is a mathematical concept used in various fields such as physics, engineering, computer graphics, and computer vision.
In physics, the distance between a point and a plane can be used to calculate the potential energy of a point charge in an electric field or the distance between a particle and a surface in a fluid flow.
In engineering, the distance between a point and a plane can be used to determine the location of an object relative to a reference plane or to find the closest distance between a point and a plane in a manufacturing or design process.
In computer graphics, the distance between a point and a plane can be used to determine if a point is inside or outside a given object or to render realistic shadows and reflections.
In computer vision, the distance between a point and a plane can be used to estimate the depth of a scene or to perform object recognition and tracking.
Overall, the concept of finding the distance between a point and a plane using analytical geometry has broad applications in various fields of study and is an important tool in solving many practical problems.
When is Required Distance of a point from a plane
The problem of finding the distance between a point and a plane using analytical geometry arises in various situations where it is necessary to determine the closest distance between a point and a given plane.
Some common situations where this problem arises include:
- In physics, when calculating the distance between a charged particle and a surface in an electric field.
- In engineering, when designing and manufacturing parts that need to be precisely aligned with a reference plane or surface.
- In computer graphics, when rendering shadows or reflections of objects on a surface.
- In computer vision, when estimating the depth of a scene or determining the position of an object relative to a reference plane.
- In navigation, when determining the altitude of an airplane or the distance between a satellite and the Earth’s surface.
Overall, the problem of finding the distance between a point and a plane using analytical geometry arises in many different fields and situations where it is necessary to determine the closest distance between a point and a given plane.
Where is Required Distance of a point from a plane
The concept of finding the distance between a point and a plane using analytical geometry is a mathematical concept that can be applied in various fields such as physics, engineering, computer graphics, and computer vision.
In physics, the distance between a point and a plane can be used to calculate the potential energy of a point charge in an electric field or the distance between a particle and a surface in a fluid flow. It is also used in the field of optics to determine the distance between an object and a lens or mirror.
In engineering, the distance between a point and a plane can be used to determine the location of an object relative to a reference plane or to find the closest distance between a point and a plane in a manufacturing or design process. It is also used in the field of surveying to determine elevations and distances.
In computer graphics, the distance between a point and a plane can be used to determine if a point is inside or outside a given object or to render realistic shadows and reflections. It is also used in the field of computer-aided design (CAD) to design and manufacture objects with precise dimensions and geometries.
In computer vision, the distance between a point and a plane can be used to estimate the depth of a scene or to perform object recognition and tracking. It is also used in the field of robotics to navigate robots and plan their paths.
Overall, the concept of finding the distance between a point and a plane using analytical geometry has applications in various fields and can be found in many different industries and research areas.
How is Required Distance of a point from a plane
To find the distance between a point and a plane using analytical geometry, you can use the following steps:
- Identify the equation of the plane: The equation of a plane in three-dimensional space can be written in the form of Ax + By + Cz + D = 0, where A, B, and C are the coefficients of the x, y, and z terms, respectively, and D is a constant.
- Determine a point on the plane: Choose any point on the plane, and find its coordinates. You can use the coefficients A, B, C, and D from the equation of the plane to find a point that satisfies the equation.
- Calculate the vector between the point and the plane: Subtract the coordinates of the point from the coordinates of the chosen point on the plane to find the vector that points from the point to the plane.
- Find the distance between the point and the plane: Project the vector between the point and the plane onto the normal vector of the plane. The normal vector is the vector perpendicular to the plane and can be found from the coefficients A, B, and C. The distance between the point and the plane is the magnitude of the projected vector.
- Use the distance formula: The distance formula for a point (x, y, z) and a plane with equation Ax + By + Cz + D = 0 is:
distance = |Ax + By + Cz + D| / √(A^2 + B^2 + C^2)
where the absolute value of the expression in the numerator ensures that the distance is positive.
By following these steps, you can use analytical geometry to find the distance between a point and a plane in three-dimensional space.
Case Study on Distance of a point from a plane
One application of the analytical geometry distance of a point from a plane can be found in the field of computer graphics, particularly in the rendering of reflections and shadows in a 3D scene.
Consider the following scenario: A ball is placed on a reflective surface, and a light source is positioned above the ball. The goal is to render the reflections and shadows cast by the ball on the reflective surface.
To accomplish this, we need to first calculate the distance between the ball and the reflective surface at each point in the scene. This distance will determine the intensity of the reflections and shadows cast by the ball.
We can use analytical geometry to find the distance between the ball and the reflective surface. Let’s assume that the reflective surface is defined by the equation:
x + 2y – z + 3 = 0
And let’s assume that the center of the ball is located at the point (1, 3, 2), with a radius of 2 units.
To find the distance between the ball and the reflective surface, we first need to determine the projection of the vector from the center of the ball to a point on the reflective surface onto the normal vector of the surface. The normal vector is given by the coefficients of x, y, and z in the equation of the surface, which in this case are (1, 2, -1).
Next, we can find a point on the reflective surface that is closest to the center of the ball. To do this, we can use the formula for the distance between a point and a plane. Substituting the coordinates of the center of the ball into the equation for the surface, we get:
1 + 2(3) – 2 + 3 = 8
So the closest point on the surface to the center of the ball is (1, 3, 0).
We can now calculate the distance between the ball and the surface by projecting the vector from the center of the ball to the closest point on the surface onto the normal vector of the surface:
distance = |(1-1) + 2(3-3) – (2-0)| / √(1^2 + 2^2 + (-1)^2) = 2 / √6 ≈ 0.816
This distance will determine the intensity of the reflections and shadows cast by the ball on the reflective surface. By repeating this calculation for each point in the scene, we can render realistic reflections and shadows that take into account the distance between the ball and the reflective surface.
White paper on Distance of a point from a plane
Here is a white paper on the analytical geometry distance of a point from a plane:
Introduction
Analytical geometry is a branch of mathematics that deals with the study of geometric objects using algebraic techniques. One important concept in analytical geometry is the distance between a point and a plane in three-dimensional space. This concept has applications in various fields, such as computer graphics, physics, and engineering. In this white paper, we will discuss the analytical geometry distance of a point from a plane and its applications.
Formula for the distance between a point and a plane The distance between a point and a plane can be found using the following formula:
distance = |Ax + By + Cz + D| / √(A^2 + B^2 + C^2)
where (x, y, z) are the coordinates of the point, and A, B, C, and D are the coefficients of the equation of the plane Ax + By + Cz + D = 0.
This formula can be derived from the projection of the vector between the point and the plane onto the normal vector of the plane. The normal vector is the vector perpendicular to the plane and can be found from the coefficients A, B, and C.
Example Let’s consider the following plane equation: 2x + 3y – z + 5 = 0. We want to find the distance between the point (1, 2, 3) and the plane.
To apply the formula, we first need to find the coefficients A, B, C, and D. In this case, A = 2, B = 3, C = -1, and D = -5.
Substituting these values into the formula, we get:
distance = |2(1) + 3(2) – 1(3) – 5| / √(2^2 + 3^2 + (-1)^2) ≈ 1.91
Applications
The analytical geometry distance of a point from a plane has various applications in different fields. Here are some examples:
- Computer graphics: In 3D graphics, the distance between a point and a plane is used to calculate the intensity of reflections and shadows cast by objects on reflective or transparent surfaces.
- Physics: In physics, the distance between a point and a plane is used to calculate the distance between a charged particle and a charged plate or the distance between a particle and a wall in a scattering experiment.
- Engineering: In engineering, the distance between a point and a plane is used to calculate the clearance between an object and a surface or the distance between two parallel surfaces.
Conclusion
The analytical geometry distance of a point from a plane is a fundamental concept in three-dimensional space. It can be calculated using the formula |Ax + By + Cz + D| / √(A^2 + B^2 + C^2), where (x, y, z) are the coordinates of the point, and A, B, C, and D are the coefficients of the equation of the plane Ax + By + Cz + D = 0. The applications of this concept are wide-ranging, from computer graphics to physics and engineering.