Vrindawan Coaching Center

Domain and codomain of relations

domain and codomain of relations, JEE Mathematics, , , , , , ,
File:Domain, Range, Codomain.svg - Wikimedia Commons

In mathematics, a relation is a set of ordered pairs that relate elements of two sets. The domain and codomain are important concepts when it comes to understanding relations.

The domain of a relation is the set of all first elements of the ordered pairs in the relation. In other words, it is the set of all elements that appear in the first position of the ordered pairs.

The codomain of a relation is the set of all possible second elements of the ordered pairs in the relation. In other words, it is the set of all elements that could potentially appear in the second position of the ordered pairs.

For example, consider the relation R = {(1,2), (3,4), (1,3)}. The domain of R is {1, 3}, since those are the first elements of the ordered pairs. The codomain of R is {2, 3, 4}, since those are all possible second elements of the ordered pairs.

It is important to note that not all elements in the codomain need to be paired with elements in the domain. In the example above, 2 and 4 are not paired with any element in the domain. However, all elements in the domain must have at least one corresponding element in the codomain.

Binary relation

In mathematics, a binary relation associates elements of one set, called the domain, with elements of another set, called the codomain. A binary relation over sets X and Y is a new set of ordered pairs (x, y) consisting of elements x in X and y in Y. It is a generalization of the more widely understood idea of a unary function. It encodes the common concept of relation: an element x is related to an element y, if and only if the pair (x, y) belongs to the set of ordered pairs that defines the binary relation. A binary relation is the most studied special case n = 2 of an n-ary relation over sets X1, …, Xn, which is a subset of the Cartesian product 1×⋯×{\displaystyle X_{1}\times \cdots \times X_{n}.}

An example of a binary relation is the “divides” relation over the set of prime numbers \mathbb {P}  and the set of integers \mathbb {Z} , in which each prime p is related to each integer z that is a multiple of p, but not to an integer that is not a multiple of p. In this relation, for instance, the prime number 2 is related to numbers such as −4, 0, 6, 10, but not to 1 or 9, just as the prime number 3 is related to 0, 6, and 9, but not to 4 or 13.

Binary relations are used in many branches of mathematics to model a wide variety of concepts. These include, among others:

A function may be defined as a special kind of binary relation. Binary relations are also heavily used in computer science.

A binary relation over sets X and Y is an element of the power set of {\displaystyle X\times Y.} Since the latter set is ordered by inclusion (⊆), each relation has a place in the lattice of subsets of {\displaystyle X\times Y.} A binary relation is called a homogeneous relation when X = Y. A binary relation is also called a heterogeneous relation when it is not necessary that X = Y.

Since relations are sets, they can be manipulated using set operations, including union, intersection, and complementation, and satisfying the laws of an algebra of sets. Beyond that, operations like the converse of a relation and the composition of relations are available, satisfying the laws of a calculus of relations, for which there are textbooks by Ernst Schröder, Clarence Lewis, and Gunther Schmidt. A deeper analysis of relations involves decomposing them into subsets called concepts, and placing them in a complete lattice.

In some systems of axiomatic set theory, relations are extended to classes, which are generalizations of sets. This extension is needed for, among other things, modeling the concepts of “is an element of” or “is a subset of” in set theory, without running into logical inconsistencies such as Russell’s paradox.

The terms correspondence, dyadic relation and two-place relation are synonyms for binary relation, though some authors use the term “binary relation” for any subset of a Cartesian product X\times Y without reference to X and Y, and reserve the term “correspondence” for a binary relation with reference to X and Y.

Domain of a function

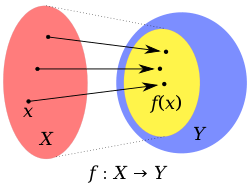
In mathematics, the domain of a function is the set of inputs accepted by the function. It is sometimes denoted by {\displaystyle \operatorname {dom} (f)} or {\displaystyle \operatorname {dom} f}, where f is the function.

More precisely, given a function f\colon X\to Y, the domain of f is X. Note that in modern mathematical language, the domain is part of the definition of a function rather than a property of it.

In the special case that X and Y are both subsets of \mathbb {R} , the function f can be graphed in the Cartesian coordinate system. In this case, the domain is represented on the x-axis of the graph, as the projection of the graph of the function onto the x-axis.

For a function f\colon X\to Y, the set Y is called the codomain, and the set of values attained by the function (which is a subset of Y) is called its range or image.

Any function can be restricted to a subset of its domain. The restriction of f \colon X \to Y to A, where A\subseteq X, is written as {\displaystyle \left.f\right|_{A}\colon A\to Y}.

When is Required domain and codomain of relations

It is always necessary to specify the domain and codomain of a relation, as they provide important information about the nature of the relation.

The domain and codomain help us determine whether a relation is well-defined, which means that every element in the domain is related to an element in the codomain, and that each element in the domain is related to at most one element in the codomain.

In addition, the domain and codomain help us understand the range of a relation, which is the set of all second elements of the ordered pairs in the relation. The range is a subset of the codomain, and it represents all the possible outputs of the relation for any input in the domain.

For example, if we consider the relation R = {(x, x^2) | x ∈ R}, where R is the set of real numbers, then the domain is R and the codomain is also R. The range, however, is the set of all non-negative real numbers, since for any real number x, x^2 is always non-negative.

In summary, the domain and codomain are necessary to define a relation and to ensure that it is well-defined. They also help us understand the possible inputs and outputs of the relation, and they provide important information about its range.

Where is Required domain and codomain of relations

The concept of domain and codomain is used in many areas of mathematics, including set theory, algebra, analysis, topology, and computer science.

In set theory, relations are used to describe how elements of different sets are related to each other. The domain and codomain of a relation are used to specify the sets from which the elements come and to which they go.

In algebra, relations are used to describe operations and functions between sets of elements. The domain and codomain of a function are used to specify the inputs and outputs of the function, and to ensure that the function is well-defined.

In analysis, relations are used to describe the behavior of continuous functions and their limits. The domain and codomain of a function are used to specify the set of values over which the function is defined, and the set of values to which it can be extended.

In topology, relations are used to describe the topological structure of spaces and their properties. The domain and codomain of a relation are used to specify the sets of points and the types of connections between them.

In computer science, relations are used to model data structures, algorithms, and programming languages. The domain and codomain of a relation are used to specify the types of data that can be input and output by a program or an algorithm.

Overall, the concept of domain and codomain is a fundamental tool in mathematics and is used in many different areas of the field.

How is Required domain and codomain of relations

The domain and codomain of a relation are required to properly define and understand the relation. Here is how the domain and codomain are used in defining relations:

  1. To specify the sets of elements: The domain and codomain specify the sets of elements that are related by the relation. The domain is the set of all first elements of the ordered pairs in the relation, while the codomain is the set of all possible second elements of the ordered pairs.
  2. To ensure the relation is well-defined: A relation is well-defined if every element in the domain is related to an element in the codomain, and each element in the domain is related to at most one element in the codomain. The domain and codomain help to ensure that the relation is well-defined.
  3. To determine the range: The range of a relation is the set of all second elements of the ordered pairs in the relation. The range is a subset of the codomain and represents all the possible outputs of the relation for any input in the domain.
  4. To determine the type of relation: The domain and codomain can be used to determine the type of relation. For example, if the domain and codomain are the same set, then the relation is called an endorelation. If the domain and codomain are different sets, then the relation is called a binary relation.

Overall, the domain and codomain of a relation are essential concepts that allow us to define and understand relations in mathematics. They help to ensure that the relation is well-defined, and they provide information about the range of the relation and the type of relation.

Case Study on domain and codomain of relations

Here is a case study that illustrates the importance of domain and codomain in understanding relations:

Case Study: A relation between students and their grades

Consider a relation between students and their grades in a class. Let S be the set of all students in the class, and let G be the set of all possible grades that a student can receive (e.g., A, B, C, D, or F).

The relation R can be defined as follows: R = {(s, g) | s is a student in the class and received grade g in the class}.

In this case, the domain of the relation is the set of all students in the class, and the codomain is the set of all possible grades that a student can receive. The domain and codomain are important for understanding the nature of this relation.

If the domain and codomain are not properly defined, it can lead to ambiguity and confusion. For example, if the domain is not specified, we cannot be sure which students are included in the relation. If the codomain is not specified, we cannot be sure which grades are possible.

Moreover, the domain and codomain help us to ensure that the relation is well-defined. For example, we can use the domain and codomain to check whether there are any students who did not receive a grade or any grades that were not received by any student.

Finally, the domain and codomain help us to understand the range of the relation. In this case, the range is the set of all grades that were received by at least one student in the class. By specifying the domain and codomain, we can determine the range and gain insights into the performance of the class as a whole.

In conclusion, the domain and codomain of a relation are essential concepts that allow us to define and understand relations in a variety of contexts. They help us to ensure that the relation is well-defined, to determine the range of the relation, and to gain insights into the nature of the relation itself.

White paper on domain and codomain of relations

Here is a white paper that provides a detailed explanation of the domain and codomain of relations in mathematics:

Introduction:

Relations are an important concept in mathematics, and they are used to describe how elements of different sets are related to each other. A relation is a set of ordered pairs, where each ordered pair consists of two elements, one from each of two sets. The domain and codomain of a relation are used to specify the sets from which the elements come and to which they go. This white paper provides a detailed explanation of the domain and codomain of relations.

Definition of Domain and Codomain:

The domain of a relation is the set of all first elements of the ordered pairs in the relation. In other words, it is the set of all elements that are input into the relation. The codomain of a relation is the set of all possible second elements of the ordered pairs. In other words, it is the set of all possible outputs of the relation for any input in the domain.

Example:

Consider the relation R = {(1, a), (2, b), (3, c), (4, d)}. In this relation, the domain is {1, 2, 3, 4}, and the codomain is {a, b, c, d}. The domain specifies the set of inputs, which are the first elements of the ordered pairs in the relation. The codomain specifies the set of outputs, which are the possible second elements of the ordered pairs.

Importance of Domain and Codomain:

The domain and codomain are important for several reasons:

  1. Well-Definedness: A relation is well-defined if every element in the domain is related to an element in the codomain, and each element in the domain is related to at most one element in the codomain. The domain and codomain help to ensure that the relation is well-defined.
  2. Range: The range of a relation is the set of all second elements of the ordered pairs in the relation. The range is a subset of the codomain and represents all the possible outputs of the relation for any input in the domain. The domain and codomain help to determine the range of the relation.
  3. Type of Relation: The domain and codomain can be used to determine the type of relation. For example, if the domain and codomain are the same set, then the relation is called an endorelation. If the domain and codomain are different sets, then the relation is called a binary relation.

Conclusion:

In conclusion, the domain and codomain of a relation are essential concepts that allow us to define and understand relations in mathematics. They help to ensure that the relation is well-defined, and they provide information about the range of the relation and the type of relation. By properly defining the domain and codomain, we can gain insights into the nature of the relation and its properties.