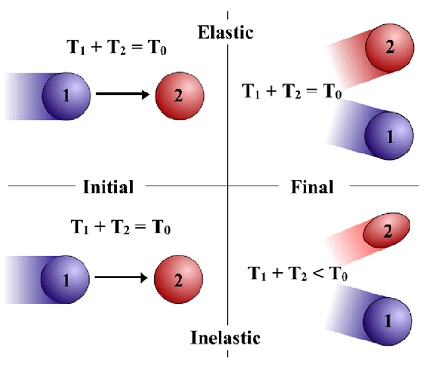
In physics, collisions between objects can be classified as either elastic or inelastic, based on how the kinetic energy of the system is conserved.
An elastic collision is one in which the kinetic energy of the system is conserved, meaning that the total kinetic energy of the colliding objects before the collision is equal to the total kinetic energy of the objects after the collision. In an elastic collision, both the momentum and kinetic energy of the system are conserved. Examples of elastic collisions include the collision of two billiard balls, where both balls bounce off each other without losing any kinetic energy.
In contrast, an inelastic collision is one in which the kinetic energy of the system is not conserved, meaning that some of the kinetic energy is converted into other forms of energy, such as heat or sound. In an inelastic collision, momentum is still conserved, but the total kinetic energy of the system is not. An example of an inelastic collision is a car crash, where the kinetic energy of the moving car is partially converted into other forms of energy upon collision, such as heat, sound, and deformation of the car.
It is important to note that the distinction between elastic and inelastic collisions is not always clear-cut, as some collisions may have characteristics of both. For example, a collision between two objects with some degree of elasticity may result in some loss of kinetic energy due to deformation, but still be considered predominantly elastic if the loss of energy is small compared to the total energy of the system.
What is Required Mechanics Elastic and Inelastic collisions
In Required Mechanics, the study of elastic and inelastic collisions is an important part of understanding the conservation of momentum and energy in physical systems.
In an elastic collision, the conservation of momentum and kinetic energy can be expressed mathematically using the following equations:
m1v1i + m2v2i = m1v1f + m2v2f (conservation of momentum) 1/2 m1v1i^2 + 1/2 m2v2i^2 = 1/2 m1v1f^2 + 1/2 m2v2f^2 (conservation of kinetic energy)
where m1 and m2 are the masses of the objects involved in the collision, v1i and v2i are their initial velocities, and v1f and v2f are their final velocities.
In an inelastic collision, the conservation of momentum is still valid, but the conservation of kinetic energy is not. In this case, the loss of kinetic energy is typically due to the deformation of the colliding objects or the conversion of kinetic energy into other forms of energy. The final velocities of the objects after an inelastic collision can be calculated using the conservation of momentum equation:
m1v1i + m2v2i = (m1 + m2)vf
where vf is the final velocity of both objects after the collision.
In both elastic and inelastic collisions, the relative velocity of the objects before and after the collision can also be calculated using the equations:
v1f – v2f = -(v1i – v2i) (for an elastic collision) v1f – v2f = -e(v1i – v2i) (for an inelastic collision)
where e is the coefficient of restitution, which is a measure of the elasticity of the collision. The coefficient of restitution ranges between 0 and 1, where a value of 1 represents a perfectly elastic collision, and a value of 0 represents a completely inelastic collision.
When is Required Mechanics Elastic and Inelastic collisions
Required Mechanics considers elastic and inelastic collisions when analyzing the motion of objects that collide with each other. Elastic and inelastic collisions occur when two objects collide and exert forces on each other.
An elastic collision occurs when the kinetic energy of the system is conserved, meaning that the total kinetic energy of the colliding objects before the collision is equal to the total kinetic energy of the objects after the collision. In an elastic collision, both the momentum and kinetic energy of the system are conserved. Examples of elastic collisions include the collision of two billiard balls or the collision of two ideal gas particles.
In contrast, an inelastic collision occurs when the kinetic energy of the system is not conserved, meaning that some of the kinetic energy is converted into other forms of energy, such as heat or sound. In an inelastic collision, momentum is still conserved, but the total kinetic energy of the system is not. An example of an inelastic collision is a car crash or the collision of two pieces of clay.
The distinction between elastic and inelastic collisions is important because it determines how much of the initial kinetic energy is transferred between the colliding objects, and how much is lost to other forms of energy. This can have important implications for the motion of the objects and the forces exerted on them during the collision.
Where is Required Mechanics Elastic and Inelastic collisions
Required Mechanics is a branch of physics that studies the motion of objects and the forces that act on them. The concepts of elastic and inelastic collisions are used in Required Mechanics to analyze the behavior of objects that collide with each other.
Elastic and inelastic collisions occur in a wide range of physical systems, from the microscopic scale of atoms and molecules, to the macroscopic scale of everyday objects like cars and billiard balls. Elastic collisions are commonly observed in the behavior of ideal gases, where the particles collide with each other without losing kinetic energy. Inelastic collisions are often observed in the behavior of solid objects, where the objects deform upon collision and some of the initial kinetic energy is converted into other forms of energy, such as heat or sound.
The study of elastic and inelastic collisions is important in a variety of fields, including engineering, materials science, and astrophysics. For example, engineers use the principles of Required Mechanics to design crash test dummies and safety features in cars to minimize the forces and injuries experienced by passengers during collisions. Materials scientists use these principles to develop new materials that can absorb energy and deform without breaking during collisions. Astrophysicists use these principles to study the behavior of colliding stars and galaxies in the universe.
How is Required Mechanics Elastic and Inelastic collisions
Required Mechanics describes elastic and inelastic collisions using the principles of conservation of momentum and energy. In both types of collisions, the total momentum of the colliding objects is conserved, meaning that the sum of the momentum of the objects before the collision is equal to the sum of the momentum of the objects after the collision.
In an elastic collision, the kinetic energy of the colliding objects is also conserved. This means that the total kinetic energy of the objects before the collision is equal to the total kinetic energy of the objects after the collision. The conservation of kinetic energy is related to the elasticity of the objects involved in the collision. In an ideal elastic collision, the objects bounce off each other without any loss of kinetic energy.
In contrast, in an inelastic collision, the kinetic energy of the colliding objects is not conserved. Some of the initial kinetic energy is converted into other forms of energy, such as heat, sound, or deformation of the objects. The amount of kinetic energy lost depends on the materials and the conditions of the collision.
To analyze the motion of objects during elastic and inelastic collisions, Required Mechanics uses mathematical equations based on the conservation principles. For example, the equations for conservation of momentum and kinetic energy can be used to calculate the final velocities of the colliding objects after the collision.
Overall, Required Mechanics provides a framework for understanding the behavior of objects during collisions and the transfer of energy between them. This understanding has many practical applications, including designing safety features in vehicles, developing materials that can absorb energy during impacts, and analyzing the behavior of stars and planets during collisions.
Production of Mechanics Elastic and Inelastic collisions
The production of mechanics in elastic and inelastic collisions involves understanding the forces and energy involved in the collision process. Elastic collisions involve collisions where the total kinetic energy of the system is conserved, while inelastic collisions involve collisions where the total kinetic energy is not conserved and some of the initial kinetic energy is converted into other forms of energy.
In order to understand the production of mechanics in elastic and inelastic collisions, several key principles are used:
- Conservation of momentum: This principle states that the total momentum of a system is conserved, meaning that the sum of the momenta of all the objects in a system is constant before and after the collision.
- Conservation of kinetic energy: In elastic collisions, the total kinetic energy of the system is conserved, meaning that the sum of the kinetic energies of all the objects in the system is constant before and after the collision. In inelastic collisions, some of the initial kinetic energy is lost as it is converted into other forms of energy.
- Impulse-momentum theorem: This theorem states that the change in momentum of an object is equal to the impulse (force times time) acting on it.
Using these principles, we can analyze the production of mechanics in elastic and inelastic collisions. For example, in an elastic collision, if two objects collide and bounce back off each other with the same speed, the total kinetic energy of the system is conserved, and the total momentum of the system is also conserved. In contrast, in an inelastic collision, the objects may stick together after the collision, and some of the initial kinetic energy is converted into heat or sound energy, reducing the total kinetic energy of the system.
The study of the production of mechanics in elastic and inelastic collisions has many practical applications, such as in designing safety features for cars or predicting the behavior of objects in space. Understanding the forces and energy involved in these collisions can help us to better predict and control the outcomes of these events.
Case Study on Mechanics Elastic and Inelastic collisions
One common case study in mechanics involving elastic and inelastic collisions is the behavior of billiard balls during a game of pool. When two balls collide on the pool table, they undergo a collision that can be either elastic or inelastic, depending on the materials of the balls and the conditions of the collision.
In an elastic collision between two billiard balls, the total kinetic energy of the system is conserved, and the balls bounce off each other with the same speed and direction as before the collision. The momentum of each ball is also conserved, meaning that the sum of the momenta of the balls before and after the collision is equal. In this case, the energy transferred from one ball to the other is done so without any loss, resulting in a clean, precise transfer of energy.
In contrast, in an inelastic collision between two billiard balls, the balls stick together after the collision, and some of the initial kinetic energy is lost as it is converted into other forms of energy, such as heat or sound. This type of collision is more likely to occur when the balls are made of a softer material or are struck with less force. In an inelastic collision, the momentum of the system is still conserved, but the total kinetic energy is not.
The behavior of billiard balls during a game of pool can be analyzed using the principles of mechanics, such as conservation of momentum and kinetic energy. This understanding can help players to predict and control the movements of the balls during a game. It also has practical applications in the design of safety features for cars and other machinery, where understanding the behavior of colliding objects is critical to preventing accidents and minimizing damage.
White paper on Mechanics Elastic and Inelastic collisions
Introduction:
Mechanics is the branch of physics that studies the motion of objects under the influence of forces. Elastic and inelastic collisions are fundamental concepts in mechanics that describe the behavior of objects during collisions. Elastic collisions involve collisions where the total kinetic energy of the system is conserved, while inelastic collisions involve collisions where the total kinetic energy is not conserved and some of the initial kinetic energy is converted into other forms of energy. This white paper will explore the key concepts of elastic and inelastic collisions and their practical applications.
Elastic Collisions:
In an elastic collision, the total kinetic energy of the system is conserved, meaning that the sum of the kinetic energies of all the objects in the system is constant before and after the collision. The momentum of each object is also conserved, meaning that the sum of the momenta of all the objects in the system is constant before and after the collision.
In an ideal elastic collision, the objects bounce off each other without any loss of kinetic energy. This type of collision is rare in the real world, but it is useful for simplifying calculations and understanding the behavior of objects during collisions. In most elastic collisions, there is some loss of kinetic energy due to factors such as friction, air resistance, or deformation of the objects.
Inelastic Collisions:
In an inelastic collision, some of the initial kinetic energy is lost as it is converted into other forms of energy, such as heat, sound, or deformation of the objects. The amount of kinetic energy lost depends on the materials and conditions of the collision.
In some cases, the objects may stick together after the collision, resulting in a perfectly inelastic collision. In this case, the total kinetic energy of the system is not conserved, but the momentum of the system is still conserved.
Applications:
The principles of elastic and inelastic collisions have many practical applications. For example, in the design of safety features for cars, understanding the behavior of colliding objects is critical to preventing accidents and minimizing damage. Inelastic collisions can be used to absorb the energy of impacts and reduce the risk of injury or damage.
The principles of elastic and inelastic collisions are also used in fields such as materials science and engineering. For example, the behavior of materials during impacts can be studied to develop materials that are more resistant to damage or that can absorb energy more effectively.
Conclusion:
Elastic and inelastic collisions are fundamental concepts in mechanics that describe the behavior of objects during collisions. Elastic collisions involve collisions where the total kinetic energy of the system is conserved, while inelastic collisions involve collisions where some of the initial kinetic energy is lost as it is converted into other forms of energy. The principles of elastic and inelastic collisions have many practical applications, including in the design of safety features for cars, the development of materials that can absorb energy during impacts, and the study of the behavior of objects in space.