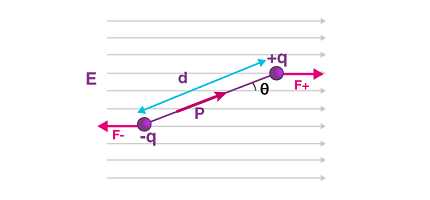
In a uniform electrostatic field, an electric dipole experiences a torque that tends to align the dipole moment vector with the direction of the field. The magnitude of the torque is given by the vector product of the dipole moment vector and the electric field vector.

If the dipole moment vector is not aligned with the field direction, the dipole will experience a net torque that tends to rotate it until it becomes aligned with the field. Once the dipole moment is aligned with the field direction, the torque on the dipole will be zero, and the dipole will experience no further rotation.

The potential energy of an electric dipole in a uniform electrostatic field is given by the dot product of the dipole moment vector and the electric field vector. The potential energy is minimum when the dipole moment is aligned with the field direction, and maximum when the dipole moment is perpendicular to the field direction.

Overall, the behavior of electric dipoles in a uniform electrostatic field can be explained in terms of the interaction between the dipole moment and the electric field. The torque and potential energy depend on the relative orientation of the dipole moment and the electric field, and tend to align the dipole moment with the field direction.

What is Required Electrical dipoles in a uniform electrostatic field

The requirements for an electric dipole to experience a torque in a uniform electrostatic field are:

1. Non-zero dipole moment: The electric dipole must have a non-zero dipole moment, which is a measure of the separation of positive and negative charges in the dipole. If the dipole moment is zero, then there will be no torque acting on the dipole in the uniform electric field.
2. Uniform electric field: The electric field must be uniform, which means that the magnitude and direction of the field should be the same at all points in the region of interest. If the field is not uniform, then different parts of the dipole will experience different forces, and the dipole will not experience a net torque.
3. Orientation of the dipole: The orientation of the dipole moment relative to the direction of the electric field determines the magnitude and direction of the torque acting on the dipole. If the dipole moment is parallel to the field, then there will be no torque acting on the dipole. If the dipole moment is perpendicular to the field, then the torque will be maximum.

In summary, for an electric dipole to experience a torque in a uniform electrostatic field, it needs to have a non-zero dipole moment, the electric field needs to be uniform, and the orientation of the dipole moment needs to be non-parallel to the direction of the field.

When is Required Electrical dipoles in a uniform electrostatic field

Electric dipoles in a uniform electrostatic field are encountered in many different contexts in physics and engineering. Some examples include:

1. Molecular interactions: Many molecules have electric dipole moments due to the separation of charges within the molecule. When these molecules are placed in a uniform electric field, they experience a torque that tends to align the dipole moment with the field direction. This is important for understanding molecular interactions and the behavior of polar molecules in electric fields.
2. Capacitors: A capacitor consists of two conducting plates separated by a dielectric material. When a voltage is applied to the plates, an electric field is created between the plates. If the dielectric material has a non-zero dielectric constant, it can become polarized and create an electric dipole moment. This dipole moment experiences a torque in the uniform electric field between the plates, which can lead to mechanical stress and deformation of the capacitor.
3. Particle accelerators: Particle accelerators use electric fields to accelerate charged particles. In order to create a uniform electric field over a large region, the accelerator may use a series of electrodes or magnets that generate an alternating gradient of electric field strength. Charged particles passing through this region experience a torque due to their dipole moment, which can cause them to align with the field direction and increase their acceleration.

Overall, electric dipoles in a uniform electrostatic field are important for understanding many physical and engineering phenomena, and they are encountered in a wide range of applications.

Where is Required Electrical dipoles in a uniform electrostatic field

Electric dipoles in a uniform electrostatic field can be found in various locations and systems in physics and engineering. Some examples include:

1. Molecular systems: Many molecular systems, such as water molecules or organic molecules, have electric dipole moments due to the separation of charges within the molecule. When these molecules are placed in a uniform electrostatic field, they experience a torque that tends to align the dipole moment with the field direction. This is important for understanding molecular interactions, such as the behavior of polar molecules in electric fields or the interaction between molecules in a solution.
2. Capacitors: Capacitors are commonly used in electronic circuits to store and discharge electrical energy. A capacitor consists of two conducting plates separated by a dielectric material. When a voltage is applied to the plates, an electric field is created between the plates. If the dielectric material has a non-zero dielectric constant, it can become polarized and create an electric dipole moment. This dipole moment experiences a torque in the uniform electric field between the plates, which can lead to mechanical stress and deformation of the capacitor.
3. Particle accelerators: Particle accelerators use electric fields to accelerate charged particles. In order to create a uniform electric field over a large region, the accelerator may use a series of electrodes or magnets that generate an alternating gradient of electric field strength. Charged particles passing through this region experience a torque due to their dipole moment, which can cause them to align with the field direction and increase their acceleration.
4. Ion traps: Ion traps are used in mass spectrometry and other applications to trap and manipulate ions using electric and magnetic fields. In a uniform electrostatic field, an ion with a non-zero dipole moment will experience a torque that tends to align its dipole moment with the field direction. This can be used to selectively trap ions with specific dipole moments or to manipulate the motion of trapped ions.

Overall, electric dipoles in a uniform electrostatic field can be found in a wide range of systems and locations in physics and engineering, and they play an important role in understanding the behavior of these systems.

How is Required Electrical dipoles in a uniform electrostatic field

The behavior of electric dipoles in a uniform electrostatic field can be described using principles of electrostatics and classical mechanics.

When an electric dipole with a non-zero dipole moment is placed in a uniform electrostatic field, the dipole experiences a torque that tends to align its dipole moment with the field direction. This torque is given by the cross product of the dipole moment vector and the electric field vector, which can be expressed mathematically as:

τ = p x E

where τ is the torque acting on the dipole, p is the dipole moment vector, and E is the electric field vector.

The magnitude of the torque is proportional to the magnitude of the dipole moment and the magnitude of the electric field, and the direction of the torque is perpendicular to both the dipole moment vector and the electric field vector.

The torque on the dipole can cause it to rotate around an axis perpendicular to both the dipole moment vector and the electric field vector. The rotational motion of the dipole can be described using the principles of classical mechanics, such as Newton’s laws of motion and rotational dynamics.

For example, if the dipole is free to rotate around a fixed axis, the torque on the dipole will cause it to undergo rotational motion with an angular acceleration that is proportional to the torque and inversely proportional to the moment of inertia of the dipole. The resulting angular velocity of the dipole can be determined using equations of rotational kinematics.

Overall, the behavior of electric dipoles in a uniform electrostatic field can be analyzed using principles of electrostatics, classical mechanics, and rotational dynamics. By understanding the torque and rotational motion of the dipole, we can gain insight into the behavior of many physical and engineering systems that involve electric dipoles and uniform electrostatic fields.

Nomenclature of Electrical dipoles in a uniform electrostatic field

The nomenclature used to describe electric dipoles in a uniform electrostatic field typically includes the following terms:

1. Electric dipole moment: The electric dipole moment (p) is a vector quantity that describes the separation of charges within an electric dipole. It is defined as the product of the magnitude of the charge separation (q) and the distance between the charges (d). Mathematically, the dipole moment vector is given by p = qd.
2. Electric field: The electric field (E) is a vector quantity that describes the strength and direction of the electric force experienced by a charged particle at a given point in space. In a uniform electrostatic field, the electric field has the same strength and direction at all points in space.
3. Torque: The torque (τ) is a vector quantity that describes the rotational force experienced by an object when a force is applied at a distance from the object’s center of mass. In the context of electric dipoles in a uniform electrostatic field, the torque is the force that causes the dipole to rotate around an axis perpendicular to both the dipole moment vector and the electric field vector.
4. Moment of inertia: The moment of inertia (I) is a scalar quantity that describes the resistance of an object to rotational motion. In the context of electric dipoles in a uniform electrostatic field, the moment of inertia is a property of the dipole that determines how easily it can be rotated by the torque.
5. Angular velocity: The angular velocity (ω) is a vector quantity that describes the rotational speed of an object around an axis. In the context of electric dipoles in a uniform electrostatic field, the angular velocity describes the rate at which the dipole is rotating in response to the torque.

Overall, these terms are used to describe the behavior of electric dipoles in a uniform electrostatic field and to analyze the rotational motion of the dipole. By understanding these concepts and their relationships, we can gain insight into the behavior of many physical and engineering systems that involve electric dipoles and uniform electrostatic fields.

Case Study on Electrical dipoles in a uniform electrostatic field

A common application of electric dipoles in a uniform electrostatic field is in the design and operation of electric motors. Electric motors rely on the interaction between electric fields and electric currents to produce mechanical motion.

In an electric motor, a coil of wire is placed within a magnetic field, which creates an electric current in the wire. The electric current in the coil produces its own magnetic field, which interacts with the external magnetic field to produce a rotational force on the coil.

This rotational force is produced through the interaction of electric dipoles and a uniform electrostatic field. The electric current in the wire generates an electric dipole moment, and the external magnetic field produces a uniform electrostatic field. The resulting torque on the electric dipole moment causes the coil to rotate within the magnetic field.

The rotational motion of the coil is determined by the torque on the electric dipole moment and the moment of inertia of the coil. The torque is proportional to the strength of the magnetic field and the magnitude of the electric dipole moment, and the moment of inertia is determined by the mass and geometry of the coil.

By controlling the strength and direction of the magnetic field, it is possible to control the rotational motion of the electric motor. Electric motors are widely used in many applications, such as in vehicles, appliances, and machinery, and their performance can be optimized through the careful design of the electric dipole and magnetic fields.

In summary, the study of electric dipoles in a uniform electrostatic field is essential for the design and operation of electric motors and many other physical and engineering systems that rely on the interaction of electric and magnetic fields. Understanding the principles of electrostatics and rotational dynamics can help engineers and scientists optimize the performance and efficiency of these systems.

White paper on Electrical dipoles in a uniform electrostatic field

Introduction:

An electrical dipole is a pair of equal and opposite electrical charges separated by a distance, which creates a dipole moment. The electric dipole moment is the product of the distance between the charges and the magnitude of the charges. When a dipole is placed in a uniform electric field, it experiences a torque that aligns the dipole moment with the field direction.

In this white paper, we will discuss the behavior of electrical dipoles in a uniform electrostatic field, including the torque experienced by the dipole, the potential energy of the dipole in the field, and the electric field produced by the dipole.

Torque on an electrical dipole in a uniform electrostatic field:

When a dipole is placed in a uniform electrostatic field, the dipole experiences a torque that tends to align the dipole moment with the field direction. The torque on the dipole is given by the cross product of the dipole moment and the electric field:

τ = p × E

where τ is the torque, p is the dipole moment, and E is the electric field. The torque is maximum when the dipole moment is perpendicular to the electric field and zero when the dipole moment is parallel to the electric field.

The potential energy of an electrical dipole in a uniform electrostatic field:

The potential energy of an electrical dipole in a uniform electrostatic field is given by the dot product of the dipole moment and the electric field:

U = -p ⋅ E

where U is the potential energy, p is the dipole moment, and E is the electric field. The potential energy is minimum when the dipole moment is aligned with the electric field and maximum when the dipole moment is perpendicular to the electric field.

The electric field produced by an electrical dipole:

An electrical dipole produces an electric field that is proportional to the dipole moment and inversely proportional to the cube of the distance from the dipole:

E = (1/4πε₀) [(3p⋅r̂r̂ – p)/r³]

where E is the electric field, ε₀ is the permittivity of free space, p is the dipole moment, r is the distance from the dipole, and r̂ is the unit vector in the direction of r. The electric field produced by an electrical dipole is strongest at points close to the dipole and weakens rapidly with increasing distance.

Conclusion:

In conclusion, electrical dipoles in a uniform electrostatic field experience a torque that aligns the dipole moment with the field direction. The potential energy of the dipole in the field is minimum when the dipole moment is aligned with the electric field and maximum when the dipole moment is perpendicular to the electric field. An electrical dipole produces an electric field that is proportional to the dipole moment and inversely proportional to the cube of the distance from the dipole. These principles have important applications in fields such as electromagnetism, molecular physics, and materials science.