Equation of a circle in various forms

Equation of a circle in various forms, JEE Mathematics Analytical Geometry, , , , , , ,

Circle

A circle is a shape comprising of all places in a plane that are at a given separation from a given point, the middle. Proportionally, it is the bend followed out by a that maneuvers in a plane so that its separation from a given point is steady. The distance between any place of the circle and the middle is known as the range. Normally, the span is expected to be a positive number. A circle with r=0 (a solitary point) is a ruffian case. This article is about circles in Euclidean calculation, and, specifically, the Euclidean plane, aside from where generally noted.

In particular, a circle is a basic shut bend that partitions the plane into two districts: an inside and an outside. In regular use, the expression “circle” might be utilized reciprocally to allude to either the limit of the figure, or to the entire figure including its inside; in severe specialized utilization, the circle is just the limit and the entire figure is known as a plate.

A circle may likewise be characterized as an extraordinary sort of oval in which the two foci are incidental, the capriciousness is 0, and the semi-major and semi-minor tomahawks are equivalent; or the two-layered shape encasing the most region per unit border squared, utilizing math of varieties.

Equation

In science, a condition is a recipe that communicates the equity of two articulations, by interfacing them with the equivalents sign =. The word condition and its cognates in different dialects might have quietly various implications; for instance, in French a équation is characterized as containing at least one factors, while in English, any all around shaped recipe comprising of two articulations related with an equivalents sign is a condition.

Settling a condition containing factors comprises of figuring out which upsides of the factors make the fairness valid. The factors for which the condition must be settled are additionally called questions, and the upsides of the questions that fulfill the uniformity are called arrangements of the situation. There are two sorts of conditions: personalities and restrictive conditions. A personality is valid for all upsides of the factors. A contingent condition is just valid for specific upsides of the factors.

A condition is composed as two articulations, associated by an equivalents sign (“=”). The articulations on the different sides of the equivalents sign are known as the “left-hand side” and “right-hand side” of the situation. Regularly the right-hand side of a situation is thought to be zero. Accepting this doesn’t decrease the consensus, as this can be acknowledged by taking away the right-hand side from the two sides.

The most widely recognized sort of condition is a polynomial condition (usually called likewise a mathematical condition) in which the different sides are polynomials. The sides of a polynomial condition contain at least one terms. For instance, the condition

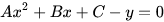
has left-hand side Ax^{2}+Bx+C-y}, which has four terms, and right-hand side 0 consisting of just one term. The names of the variables suggest that x and y are unknowns, and that A, B, and C are parameters, but this is normally fixed by the context (in some contexts, y may be a parameter, or A, B, and C may be ordinary variables).

A condition is closely resembling a scale into which loads are set. At the point when equivalent loads of something (e.g., grain) are put into the two dish, the two loads make the scale be in balance and are supposed to be equivalent. On the off chance that an amount of grain is eliminated from one skillet of the equilibrium, an equivalent measure of grain should be taken out from the other container to keep the scale in balance. All the more by and large, a condition stays in balance in the event that a similar activity is performed on its the two sides.

In Cartesian calculation, conditions are utilized to depict mathematical figures. As the situations that are thought of, like implied conditions or parametric conditions, have limitlessly numerous arrangements, the goal is presently unique: rather than giving the arrangements unequivocally or counting them, which is unimaginable, one purposes conditions for concentrating on properties of figures. This is the beginning thought of arithmetical calculation, a significant area of science.

Variable based math concentrates on two fundamental groups of conditions: polynomial conditions and, among them, the extraordinary instance of direct conditions. At the point when there is just a single variable, polynomial conditions have the structure P(x) = 0, where P is a polynomial, and straight conditions have the structure hatchet + b = 0, where an and b are boundaries. To address conditions from one or the other family, one purposes algorithmic or mathematical methods that begin from direct polynomial math or numerical examination. Variable based math additionally concentrates on Diophantine conditions where the coefficients and arrangements are whole numbers. The strategies utilized are unique and come from number hypothesis. These conditions are troublesome overall; one frequently look just to track down the presence or nonappearance of an answer, and, on the off chance that they exist, to count the quantity of arrangements.

Differential conditions are conditions that include at least one capabilities and their subsidiaries. They are tackled by finding an articulation for the capability that doesn’t include subordinates. Differential conditions are utilized to display processes that include the paces of progress of the variable, and are utilized in regions like material science, science, science, and financial matters.

The “=” image, which shows up in each situation, was designed in 1557 by Robert Recorde, who thought about that nothing could be more equivalent than equal straight lines with a similar length.

Circle

A circle is a round, two-dimensional shape. All points on the edge of the circle are at the same distance from the center.

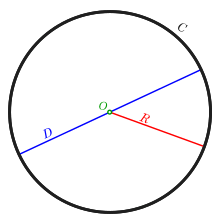
The radius of a circle is a line from the center of the circle to a point on the side. Mathematicians use the letter r for the length of a circle’s radius. The center of a circle is the point in the very middle. It is often written as {\displaystyle O}.

The diameter (meaning “all the way across”) of a circle is a straight line that goes from one side to the opposite and right through the center of the circle. Mathematicians use the letter {\displaystyle d} for the length of this line. The diameter of a circle is equal to twice its radius ({\displaystyle d} equals 2 times r): {\displaystyle d=2r}

The circumference (meaning “all the way around”) of a circle is the line that goes around the center of the circle. Mathematicians use the letter {\displaystyle c} for the length of this line.

The number π (written as the Greek letter pi) is a very useful number. It is the length of the circumference divided by the length of the diameter ({\displaystyle \pi } equals {\displaystyle c} divided by {\displaystyle d}). As a fraction the number {\displaystyle \pi } is equal to about {\displaystyle {\frac {22}{7}}} or {\displaystyle {\frac {355}{113}}} (which is closer) and as a number it is about 3.1415926536.

{\displaystyle \pi ={\frac {c}{d}}}
{\displaystyle \therefore {\textrm {(therefore)}}}{\displaystyle c=2\pi r}{\displaystyle c=\pi d}

The area, {\displaystyle A}, inside a circle is equal to the radius multiplied by itself, then multiplied by {\displaystyle \pi } ({\displaystyle A} equals {\displaystyle \pi } times r times 2{\displaystyle A=\pi r^{2}}

Area of a circle

In calculation, the region encased by a circle of sweep r is πr2. Here the Greek letter π addresses the steady proportion of the perimeter of any circle to its distance across, around equivalent to 3.14159.

One technique for inferring this recipe, which began with Archimedes, includes seeing the circle as the constraint of a succession of normal polygons with a rising number of sides. The region of an ordinary polygon is a portion of its border increased by the separation from its middle to its sides, and on the grounds that the succession keeps an eye on a circle, the comparing equation that the region is a portion of the periphery times the sweep specifically, A = 1/2 × 2πr × r, holds for a circle.

Where is Equation of a circle in various forms

The equation of a circle can be written in various forms, including:

  1. Standard Form: (x – h)^2 + (y – k)^2 = r^2 This form represents a circle with center (h, k) and radius r.
  2. General Form: Ax^2 + Ay^2 + Bx + Cy + D = 0 This form represents a circle with center (-B/2A, -C/2A) and radius sqrt((B^2 + C^2)/4A^2 – D/A).
  3. Parametric Form: x = r cos(t), y = r sin(t) This form represents a circle with center at the origin and radius r, where t is the parameter.
  4. Polar Form: r = a + b cos(theta) or r = a + b sin(theta) This form represents a circle with center at (a, 0) or (0, a) and radius b.
  5. Center-Radius Form: (x – a)^2 + (y – b)^2 = r^2 This form represents a circle with center (a, b) and radius r.

These different forms are useful in different situations depending on the information that is known about the circle.

How is Equation of a circle in various forms

The equation of a circle can be derived using the Pythagorean theorem, which states that in a right triangle, the sum of the squares of the two shorter sides is equal to the square of the longest side (hypotenuse).

Consider a circle with center (h, k) and radius r. Any point on the circle can be represented as (x, y). Using the distance formula, we can write:

d = sqrt((x – h)^2 + (y – k)^2)

where d is the distance from (x, y) to the center of the circle. Since (x, y) lies on the circle, d is equal to the radius r.

Substituting r for d, we get:

sqrt((x – h)^2 + (y – k)^2) = r

Squaring both sides, we get:

(x – h)^2 + (y – k)^2 = r^2

This is the standard form of the equation of a circle, which represents a circle with center (h, k) and radius r.

The other forms of the equation of a circle can be derived by manipulating this standard form.

Squaring the circle

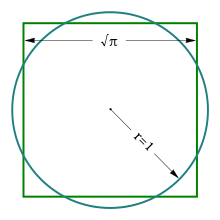
Squaring the circle is an issue in calculation previously proposed in Greek math. It is the test of developing a square with the region of a circle by utilizing just a limited number of steps with a compass and straightedge. The trouble of the issue brought up the issue of whether determined sayings of Euclidean math concerning the presence of lines and circles inferred the presence of such a killjoy.

In 1882, the undertaking was demonstrated to be unimaginable, as an outcome of the Lindemann-Weierstrass hypothesis, which demonstrates that pi is a supernatural number. That is,pi isn’t the foundation of any polynomial with reasonable coefficients. It had been known for a really long time that the development would be incomprehensible if pi were supernatural, however that reality was not demonstrated until 1882. Estimated developments with some random non-amazing precision exist, and numerous such developments have been found.

Regardless of the verification that it is unimaginable, endeavors to square the circle have been normal in pseudomathematics (for example crafted by numerical wrenches). The maxim “squaring the circle” is some of the time utilized as a similitude for attempting to do the impossible. The term quadrature of the circle is some of the time utilized as an equivalent for squaring the circle, however it might likewise allude to estimated or mathematical strategies for tracking down the region of a circle.

Equation of a Circle

A circle is the set of all points in the plane which maintains a fixed finite distance r from a fixed point O=(a,b). Here O is called the center, and r is called the radius of that circle. The use of the equation of a circle is prevalent throughout coordinate geometry problems.

General Equation of Circle

The equation of any conic can be expressed as

ax2+2hxy+by2+2gx+2fy+c=0.

However, the condition for the equation to represent a circle is a = b and ℎ = 0. Then the general equation of the circle becomes

x2+y2+2gx+2fy+c=0.

Unfortunately, it can be difficult to decipher any meaningful properties about a given circle from its general equation, so completing the square allows quick conversion to the standard form, which contains values for the center and radius of the circle.