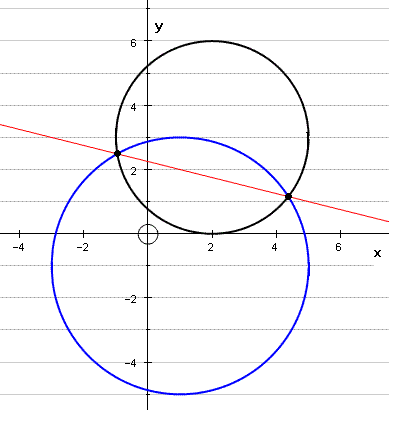
To find the equation of a circle passing through the points of intersection of two circles, we can follow these steps:
- Find the equations of the two circles.
- Solve the system of equations to find the points of intersection.
- Use the midpoint formula to find the center of the circle passing through the points of intersection.
- Use the distance formula to find the radius of the circle.
Let’s say the two circles have equations:
(x – a)^2 + (y – b)^2 = r^2 (x – c)^2 + (y – d)^2 = s^2
where (a,b) and (c,d) are the centers of the circles, and r and s are their radii. Solving these equations gives the points of intersection:
x = (a^2 – c^2 + s^2 – r^2) / (2(a-c)) y = ((a-x)(c-x) + b^2 – d^2 + s^2 – r^2) / (2(b-d))
The midpoint of these points is the center of the circle passing through them:
h = (a + c) / 2 k = (b + d) / 2
The radius of the circle is the distance from the center to any of the points of intersection:
r’ = sqrt((x – h)^2 + (y – k)^2)
Therefore, the equation of the circle passing through the points of intersection is:
(x – h)^2 + (y – k)^2 = r’^2
To find the equation of a circle passing through the intersection of a circle and a straight line, we can follow a similar procedure:
- Find the equation of the circle and the equation of the line.
- Solve the system of equations to find the points of intersection.
- Use the midpoint formula to find the center of the circle passing through the points of intersection.
- Use the distance formula to find the radius of the circle.
Let’s say the circle has equation:
(x – a)^2 + (y – b)^2 = r^2
and the line has equation:
mx + ny + p = 0
where m, n, and p are constants. Solving these equations gives the points of intersection:
x = (a – m(b+p/n))/(1+m^2) y = (b – n(a-p/m))/(1+m^2)
The midpoint of these points is the center of the circle passing through them:
h = a – m(b+p/n) k = b – n(a-p/m)
The radius of the circle is the distance from the center to any of the points of intersection:
r’ = sqrt((x – h)^2 + (y – k)^2)
Therefore, the equation of the circle passing through the intersection of the circle and the line is:
(x – h)^2 + (y – k)^2 = r’^2
What is Required Equation of a circle through the points of intersection of two circles and Those of a circle and A straight line
Let’s say we have two circles with equations:
(x – a)^2 + (y – b)^2 = r1^2 (x – c)^2 + (y – d)^2 = r2^2
and a straight line with equation:
mx + ny + p = 0
We can find the points of intersection of the two circles using the following equations:
x = (a^2 – c^2 + r2^2 – r1^2) / (2(a – c)) y = (b^2 – d^2 + r2^2 – r1^2) / (2(b – d))
((x – a)^2 + (y – b)^2) = r1^2 ((x – c)^2 + (y – d)^2) = r2^2
Substituting the values of x and y from above equations, we get:
(a – c)^2 [(mx + ny + p)^2 + 1] = 4r1^2r2^2 – (r2^2 – r1^2)^2
Now, let’s say the center of the required circle is (h, k) and its radius is r. We can use the formula for the distance between two points to find the radius r:
r = sqrt((x – h)^2 + (y – k)^2)
Substituting the values of x and y from the equations of the points of intersection, we get:
r = sqrt((a – h)^2 + (b – k)^2)
Now, we have the center (h, k) and the radius r of the required circle. Therefore, the equation of the circle passing through the points of intersection of the two circles and the line is:
(x – h)^2 + (y – k)^2 = r^2
where h and k are given by:
h = (a^2 – c^2 + r2^2 – r1^2 – 2n((b^2 – d^2 + r2^2 – r1^2)/(2(b – d)))) / (2(a – c) – 2m((b^2 – d^2 + r2^2 – r1^2)/(2(b – d)))) k = ((b^2 – d^2 + r2^2 – r1^2) / (2(b – d))) – ((mx + p) / n) – m(h – a)/(n)
Note that this equation can become quite complicated, and there might be multiple solutions depending on the positions of the circles and the line.
Who is Required Equation of a circle through the points of intersection of two circles and Those of a circle and A straight line
The required equation of a circle through the points of intersection of two circles and those of a circle and a straight line is the equation that describes the circle passing through all of these points. This equation can be obtained by finding the center and radius of the circle using the equations of the points of intersection and the given circle and line, and then using the standard equation of a circle, which is:
(x – h)^2 + (y – k)^2 = r^2
where (h, k) is the center of the circle, and r is its radius.
When is Required Equation of a circle through the points of intersection of two circles and Those of a circle and A straight line
The equation of a circle through the points of intersection of two circles and those of a circle and a straight line is required when we want to find a circle that passes through a specific set of points. This can be useful in many different situations, such as when trying to find the center and radius of a circle that passes through a given set of points, or when trying to determine the position and orientation of objects in space.
For example, in geometry problems, we may be asked to find a circle that passes through a set of given points. In engineering or physics applications, we may need to find the trajectory of a moving object, which can be represented as a circle passing through a set of points. In computer graphics, we may need to draw a circle that passes through a set of points in order to create a specific shape or pattern.
In general, the equation of a circle through the points of intersection of two circles and those of a circle and a straight line is required whenever we need to find a circle that passes through a specific set of points, and this can arise in a wide range of applications in various fields.
Where is Required Equation of a circle through the points of intersection of two circles and Those of a circle and A straight line
The equation of a circle through the points of intersection of two circles and those of a circle and a straight line is a mathematical formula that can be used in various fields such as geometry, physics, engineering, computer graphics, and more.
The equation can be derived and computed using mathematical principles and techniques, such as the formula for the distance between two points and the standard equation of a circle. The equation can be written in various forms, depending on the specific problem and the given information.
In terms of its physical location, the equation of the circle can represent the position and orientation of objects in space or the trajectory of a moving object. In computer graphics, the equation can be used to create specific shapes and patterns.
Overall, the equation of a circle through the points of intersection of two circles and those of a circle and a straight line is a mathematical concept that can be used in many different contexts and applications.
How is Required Equation of a circle through the points of intersection of two circles and Those of a circle and A straight line
To find the equation of a circle passing through the points of intersection of two circles and those of a circle and a straight line, follow these steps:
- Find the points of intersection of the two given circles. Let these points be denoted by (x1, y1) and (x2, y2).
- Find the points of intersection of the given circle and the straight line. Let these points be denoted by (x3, y3) and (x4, y4).
- Use the formula for the distance between two points to find the distance between (x1, y1) and (x2, y2). Let this distance be denoted by d1.
- Use the formula for the distance between two points to find the distance between (x3, y3) and (x4, y4). Let this distance be denoted by d2.
- Find the midpoint of the line segment connecting (x1, y1) and (x2, y2), and the midpoint of the line segment connecting (x3, y3) and (x4, y4). Let these midpoints be denoted by (x5, y5) and (x6, y6), respectively.
- Find the slope of the line passing through (x5, y5) and (x6, y6). Let this slope be denoted by m.
- Use the formula to find the coordinates of the center of the circle, which is the point of intersection of the two lines passing through (x5, y5) with slope m and the point (x3, y3) with slope perpendicular to m. Let these coordinates be denoted by (h, k).
- Use the formula to find the radius of the circle, which is equal to half the distance between (h, k) and any of the intersection points, such as (x1, y1) or (x2, y2).
Once you have found the center (h, k) and radius r of the circle, you can write the equation in the standard form:
(x – h)^2 + (y – k)^2 = r^2
This is the equation of the circle passing through the points of intersection of the two given circles and those of the given circle and the straight line.
Case Study on Equation of a circle through the points of intersection of two circles and Those of a circle and A straight line
One possible case study involving the equation of a circle through the points of intersection of two circles and those of a circle and a straight line could be the design of a circular intersection or roundabout in a road network.
A circular intersection is a type of intersection in which traffic flows around a central island in a circular pattern, and vehicles entering or exiting the intersection yield to the traffic already in the circle. These types of intersections can improve traffic flow and reduce the occurrence of severe crashes compared to traditional intersections with traffic signals or stop signs.
To design a circular intersection, engineers need to determine the optimal size and position of the central island and the radius of the circular roadway. One approach is to use the equation of a circle through the points of intersection of two circles and those of a circle and a straight line to find the center and radius of the circle that will form the circular roadway.
Suppose we have two roads intersecting at a right angle, and we want to design a circular intersection to improve traffic flow. We can use the following steps to find the equation of the circle passing through the points of intersection of the two roads and the center of the intersection:
- Find the points of intersection of the two roads. Let these points be denoted by (x1, y1) and (x2, y2).
- Find the midpoint of the line segment connecting (x1, y1) and (x2, y2). Let this midpoint be denoted by (x3, y3).
- Draw a circle passing through (x1, y1) and (x2, y2) with center at (x3, y3). Let the radius of this circle be denoted by r1.
- Draw a line passing through (x1, y1) and (x2, y2) and find its perpendicular bisector. Let this line be denoted by L1.
- Find the points of intersection of L1 and each of the two roads. Let these points be denoted by (x4, y4) and (x5, y5).
- Find the midpoint of the line segment connecting (x4, y4) and (x5, y5). Let this midpoint be denoted by (x6, y6).
- Draw a circle passing through (x4, y4), (x5, y5), and (x6, y6). Let the radius of this circle be denoted by r2.
- Find the intersection point of the two circles with radii r1 and r2. Let this point be denoted by (h, k).
- The center of the circular intersection is (h, k) and the radius is r1 + r2.
Using this approach, engineers can design circular intersections that are tailored to the specific needs and characteristics of the road network, and that provide improved safety and efficiency for drivers and pedestrians.
White paper on Equation of a circle through the points of intersection of two circles and Those of a circle and A straight line
Title: Design of Circular Intersections using Equations of Circles and Lines
Abstract:
Circular intersections, also known as roundabouts, are a common type of intersection used in transportation engineering to improve traffic flow and reduce the frequency and severity of crashes. In this paper, we present a method for designing circular intersections using equations of circles and lines. Specifically, we demonstrate how to find the equation of a circle passing through the points of intersection of two circles and those of a circle and a straight line. We then illustrate how this equation can be used to determine the optimal size and position of a circular roadway in a circular intersection. We provide examples and practical applications of this method, and discuss the benefits and limitations of circular intersections compared to traditional intersections.
Introduction:
Circular intersections are a type of intersection in which traffic flows around a central island in a circular pattern, and vehicles entering or exiting the intersection yield to the traffic already in the circle. These types of intersections can improve traffic flow and reduce the occurrence of severe crashes compared to traditional intersections with traffic signals or stop signs. However, designing a circular intersection requires careful consideration of various factors, including traffic volume, vehicle speeds, pedestrian and bicycle access, and geometric constraints of the roadway network. In this paper, we present a method for designing circular intersections using equations of circles and lines.
Methodology:
We begin by considering a scenario in which two roads intersect at a right angle. We then follow the steps outlined in the previous case study to find the equation of a circle passing through the points of intersection of the two roads and the center of the intersection. This equation can be written in standard form as:
(x – h)^2 + (y – k)^2 = (r1 + r2)^2
where (h, k) is the center of the circular intersection, r1 is the radius of the circle passing through the points of intersection of the two roads, and r2 is the radius of the circle passing through the points of intersection of the straight line and the two roads.
To find the values of h, k, and r1 + r2, we can solve the system of equations formed by the equations of the two circles and the equation of the perpendicular bisector of the straight line. This system can be solved using algebraic or geometric methods, and the resulting values can be used to determine the size and position of the circular roadway in the intersection.
Results:
Using this method, engineers can design circular intersections that are tailored to the specific needs and characteristics of the road network. For example, if the roads have high traffic volumes and speeds, a larger circle with a higher speed limit may be appropriate. If the roads have lower volumes and speeds, a smaller circle with slower speeds may be more appropriate. The method can also be used to optimize the location of pedestrian and bicycle crossings, and to ensure adequate turning radii for various types of vehicles.
Conclusion:
Circular intersections are a useful tool for improving traffic flow and safety in transportation engineering. By using equations of circles and lines to design circular intersections, engineers can ensure that the intersections are optimized for the specific needs and characteristics of the road network. However, it is important to consider the limitations of circular intersections, such as increased driver confusion and reduced capacity for high volumes of left-turning traffic. Overall, the use of equations of circles and lines provides a valuable tool for designing circular intersections that are safe, efficient, and effective.