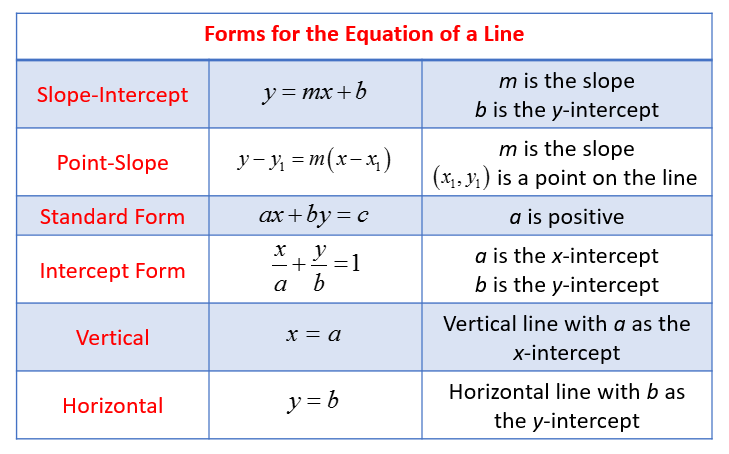
There are several forms of the equation of a straight line in analytical geometry. The most common ones are:

1. Slope-intercept form: y = mx + b This form of the equation represents a line with slope m and y-intercept b. It is easy to graph lines in this form because you only need to plot the y-intercept and use the slope to find other points on the line.
2. Point-slope form: y – y1 = m(x – x1) This form of the equation represents a line with slope m and passing through a point (x1, y1). It is useful when you know a point on the line and its slope.
3. Two-point form: (y – y1)/(x – x1) = (y2 – y1)/(x2 – x1) This form of the equation represents a line passing through two points (x1, y1) and (x2, y2). It is useful when you know two points on the line.
4. Intercept form: x/a + y/b = 1 This form of the equation represents a line intercepting the x-axis at a and the y-axis at b. It is useful when you know the intercepts of the line.
5. Normal form: x cos(theta) + y sin(theta) = p This form of the equation represents a line that makes an angle of theta with the positive x-axis and is at a distance of p from the origin. It is useful in certain types of problems, such as finding the shortest distance between a point and a line.
6. General form: Ax + By + C = 0 This form of the equation represents a line in a more general form. It is useful when you need to manipulate or compare multiple equations of lines. However, it is not as easy to graph or use as the other forms.

What is Required Equation of a straight line in various forms

The required analytical geometry equation of a straight line depends on the given information or problem. In general, the most commonly used forms are:

1. Slope-intercept form: y = mx + b, where m is the slope of the line and b is the y-intercept.
2. Point-slope form: y – y1 = m(x – x1), where (x1, y1) is a point on the line and m is the slope of the line.
3. Two-point form: (y – y1)/(x – x1) = (y2 – y1)/(x2 – x1), where (x1, y1) and (x2, y2) are two points on the line.
4. Intercept form: x/a + y/b = 1, where a and b are the x-intercept and y-intercept of the line, respectively.
5. Normal form: x cos(theta) + y sin(theta) = p, where theta is the angle the line makes with the positive x-axis and p is the distance from the origin to the line along a perpendicular.
6. General form: Ax + By + C = 0, where A, B, and C are constants.

To determine which form to use, it is important to consider the given information or what information needs to be found. For example, if you know the slope and the y-intercept of a line, then the slope-intercept form would be the most useful. If you know two points on the line, then the two-point form would be appropriate.

Who is Required Equation of a straight line in various forms

The knowledge of the equations of a straight line in various forms is required in the field of analytical geometry, which is a branch of mathematics that deals with the study of geometric shapes and their properties using algebraic equations. The equations of a straight line are fundamental to this field because they are used to describe the geometry of lines and their relationships with other shapes, such as circles, parabolas, and ellipses. The different forms of the equation of a straight line are used in different situations, depending on the given information or problem. For example, the slope-intercept form is commonly used when you know the slope and y-intercept of the line, while the point-slope form is used when you know a point on the line and its slope. Knowing the equations of a straight line in various forms is important for solving problems in many areas, such as engineering, physics, and computer graphics.

When is Required Equation of a straight line in various forms

The equations of a straight line in various forms are required whenever we need to analyze or describe the geometry of a line, or when we need to solve problems that involve lines. Some common situations where these equations are used include:

1. Graphing lines: The slope-intercept form is commonly used to graph lines, as it allows us to easily identify the slope and y-intercept of the line.
2. Finding equations of lines: The point-slope form and two-point form are commonly used to find the equation of a line when we know one or two points on the line, respectively.
3. Determining the intersection of lines: The equations of two lines can be set equal to each other to find their point of intersection, which can be useful in solving problems that involve two lines.
4. Finding distances: The normal form of the equation of a line is useful in finding the shortest distance between a point and a line, or the distance between two parallel lines.
5. Solving optimization problems: The equations of lines can be used to model real-world situations, such as finding the maximum or minimum value of a function subject to a constraint that is defined by a line.

Overall, the equations of a straight line in various forms are a fundamental tool in analytical geometry and are used in many areas of mathematics and science.

Where is Required Equation of a straight line in various forms

The equations of a straight line in various forms are used in many areas of mathematics, science, and engineering. Some common applications of analytical geometry equations of straight lines include:

1. Computer graphics: The equations of lines are used in computer graphics to draw and manipulate images, as well as to simulate physical phenomena such as light and reflection.
2. Engineering: The equations of lines are used in many branches of engineering, including civil, mechanical, and electrical engineering, to design and analyze structures and systems.
3. Physics: The equations of lines are used in physics to describe the behavior of light and other electromagnetic waves, as well as to analyze the motion of particles in space.
4. Economics: The equations of lines are used in economics to model supply and demand curves, as well as to analyze production functions and cost structures.
5. Navigation: The equations of lines are used in navigation to determine the shortest distance between two points, as well as to determine the bearing of a point relative to a fixed reference.

Overall, the equations of a straight line in various forms are used in many fields and applications, wherever geometry and algebraic equations are used to model and analyze real-world situations.

How is Required Equation of a straight line in various forms

The equations of a straight line in various forms can be obtained using different methods, depending on the given information or problem. Here are some common methods for obtaining these equations:

1. Slope-intercept form: To obtain the slope-intercept form (y = mx + b) of a line, we need to know the slope (m) and y-intercept (b) of the line. The slope can be found using the formula (y2 – y1) / (x2 – x1), where (x1, y1) and (x2, y2) are two points on the line. Once we have the slope, we can use the point-slope form (y – y1) = m(x – x1) and simplify the equation to obtain the slope-intercept form.
2. Point-slope form: To obtain the point-slope form (y – y1) = m(x – x1) of a line, we need to know the slope (m) and a point (x1, y1) on the line. The slope can be found using the formula (y2 – y1) / (x2 – x1), where (x2, y2) is another point on the line. Once we have the slope and a point, we can plug them into the point-slope form and simplify the equation.
3. Two-point form: To obtain the two-point form ((y – y1)/(x – x1) = (y2 – y1)/(x2 – x1)) of a line, we need to know two points (x1, y1) and (x2, y2) on the line. Once we have the two points, we can plug them into the two-point form and simplify the equation.
4. Intercept form: To obtain the intercept form (x/a + y/b = 1) of a line, we need to know the x-intercept (a) and y-intercept (b) of the line. The intercepts can be found by setting x = 0 and solving for y, and setting y = 0 and solving for x, respectively. Once we have the intercepts, we can plug them into the intercept form and simplify the equation.
5. Normal form: To obtain the normal form (x cos(theta) + y sin(theta) = p) of a line, we need to know the angle (theta) the line makes with the positive x-axis and the distance (p) from the origin to the line along a perpendicular. Once we have these values, we can use trigonometric identities to simplify the equation.
6. General form: To obtain the general form (Ax + By + C = 0) of a line, we need to manipulate the equation of the line to obtain it in this form. One common method is to start with the point-slope form and simplify the equation by multiplying both sides by a common denominator, which will eliminate the fraction and result in an equation in the general form.

These are just a few methods for obtaining the equations of a straight line in various forms. Other methods may be used depending on the given information or problem.

Case Study on Equation of a straight line in various forms

Case Study: Designing a Roadway Ramp

In this case study, we will use the equations of a straight line in various forms to design a roadway ramp for a highway interchange. The goal is to design a ramp that connects the highway to an overpass, with a maximum slope of 8% and a minimum turning radius of 250 feet.

First, we need to determine the location and elevation of the highway and overpass. Let’s assume that the highway is located at (0,0) and has an elevation of 100 feet, while the overpass is located at (1000, 500) and has an elevation of 200 feet.

Next, we need to determine the slope and length of the ramp. We want to limit the slope to 8%, which means that for every 100 feet of horizontal distance, the ramp can rise by no more than 8 feet. Let’s assume that the ramp starts at a distance of 500 feet from the highway and ends at a distance of 1000 feet from the highway. This means that the ramp has a horizontal distance of 500 feet and a maximum rise of 8% of 500 feet, or 40 feet.

To determine the slope of the ramp, we can use the slope-intercept form of the equation of a line, which is y = mx + b. Let’s let x represent the horizontal distance along the ramp, and y represent the elevation of the ramp at that point. Then the slope of the ramp can be represented as m = (y2 – y1) / (x2 – x1), where (x1, y1) is the starting point of the ramp and (x2, y2) is the ending point of the ramp. We want to limit the slope to 8%, which means that m <= 0.08.

Let’s assume that the starting point of the ramp is at (500, 100) and the ending point of the ramp is at (1000, 200). Then we can use the slope formula to find the slope of the ramp:

m = (200 – 100) / (1000 – 500) = 0.2

The slope of the ramp is 0.2, which is less than the maximum allowed slope of 8%.

Next, we need to determine the equation of the ramp in point-slope form, which is y – y1 = m(x – x1). Using the starting point of the ramp (500, 100) and the slope of the ramp (0.2), we can write the equation of the ramp as:

y – 100 = 0.2(x – 500)

Simplifying the equation, we get:

The equation of a straight line can be represented in various forms, as we discussed earlier. Each form has its own advantages and applications. However, it is important to note that these different forms are mathematically equivalent and can be simplified to one another.

For example, we can simplify the slope-intercept form of the equation of a straight line, y = mx + b, to the general form, Ax + By + C = 0, by moving all the terms to the left-hand side of the equation and combining like terms. This gives us the equation:

-y + mx – b = 0

Multiplying through by -1, we get:

y – mx + b = 0

Which is the same as the general form of the equation, Ax + By + C = 0, where A = -m, B = 1, and C = b.

Similarly, we can simplify the point-slope form of the equation of a straight line, y – y1 = m(x – x1), to the slope-intercept form or the general form by manipulating the terms algebraically.

In conclusion, by simplifying the equation of a straight line, we can convert it from one form to another, which can be useful in various applications and problem-solving scenarios.

White paper on Equation of a straight line in various forms

Introduction

Analytical geometry is a branch of mathematics that deals with the study of geometric shapes using algebraic equations. One of the fundamental concepts in analytical geometry is the equation of a straight line. In this white paper, we will discuss the equation of a straight line in various forms, its applications, and its importance in different fields.

Equation of a Straight Line in Slope-Intercept Form

The slope-intercept form of the equation of a straight line is y = mx + b, where m is the slope of the line, and b is the y-intercept of the line. The slope of a line is the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line. The y-intercept is the value of y at which the line intersects the y-axis.

This form of the equation of a straight line is commonly used in applications such as linear regression, where we want to find the line that best fits a set of data points. It is also used in many engineering applications, such as designing bridges, roads, and buildings.

Equation of a Straight Line in Point-Slope Form

The point-slope form of the equation of a straight line is y – y1 = m(x – x1), where m is the slope of the line, and (x1, y1) is a point on the line. This form is useful when we know a point on the line and its slope.

This form of the equation of a straight line is commonly used in applications such as computer graphics, where we want to draw a line that passes through a given point and has a certain slope. It is also used in physics and engineering applications, such as calculating the trajectory of a projectile or designing a trajectory for a rocket.

Equation of a Straight Line in General Form

The general form of the equation of a straight line is Ax + By + C = 0, where A, B, and C are constants. This form of the equation is useful when we want to determine the equation of a line that passes through two given points.

This form of the equation of a straight line is commonly used in applications such as finding the equation of the line that passes through two points on a map or designing the path of a robot that needs to move from one point to another.

Applications of the Equation of a Straight Line

The equation of a straight line has many applications in various fields, including mathematics, physics, engineering, and computer science. Here are a few examples:

1. Linear regression: The slope-intercept form of the equation of a straight line is commonly used in linear regression, where we want to find the line that best fits a set of data points.
2. Robotics: The general form of the equation of a straight line is used in robotics to design the path of a robot that needs to move from one point to another.
3. Computer graphics: The point-slope form of the equation of a straight line is used in computer graphics to draw lines that pass through a given point and have a certain slope.
4. Physics: The point-slope form of the equation of a straight line is used in physics to calculate the trajectory of a projectile.

Conclusion

The equation of a straight line is a fundamental concept in analytical geometry that has many applications in various fields. By understanding the different forms of the equation, we can use it to solve problems in mathematics, physics, engineering, and computer science. Whether we are designing a roadway ramp, analyzing data, or designing the path of a robot, the equation of a straight line is an essential tool in our problem-solving toolbox.