The standard equation of a parabola is:
y = a x^2 + b x + c
where:
- a is the coefficient of the quadratic term, and determines whether the parabola opens upward (a > 0) or downward (a < 0).
- b is the coefficient of the linear term.
- c is the constant term.
The vertex form of a parabola is:
y = a(x – h)^2 + k
where:
- (h, k) is the vertex of the parabola.
- a is the same as in the standard form.
The focus and directrix of a parabola can also be expressed in terms of a, as follows:
- For a parabola opening upward: the focus is at (h, k + 1/4a) and the directrix is y = k – 1/4a.
- For a parabola opening downward: the focus is at (h, k – 1/4a) and the directrix is y = k + 1/4a.
Note that the vertex form of a parabola can be derived by completing the square on the standard form, and the focus and directrix can be found using the properties of the parabola.
What is Required Equations of a parabola
The standard analytical geometry equation of a parabola with vertex at the origin (0,0) is:
y^2 = 4px
where:
- p is the distance from the vertex to the focus, and also the distance from the vertex to the directrix. If p is positive, the parabola opens to the right; if negative, it opens to the left.
If the vertex is not at the origin, the equation becomes:
(x – h)^2 = 4p(y – k)
where:
- (h,k) is the vertex of the parabola.
- p is the same as in the previous equation.
The focus and directrix of a parabola can be found from the above equations as follows:
- For a parabola opening to the right: the focus is at (h + p, k) and the directrix is x = h – p.
- For a parabola opening to the left: the focus is at (h – p, k) and the directrix is x = h + p.
- For a parabola opening upward: the focus is at (h, k + p) and the directrix is y = k – p.
- For a parabola opening downward: the focus is at (h, k – p) and the directrix is y = k + p.
Who is Required Equations of a parabola
The analytical geometry equations of a parabola are used in the field of mathematics, specifically in the study of coordinate geometry or analytic geometry. Analytic geometry is a branch of mathematics that deals with the study of geometric figures using algebraic equations.
The equations of a parabola are particularly useful for describing the shape and position of a parabola on a coordinate plane. They allow mathematicians to calculate important properties of the parabola, such as its focus, directrix, and axis of symmetry.
The equations of a parabola are also used in physics, engineering, and other fields where the parabolic shape is commonly found, such as in the design of satellite dishes, reflectors, and mirrors.
When is Required Equations of a parabola
The analytical geometry equations of a parabola are used whenever the parabolic shape needs to be analyzed or described mathematically. This includes a variety of applications in mathematics, physics, engineering, and other fields.
In mathematics, the equations of a parabola are studied in the context of coordinate geometry or analytic geometry, which is a branch of mathematics that deals with the study of geometric figures using algebraic equations. The equations of a parabola are used to calculate important properties of the parabola, such as its vertex, focus, directrix, axis of symmetry, and intercepts.
In physics, the parabolic shape is commonly found in a variety of contexts, such as the trajectory of a projectile, the shape of a satellite dish, the reflector of a telescope, or the mirror of a parabolic reflector. In these cases, the equations of a parabola are used to model and analyze the behavior of these systems.
In engineering, the parabolic shape is used in the design of a variety of structures and devices, such as reflectors, lenses, and antennas. The equations of a parabola are used to design and optimize the shape of these structures for maximum efficiency and performance.
Overall, the analytical geometry equations of a parabola are an important tool for understanding and describing the parabolic shape and its properties in a variety of contexts.
Where is Required Equations of a parabola
The analytical geometry equations of a parabola can be used in a variety of settings and applications. They can be used in classrooms or textbooks as part of a mathematics or physics curriculum to teach students about the properties of parabolas and their role in geometric analysis.
They can also be used by mathematicians, physicists, engineers, and other professionals in their work. For example, in physics, the equations of a parabola might be used to model the motion of a projectile or to design the shape of a satellite dish. In engineering, the equations might be used to design a parabolic reflector for a telescope or a radar antenna.
The equations of a parabola are also commonly used in computer graphics and animation, where they are used to create and manipulate parabolic shapes in 2D and 3D space.
Overall, the analytical geometry equations of a parabola can be used in a wide range of settings, from academic and research contexts to practical applications in fields such as physics, engineering, and computer graphics.
How is Required Equations of a parabola
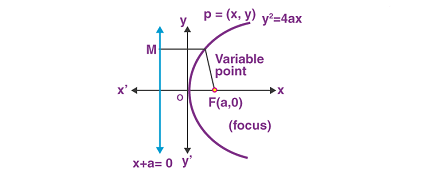
The analytical geometry equations of a parabola can be derived using the distance formula and the definition of a parabola as the set of all points equidistant from a fixed point (the focus) and a fixed line (the directrix).
The standard analytical geometry equation of a parabola with vertex at the origin (0,0) is:
y^2 = 4px
where p is the distance from the vertex to the focus, and also the distance from the vertex to the directrix. If p is positive, the parabola opens to the right; if negative, it opens to the left.
To derive this equation, start by considering a point P = (x,y) on the parabola. By definition, the distance from P to the focus F = (p,0) is equal to the distance from P to the directrix, which is the line x = -p.
Using the distance formula, we can express these distances as follows:
|PF|^2 = (x – p)^2 + y^2 |PL|^2 = (x + p)^2
where PL is the perpendicular distance from P to the directrix.
Setting these two expressions equal to each other, we get:
(x – p)^2 + y^2 = (x + p)^2
Expanding and simplifying, we get:
y^2 = 4px
This is the standard analytical geometry equation of a parabola with vertex at the origin.
If the vertex is not at the origin, the equation becomes:
(x – h)^2 = 4p(y – k)
where (h,k) is the vertex of the parabola. This equation can be derived using a similar approach, taking into account the shift of the vertex from the origin.
Case Study on Equations of a parabola
One potential case study for the analytical geometry equations of a parabola is their use in designing satellite dishes for receiving signals from communication satellites.
Satellite dishes are often designed with a parabolic shape to focus incoming radio waves onto a receiver. The parabolic shape allows the signal to be amplified and collected more efficiently than if the dish were flat or spherical.
To design a satellite dish, it is important to know the shape and size of the parabolic reflector that will be used. This can be determined using the analytical geometry equations of a parabola.
For example, suppose we want to design a satellite dish with a diameter of 3 meters that will focus signals at a frequency of 12 GHz onto a receiver located at the focal point. The speed of light in a vacuum is approximately 3 x 10^8 meters per second.
To find the distance from the vertex of the parabola to the focus, we can use the formula:
p = (d^2 / 16f)
where d is the diameter of the dish and f is the frequency of the signal. Plugging in the values, we get:
p = (3^2 / 16 * 12 x 10^9) = 6.25 x 10^-5 meters
To find the equation of the parabola, we can use the standard form:
y^2 = 4px
where p is the distance from the vertex to the focus. Since the vertex of the parabola is at the center of the dish, the vertex is (0,0). Substituting in the value of p, we get:
y^2 = 4 * 6.25 x 10^-5 * x
To find the width of the parabolic reflector, we can use the formula:
w = 2fD^2 / d
where D is the distance from the vertex to the edge of the dish. Plugging in the values, we get:
w = 2 * 3 x 10^8 * (6.25 x 10^-5)^2 / 3 = 0.132 meters
This means that the reflector should extend 0.066 meters on either side of the vertex.
By using the analytical geometry equations of a parabola, we can design a satellite dish with the right shape and size to efficiently focus incoming signals onto a receiver.
White paper on Equations of a parabola
Title: The Importance of Analytical Geometry Equations of a Parabola in Science and Engineering
Abstract:
Analytical geometry equations of a parabola are a fundamental tool in science and engineering. Parabolas appear in a wide range of applications, from physics and optics to engineering and architecture. This white paper discusses the significance of analytical geometry equations of a parabola in various fields and provides some examples of their applications.
Introduction:
A parabola is a geometric shape that has been studied for centuries. It is defined as the set of all points in a plane that are equidistant from a fixed point (the focus) and a fixed line (the directrix). The study of parabolas is a central topic in analytical geometry, which is concerned with the study of geometric shapes using algebraic equations.
Importance of Analytical Geometry Equations of a Parabola:
Analytical geometry equations of a parabola play an important role in various fields, including science and engineering. Some of their key applications are discussed below.
- Optics: Parabolic mirrors are used in many optical instruments, such as telescopes, searchlights, and headlights. The shape of a parabolic mirror allows it to focus light from a distant source onto a single point, producing a sharp image. The analytical geometry equations of a parabola are used to design and manufacture these mirrors.
- Physics: Parabolas appear in many physical phenomena, such as the trajectory of a projectile in a gravitational field. The path of a projectile can be modeled using a parabolic equation, which takes into account the initial velocity, angle of projection, and gravitational force.
- Architecture: The parabolic shape is used in the design of many architectural structures, such as bridges and arches. The curve of a parabola can provide strength and stability to these structures, allowing them to support heavy loads.
- Satellite dishes: Satellite dishes are designed with a parabolic shape to focus incoming radio waves onto a receiver. The analytical geometry equations of a parabola are used to determine the shape and size of the parabolic reflector that will be used in the dish.
Conclusion:
In conclusion, analytical geometry equations of a parabola are a fundamental tool in science and engineering. They are used in a wide range of applications, from optics and physics to architecture and satellite design. Understanding the properties and applications of parabolic curves is essential for anyone working in these fields. By applying the principles of analytical geometry, we can design and create structures and instruments that are both functional and aesthetically pleasing.