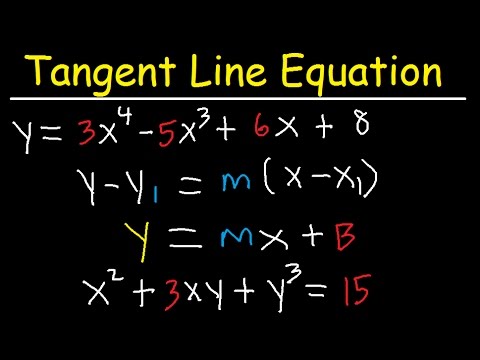
The equation of a tangent line to a curve at a specific point is given by:

y – y₁ = m(x – x₁)

where (x₁, y₁) is the point on the curve where the tangent line intersects the curve, and m is the slope of the tangent line at that point.

To find the slope of the tangent line, you can use the derivative of the function at that point:

m = f'(x₁)

where f'(x) is the derivative of the function f(x) with respect to x.

So, the equation of the tangent line to the curve y = f(x) at the point (x₁, y₁) is:

y – y₁ = f'(x₁)(x – x₁)

Tangent

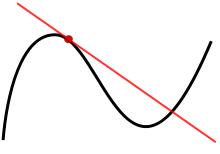
In calculation, the digression line (or basically digression) to a plane bend at a given point is the straight line that “simply contacts” the bend by then. Leibniz characterized it as the line through a couple of boundlessly close focuses on the bend. All the more exactly, a straight line is supposed to be a digression of a bend y = f(x) at a point x = c in the event that the line goes through the point (c, f(c)) on the bend and has slant f'(c), where f’ is the subordinate of f. A comparable definition applies to space endlessly bends in n-layered Euclidean space.
As it goes through where the digression line and the bend meet, called the place of juncture, the digression line is “heading down a similar path” as the bend, and is consequently the best straight-line estimate to the bend by then.

The digression line to a point on a differentiable bend can likewise be considered a digression line guess, the chart of the relative capability that best approximates the first capability at the given point.
Essentially, the digression plane to a surface at a given point is the plane that “simply contacts” the surface by then. The idea of a digression is quite possibly of the most principal thought in differential math and has been broadly summed up; see Digression space.

“Digression” comes from the Latin tangere, “to contact”.

Tangent line to a plane curve

The instinctive idea that a digression line “contacts” a bend can be made more unequivocal by thinking about the grouping of straight lines (secant lines) going through two focuses, An and B, those that lie on the capability bend. The digression at An is the cutoff when point B approximates or keeps an eye on A. The presence and uniqueness of the digression line relies upon a particular kind of numerical perfection, known as “differentiability.” For instance, on the off chance that two round circular segments meet at a sharp point (a vertex) there is no exceptionally characterized digression at the vertex on the grounds that the restriction of the movement of secant lines relies upon the heading in which “point B” moves toward the vertex.

At most places, the digression contacts the bend without crossing it (however it might, when proceeded, cross the bend at different places from the mark of digression). Where the digression (right now) crosses the bend is called an emphasis point. Circles, parabolas, hyperbolas and ovals have no enunciation point, however more muddled bends do have, similar to the diagram of a cubic capability, which has precisely one expression point, or a sinusoid, which has two intonation focuses per every time of the sine.

On the other hand, it might happen that the bend lies totally on one side of a straight line going through a point on it, but this straight line isn’t a digression line. This is the situation, for instance, for a line going through the vertex of a triangle and not converging it in any case — where the digression line doesn’t exist for the reasons made sense of above. In raised math, such lines are called supporting lines.

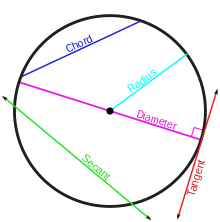
Tangent lines to circles

In Euclidean plane calculation, a digression line to a circle is a line that contacts the circle at precisely one point, never entering the circle’s inside. Digression lines to circles structure the subject of a few hypotheses, and assume a significant part in numerous mathematical developments and verifications. Since the digression line to a circle at a point P is opposite to the sweep to that point, hypotheses including digression lines frequently include outspread lines and symmetrical circles.

Law of tangents

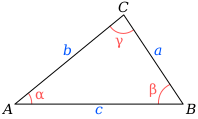
In geometry, the law of digressions is an assertion about the connection between the digressions of two points of a triangle and the lengths of the rival sides.

In Figure 1, a, b, and c are the lengths of the three sides of the triangle, and α, β, and γ are the points inverse those three particular sides. The law of digressions expresses that

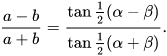
The law of digressions, albeit not so generally known as the law of sines or the law of cosines, is identical to the law of sines, and can be utilized regardless where different sides and the included point, or two points and a side, are known.

Tangent vector

In science, a digression vector is a vector that is digression to a bend or surface at a given point. Digression vectors are portrayed in the differential math of bends with regards to bends in Rn. All the more for the most part, digression vectors are components of a digression space of a differentiable complex. Digression vectors can likewise be portrayed with regards to microorganisms. Officially, a digression vector at the point x is a direct determination of the polynomial math characterized by the arrangement of microbes at x.

Case Study on Equations of tangent

Case Study:

Consider the equation of a tangent to the curve y = x^2 + 3x – 4 at the point where the tangent intersects the curve at x = 2.

Solution:

Step 1: Find the slope of the tangent at x = 2 To find the slope of the tangent at x = 2, we need to differentiate the equation of the curve with respect to x and evaluate it at x = 2.

y = x^2 + 3x – 4 dy/dx = 2x + 3 dy/dx at x = 2 = 2(2) + 3 = 7

So the slope of the tangent at x = 2 is 7.

Step 2: Find the y-coordinate of the point of tangency To find the y-coordinate of the point of tangency, we substitute x = 2 into the equation of the curve.

y = x^2 + 3x – 4 y at x = 2 = 2^2 + 3(2) – 4 = 6

So the point of tangency is (2, 6).

Step 3: Write the equation of the tangent Now we have the slope of the tangent and a point on the tangent. We can use point-slope form to write the equation of the tangent.

y – y1 = m(x – x1) y – 6 = 7(x – 2)

Simplifying, we get:

y = 7x – 8

So the equation of the tangent to the curve y = x^2 + 3x – 4 at the point where the tangent intersects the curve at x = 2 is y = 7x – 8.

Tangent space

In math, the digression space of a complex sums up to higher aspects the idea of digression planes to surfaces in three aspects and digression lines to bends in two aspects. With regards to physical science the digression space to a complex at a point can be seen as the space of potential speeds for a molecule continuing on the complex.