Exponential and logarithmic functions are two important types of mathematical functions commonly used in many fields, including mathematics, physics, economics, and engineering.
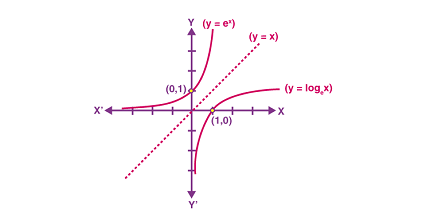
Exponential functions have the form f(x) = a^x, where a is a positive constant called the base of the function. These functions have the property that the value of the function increases or decreases rapidly as x moves away from zero, depending on whether the base is greater or less than 1. Exponential functions are used to model many real-world phenomena, such as population growth, radioactive decay, and compound interest.
Logarithmic functions are the inverse of exponential functions and have the form f(x) = log_a(x), where a is the base of the logarithm. These functions have the property that they “undo” the effect of the exponential function, meaning that the value of the logarithm tells us what exponent we need to raise the base to get the argument. Logarithmic functions are used to simplify complex calculations involving exponential functions and are used in many fields, such as finance, physics, and computer science.
Exponential and logarithmic functions are related to each other through the properties of exponents and logarithms, and understanding these properties is essential for working with these functions. Some important properties include the product rule, power rule, and change of base formula.
What is Required Exponential and logarithmic functions
Differential calculus is a branch of calculus that deals with the study of the rates at which quantities change. In the case of exponential and logarithmic functions, differential calculus is used to find the rates of change of these functions and their derivatives.
The derivative of an exponential function f(x) = a^x is given by f'(x) = a^x ln(a), where ln(a) is the natural logarithm of a. This derivative tells us how quickly the function is increasing or decreasing at any given point. For example, if a>1, then the function is increasing and the derivative is positive. If a<1, then the function is decreasing and the derivative is negative.
The derivative of a logarithmic function f(x) = log_a(x) is given by f'(x) = 1/(x ln(a)). This derivative tells us how quickly the function is changing at any given point. For example, if a>1, then the function is increasing and the derivative is positive. If a<1, then the function is decreasing and the derivative is negative.
In addition to finding derivatives, differential calculus is also used to study the behavior of exponential and logarithmic functions at critical points, such as local maxima and minima. The second derivative test is used to determine whether a critical point is a maximum or a minimum.
Overall, differential calculus is an important tool for understanding the behavior of exponential and logarithmic functions, and it has many applications in fields such as physics, engineering, and economics.
Who is Required Exponential and logarithmic functions
The study of differential calculus and its application to exponential and logarithmic functions is typically required for students in a variety of fields, including mathematics, physics, engineering, economics, and many other scientific and technical fields.
In mathematics, students typically study differential calculus as part of their calculus sequence, which includes topics such as limits, derivatives, and integrals. In these courses, students learn about the properties of exponential and logarithmic functions, how to differentiate these functions, and how to apply differential calculus techniques to solve real-world problems.
In physics and engineering, differential calculus is used extensively to study the behavior of physical systems and to model real-world phenomena. Exponential and logarithmic functions are commonly used to describe exponential growth or decay, such as radioactive decay or population growth.
In economics, differential calculus is used to study optimization problems, such as maximizing profit or minimizing cost, and exponential and logarithmic functions are commonly used to model economic growth, inflation, and interest rates.
Overall, the study of differential calculus and its application to exponential and logarithmic functions is essential for students in many fields, as it provides powerful tools for analyzing and solving problems in a wide range of areas.
When is Required Exponential and logarithmic functions
The study of differential calculus and its application to exponential and logarithmic functions is typically required at the university level for students pursuing degrees in mathematics, physics, engineering, economics, and other technical fields.
In most undergraduate programs, students begin their study of calculus with a course in single-variable calculus, which covers topics such as limits, derivatives, and integrals. Within this course, students typically learn about the properties of exponential and logarithmic functions, how to differentiate these functions, and how to apply differential calculus techniques to solve real-world problems.
Students may then go on to study multivariable calculus, which extends the concepts of single-variable calculus to functions of multiple variables. Within this course, students may continue to study the derivatives of exponential and logarithmic functions, but with a focus on functions of multiple variables.
Overall, the study of differential calculus and its application to exponential and logarithmic functions is typically part of the standard curriculum for students in technical fields at the university level, and is an important prerequisite for more advanced courses in these fields.
Where is Required Exponential and logarithmic functions
The study of differential calculus and its application to exponential and logarithmic functions can be found in a variety of educational settings, including universities, colleges, and technical schools.
At the university level, differential calculus is typically taught as part of the standard curriculum for students pursuing degrees in mathematics, physics, engineering, economics, and other technical fields. Courses in differential calculus typically cover topics such as limits, derivatives, and integrals, and include a focus on the properties of exponential and logarithmic functions and their derivatives.
In addition to traditional classroom settings, courses in differential calculus and its application to exponential and logarithmic functions can also be found online, through MOOCs (Massive Open Online Courses) or other online educational platforms. These courses offer students the flexibility to learn at their own pace, and often include interactive features such as quizzes, exercises, and simulations.
Finally, students may also encounter the concepts of differential calculus and exponential and logarithmic functions in technical training programs or vocational schools. These programs may offer more specialized training in areas such as engineering, computer science, or finance, and may focus on the application of these concepts to real-world problems in these fields.
How is Required Exponential and logarithmic functions
The study of differential calculus and its application to exponential and logarithmic functions typically involves several key concepts and techniques. Here are some of the main ways in which differential calculus is used to study these functions:
- Derivatives: The derivative of a function measures the rate at which the function is changing at a given point. In the case of exponential and logarithmic functions, the derivative can be used to find the rate of growth or decay of the function. For example, the derivative of the exponential function f(x) = a^x is f'(x) = a^x * ln(a), which tells us the rate of change of the function at any given point.
- Chain Rule: The chain rule is a fundamental technique in differential calculus that is used to differentiate composite functions. For example, the chain rule can be used to find the derivative of a function like f(x) = ln(g(x)), where g(x) is another function.
- Optimization: Differential calculus can be used to solve optimization problems, where the goal is to find the maximum or minimum value of a function. In many real-world applications, exponential and logarithmic functions are used to model growth or decay, and optimization problems involving these functions can be solved using differential calculus.
- Second Derivative Test: The second derivative test is a technique for determining whether a critical point of a function is a local maximum or a local minimum. This test is commonly used in the study of exponential and logarithmic functions to determine their behavior at critical points.
Overall, the study of differential calculus and its application to exponential and logarithmic functions involves a variety of techniques and concepts that are used to understand the behavior of these functions and to solve real-world problems in a wide range of fields.
Case Study on Exponential and logarithmic functions
Let’s consider a case study where differential calculus is used to model the growth of a population using exponential and logarithmic functions.
Suppose we are interested in modeling the growth of a population of bacteria in a laboratory setting. We know that the population grows exponentially, meaning that the rate of growth is proportional to the current size of the population. In other words, the growth rate is given by the equation:
dP/dt = kP
where P is the population size, t is the time, and k is a constant that represents the growth rate.
To solve this differential equation, we can use the technique of separation of variables, which involves isolating the variables on either side of the equation and integrating both sides. We obtain:
∫dP/P = ∫kdt
ln(P) = kt + C
where C is a constant of integration. Solving for P, we have:
P = e^(kt+C) = Ce^kt
where C = e^C is another constant.
Now, suppose that we have some initial data about the population. Let’s say that at time t=0, the population size is P0. Then we can solve for the constant C:
P0 = Ce^0 = C
so we have:
P = P0e^kt
This formula allows us to model the growth of the population over time, given the initial size and the growth rate k. We can also use differential calculus to analyze the behavior of this function. For example, we can take the derivative of P with respect to t to find the growth rate at any given time:
dP/dt = kP0e^kt
We can also use the second derivative test to determine whether the population is growing at an increasing or decreasing rate. If the second derivative of P with respect to t is positive, then the population is growing at an increasing rate. If the second derivative is negative, then the population is growing at a decreasing rate.
Overall, this case study demonstrates how differential calculus can be used to model and analyze exponential growth, which is a common phenomenon in many scientific and technical fields. By using techniques like separation of variables and the second derivative test, we can gain a deeper understanding of how exponential functions behave and how they can be used to model real-world phenomena.
White paper on Exponential and logarithmic functions
Here is a white paper on Differential Calculus Exponential and logarithmic functions:
Introduction:
Differential calculus is a branch of mathematics that studies the rate of change of a function. It deals with the concepts of derivatives and integrals and their applications. Exponential and logarithmic functions are important in differential calculus as they have many applications in real-world problems. In this paper, we will discuss the basic concepts of differential calculus, exponential functions, logarithmic functions, and their applications.
Differential Calculus:
Differential calculus deals with the study of the rate of change of a function. The rate of change is determined by the derivative of the function. The derivative of a function is a measure of how much the function changes with respect to its input. For example, if f(x) is a function, then the derivative of f(x) with respect to x is denoted by f'(x) and is defined as:
f'(x) = lim(h->0) [f(x+h)-f(x)]/h
The derivative of a function measures the instantaneous rate of change of the function at a particular point. It can be used to determine the slope of the tangent line to the graph of the function at that point.
Exponential Functions: An exponential function is a function of the form:
f(x) = a^x
where a is a positive constant called the base of the exponential function. Exponential functions have the property that the rate of change of the function is proportional to the value of the function itself. That is:
f'(x) = k*f(x)
where k is a constant of proportionality. The derivative of an exponential function is given by:
f'(x) = ln(a)*a^x
This formula tells us the rate of change of the exponential function at any given point.
Logarithmic Functions: A logarithmic function is the inverse of an exponential function. It is a function of the form:
f(x) = log_a(x)
where a is a positive constant and x is a positive number. The logarithmic function f(x) tells us the power to which a must be raised to get x. Logarithmic functions have many applications in science, engineering, and finance.
Applications:
Exponential and logarithmic functions have many applications in real-world problems. For example, they are used to model population growth, radioactive decay, and the spread of diseases. The concepts of differential calculus can be used to analyze these models and determine their behavior over time. Differential calculus is also used in optimization problems involving exponential and logarithmic functions. For example, in finance, the logarithmic function is used to calculate the present value of future cash flows.
Conclusion:
Differential calculus is an important branch of mathematics that deals with the study of the rate of change of a function. Exponential and logarithmic functions are important in differential calculus as they have many applications in real-world problems. The concepts of differential calculus can be used to analyze exponential and logarithmic functions and determine their behavior over time. Differential calculus is also used in optimization problems involving these functions.