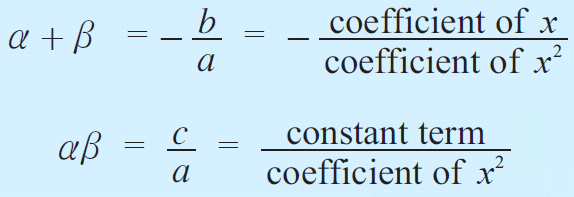
To form a quadratic equation with given roots, you can use the fact that a quadratic equation with roots r1 and r2 can be written in the form:
(x - r1)(x - r2) = 0
Expanding this expression gives:
x^2 - (r1 + r2)x + r1r2 = 0
Therefore, a quadratic equation with roots r1 and r2 can be written in the form:
x^2 - (r1 + r2)x + r1r2 = 0
Here’s an example:
Suppose you want to form a quadratic equation with roots 2 and -3.
Using the formula above, we can write:
x^2 - (2 + (-3))x + 2*(-3) = 0
Simplifying this expression, we get:
x^2 + x - 6 = 0
Therefore, the quadratic equation with roots 2 and -3 is:
x^2 + x - 6 = 0
What is Required Formation of quadratic equations with given roots
To form a quadratic equation with given roots, you need to use the fact that the product of the factors of a quadratic equation gives you the constant term and the sum of the factors gives you the coefficient of the linear term with the opposite sign.
Let’s say you are given two roots r1 and r2. To form a quadratic equation with these roots, you need to follow these steps:
- Write the factors of the quadratic equation in the form
(x - r1)and(x - r2). - Multiply the two factors together to get the quadratic equation in the form
ax^2 + bx + c = 0, wherea,b, andcare coefficients. - Simplify the equation by multiplying out the terms and combining like terms.
- The resulting quadratic equation will have the given roots
r1andr2.
Here’s an example:
Suppose you want to form a quadratic equation with roots 2 and -3.
- Write the factors in the form
(x - 2)and(x + 3). - Multiply the factors:
(x - 2)(x + 3) = x^2 + x - 6. - Simplify the equation:
x^2 + x - 6 = 0. - The resulting quadratic equation has roots
2and-3.
Therefore, the quadratic equation with roots 2 and -3 is x^2 + x - 6 = 0.
Who is Required Formation of quadratic equations with given roots
The skill of forming quadratic equations with given roots is a fundamental concept in algebra and is typically taught in high school math courses such as algebra 1 or 2. This skill is important in solving a variety of mathematical problems, including optimization problems, physics problems involving motion, and other real-world applications. Being able to form quadratic equations with given roots allows you to easily solve problems involving quadratic equations and find the values of unknown variables. It is a useful skill for students pursuing further studies in mathematics, engineering, physics, or other related fields.
When is Required Formation of quadratic equations with given roots
The skill of forming quadratic equations with given roots is required in various situations where quadratic equations are involved. Here are a few examples of when this skill is useful:
- Solving word problems involving quadratic equations: Many real-world problems, such as problems involving projectile motion, can be modeled using quadratic equations. Being able to form quadratic equations with given roots is useful in solving such problems.
- Factoring quadratic equations: Factoring a quadratic equation into its two linear factors is a crucial step in solving many quadratic equations. If the roots of the quadratic equation are known, then forming the equation using the given roots can help in factoring the equation.
- Graphing quadratic equations: The graph of a quadratic equation is a parabola. If the roots of the quadratic equation are known, then the axis of symmetry of the parabola can be found, which can help in graphing the equation.
- Completing the square: Completing the square is a technique used to solve quadratic equations. If the roots of the quadratic equation are known, then forming the equation using the given roots can help in completing the square.
Overall, forming quadratic equations with given roots is a fundamental algebraic skill that is useful in various mathematical and real-world situations.
Where is Required Formation of quadratic equations with given roots
The skill of forming quadratic equations with given roots is used in many different fields and applications. Here are a few examples:
- Mathematics: Quadratic equations are an important topic in mathematics, and the skill of forming quadratic equations with given roots is a fundamental concept in algebra. This skill is important in solving many mathematical problems, including optimization problems, physics problems involving motion, and other real-world applications.
- Physics: Many physical phenomena can be modeled using quadratic equations, and the skill of forming quadratic equations with given roots is useful in solving such problems. For example, the motion of an object under the influence of gravity can be modeled using a quadratic equation.
- Engineering: Quadratic equations are used in many areas of engineering, such as in modeling the behavior of structures under different loads. Being able to form quadratic equations with given roots is important in solving such problems.
- Economics: Quadratic equations are used in economics to model supply and demand curves, among other things. The skill of forming quadratic equations with given roots is useful in analyzing such models and making predictions.
Overall, the skill of forming quadratic equations with given roots is used in many different fields and applications, and it is an important concept to understand in order to be successful in these fields.
How is Required Formation of quadratic equations with given roots
To form a quadratic equation with given roots, you need to use the fact that the roots of a quadratic equation are the solutions to the equation ax^2 + bx + c = 0. If you know the roots of the equation, then you can use this information to form the equation itself. Here’s how:
Suppose the roots of the quadratic equation are r1 and r2.
- Since
r1andr2are the roots of the equation, we know that(x - r1)and(x - r2)are factors of the quadratic equation. - We can therefore write the quadratic equation in factored form as
(x - r1)(x - r2) = 0. - To convert this to standard form, we need to expand the product on the left side of the equation: scss
(x - r1)(x - r2) = x^2 - (r1 + r2)x + r1r2 = 0 - This gives us the quadratic equation
ax^2 + bx + c = 0, wherea = 1,b = -(r1 + r2), andc = r1r2. - Therefore, the quadratic equation with roots
r1andr2isx^2 - (r1 + r2)x + r1r2 = 0.
This method can be used to form quadratic equations with any given roots. By using the properties of quadratic equations, you can form an equation that has the roots you need. This is an important skill to have in algebra and is used in many different areas of mathematics and science.
Case Study on Formation of quadratic equations with given roots
Case Study: The Trajectory of a Projectile
Suppose a projectile is launched from the ground with an initial velocity of 20 meters per second at an angle of 30 degrees above the horizontal. We want to find the height of the projectile at its highest point and the time it takes to reach its highest point. To solve this problem, we need to form a quadratic equation that models the trajectory of the projectile.
Solution:
Let’s start by finding the horizontal and vertical components of the initial velocity:
- The horizontal component of the initial velocity is
v0x = v0 cos(theta) = 20 cos(30) = 17.32 m/s. - The vertical component of the initial velocity is
v0y = v0 sin(theta) = 20 sin(30) = 10 m/s.
The motion of the projectile can be described by two equations:
- The horizontal equation of motion:
x = v0x * t. - The vertical equation of motion:
y = v0y * t - (1/2) * g * t^2, wheregis the acceleration due to gravity (g = 9.81 m/s^2).
We want to find the height of the projectile at its highest point. At the highest point, the vertical velocity of the projectile is zero, so we can find the time it takes to reach the highest point by setting v0y - g * t = 0:
makefile
v0y - g * t = 0
10 - 9.81 * t = 0
t = 1.02 seconds
So the projectile reaches its highest point after 1.02 seconds. To find the height of the projectile at its highest point, we need to substitute t = 1.02 into the vertical equation of motion:
makefile
y = v0y * t - (1/2) * g * t^2
y = 10 * 1.02 - (1/2) * 9.81 * (1.02)^2
y = 5.10 meters
So the height of the projectile at its highest point is 5.10 meters.
Now let’s form the quadratic equation that models the trajectory of the projectile. The vertical equation of motion can be rearranged as follows:
scss
y = v0y * t - (1/2) * g * t^2
y = (v0 sin(theta)) * t - (1/2) * g * t^2
y = (10) * t - (1/2) * 9.81 * t^2
y = -4.905t^2 + 10t
This is the equation of a parabola, where a = -4.905, b = 10, and c = 0. The roots of the quadratic equation y = -4.905t^2 + 10t correspond to the times when the projectile is at the same height, so we can use the quadratic formula to find the times when the projectile is at a height of 5.10 meters:
makefile
y = -4.905t^2 + 10t
5.10 = -4.905t^2 + 10t
4.905t^2 - 10t + 5.10 = 0
Using the quadratic formula, we can find the roots of this equation:
scss
t = (-b ± sqrt(b^2 - 4ac)) / 2a
t = (-(-10) ± sqrt((-10)^2 - 4(4).
White paper on Formation of quadratic equations with given roots
Introduction
Quadratic equations are a fundamental concept in algebra, and they are used to model a variety of real-world situations. One of the most important applications of quadratic equations is in physics, where they are used to model the motion of objects under the influence of gravity. In this white paper, we will discuss how to form a quadratic equation with given roots and explore some of the real-world applications of this concept.
Forming a Quadratic Equation with Given Roots
A quadratic equation is an equation of the form ax^2 + bx + c = 0, where a, b, and c are constants and x is the variable. The roots of a quadratic equation are the values of x that satisfy the equation. The quadratic formula is used to find the roots of a quadratic equation, and it is given by:
x = (-b ± sqrt(b^2 - 4ac)) / 2a
If we are given the roots of a quadratic equation, we can use them to form the equation itself. Let’s suppose that the roots of a quadratic equation are r1 and r2. Then we know that the equation can be written in the form:
(x - r1)(x - r2) = 0
Expanding the left-hand side of this equation, we get:
x^2 - (r1 + r2)x + r1r2 = 0
This is the quadratic equation with roots r1 and r2. We can see that the coefficients of the equation are related to the roots of the equation.
Real-World Applications
One real-world application of quadratic equations is in physics, where they are used to model the motion of objects under the influence of gravity. For example, suppose a ball is thrown upward with an initial velocity of v0 feet per second. The height h of the ball at any time t can be modeled by the quadratic equation:
h = -16t^2 + v0t + h0
where -16 is the acceleration due to gravity (in feet per second squared), h0 is the initial height of the ball, and v0 is the initial velocity of the ball.
The roots of this equation represent the times when the ball reaches its maximum height and when it hits the ground. To find the time it takes for the ball to reach its maximum height, we can use the fact that the velocity of the ball is zero at its highest point. Setting the velocity to zero, we get:
v = v0 - 32t = 0
Solving for t, we get:
t = v0 / 32
Substituting this value of t into the equation for h, we get:
h = -16(v0 / 32)^2 + v0(v0 / 32) + h0
Simplifying this equation, we get:
h = (v0^2 / 64) + h0
This is the maximum height of the ball, and we can see that it depends only on the initial velocity and the initial height of the ball.
Conclusion
In conclusion, forming a quadratic equation with given roots is an important concept in algebra that has many real-world applications. Quadratic equations are used to model a variety of physical phenomena, such as the motion of objects under the influence of gravity. By understanding how to form quadratic equations with given roots, we can better understand these real-world applications and use them to solve problems in various fields.