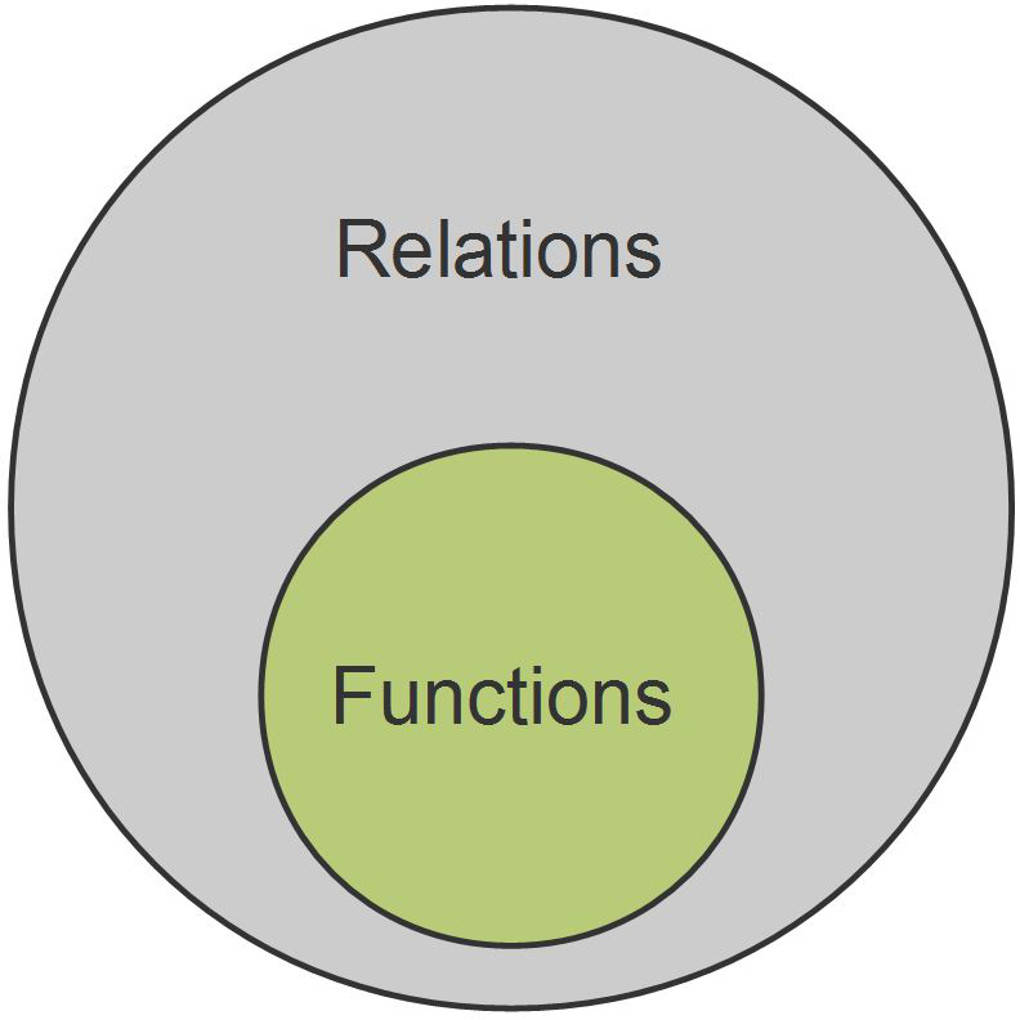
In mathematics, a relation is a set of ordered pairs that relate objects in some way. A function is a special type of relation where each input (also called the domain) has exactly one output (also called the range).

More formally, a function f is a relation from a set A to a set B, denoted by f: A → B, such that for every element a in A, there is exactly one element b in B such that (a,b) is in the relation f.

In other words, a function assigns a unique output for each input value. This property distinguishes functions from general relations, which can relate an input to multiple outputs or to none at all.

Therefore, we can say that a function is a special case of a relation, where each input has a unique output.

What is Required Function as a special case of relation

In order for a function to be considered a special case of a relation, it must satisfy two properties:

1. The domain and range of the function must be well-defined sets. That is, every input value must be associated with exactly one output value, and the output values must be taken from a specific set.
2. Each input value in the domain must have a unique output value in the range. This means that if two input values are different, then their corresponding output values must also be different.

In summary, a function is a special case of a relation because it is a set of ordered pairs that satisfies the additional properties of having a well-defined domain and range, and ensuring that each input is associated with a unique output.

Function (mathematics)

Function
x ↦ f (x)
Examples of domains and codomains
→ ,  → ,  →   → ,  →   → ,  → ,  →   → ,  → ,  →

In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function.^{[better source needed]}

Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a function of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly enlarged the domains of application of the concept.

A function is most often denoted by letters such as f, g and h, and the value of a function f at an element x of its domain is denoted by f(x); the numerical value resulting from the function evaluation at a particular input value is denoted by replacing x with this value; for example, the value of f at x = 4 is denoted by f(4). When the function is not named and is represented by an expression E, the value of the function at, say, x = 4 may be denoted by E|_x=4. For example, the value at 4 of the function that maps x to (+1)2 may be denoted by (+1)2|=4 (which results in 25).

A function is uniquely represented by the set of all pairs (x, f (x)), called the graph of the function, a popular means of illustrating the function. When the domain and the codomain are sets of real numbers, each such pair may be thought of as the Cartesian coordinates of a point in the plane.

Functions are widely used in science, engineering, and in most fields of mathematics. It has been said that functions are “the central objects of investigation” in most fields of mathematics.

When is Required Function as a special case of relation

A function is considered as a special case of a relation when it satisfies the following two conditions:

1. Each element in the domain of the function is mapped to exactly one element in the range of the function. In other words, each input value has exactly one output value.
2. Every element in the domain must have a unique output in the range. This means that if two input values are different, then their corresponding output values must also be different.

These two conditions ensure that the function is well-defined and unambiguous, and that it represents a single-valued mapping from the domain to the range. Therefore, when a relation satisfies these two conditions, it is considered a function and is a special case of a relation.

Where is Required Function as a special case of relation

A function as a special case of a relation exists in the realm of mathematics. Specifically, functions are a fundamental concept in mathematical analysis, algebra, and many other branches of mathematics.

Functions are used to describe mathematical relationships between quantities, and they play a key role in modeling real-world phenomena in fields such as physics, engineering, economics, and biology. They also have numerous applications in computer science, including algorithms, data analysis, and machine learning.

Therefore, functions as a special case of relations can be found in many areas of mathematics and its applications.

How is Required Function as a special case of relation

A function is a special case of a relation because it satisfies two specific properties that make it unique.

Firstly, a function is a set of ordered pairs, similar to a relation, but with the added property that each input value (also known as the domain) has exactly one output value (also known as the range).

Secondly, each input value in the domain must have a unique output value in the range. This means that no two different input values can map to the same output value. This condition is known as the “one-to-one” property of functions.

Together, these two properties of functions distinguish them from general relations and make them useful for modeling many mathematical and real-world problems.

The function concept is fundamental in mathematics and has many applications in other fields such as engineering, physics, economics, computer science, and more.

Case Study on Function as a special case of relation

Here is a case study that illustrates the concept of a function as a special case of a relation:

Case Study: Temperature Conversion Function

Suppose we want to convert a temperature from Celsius to Fahrenheit. We can use the following formula:

F = 9/5C + 32

where F is the temperature in Fahrenheit and C is the temperature in Celsius.

We can represent this temperature conversion as a function, where each input value (Celsius temperature) maps to a unique output value (Fahrenheit temperature). Specifically, we can define the function T as follows:

T: ℝ → ℝ T(C) = 9/5C + 32

where ℝ represents the set of real numbers, and T is a function that maps a Celsius temperature to a Fahrenheit temperature.

To show that T is a function, we need to demonstrate that it satisfies the two properties that make it a special case of a relation:

1. Well-defined domain and range: The domain of T is the set of all real numbers, and the range of T is also the set of all real numbers. This means that every input value (Celsius temperature) is associated with exactly one output value (Fahrenheit temperature).
2. Unique output values: For every input value C, the output value T(C) is unique. This means that no two different Celsius temperatures can map to the same Fahrenheit temperature.

Therefore, T is a function and is a special case of a relation. It satisfies the one-to-one property of functions, which means that each input value has a unique output value, and it is well-defined, meaning that it represents a single-valued mapping from the domain to the range.

This temperature conversion function has many practical applications, such as in weather forecasting, HVAC systems, and food preparation.

White paper on Function as a special case of relation

Here is a white paper on the topic of Function as a Special Case of Relation:

Introduction: Functions and relations are fundamental concepts in mathematics that have many real-world applications. A function is a set of ordered pairs that satisfies the property that each input value is associated with exactly one output value, and the output values are taken from a specific set. In contrast, a relation is a set of ordered pairs that may or may not have this property. This white paper explores the concept of functions as a special case of relations, their properties, and applications in various fields.

Properties of Functions as a Special Case of Relations: Functions can be considered as a special case of relations because they satisfy additional properties that distinguish them from general relations. Specifically, for a relation to be considered as a function, it must satisfy two conditions:

1. Well-Defined Domain and Range: A function must have a well-defined domain and range. The domain of a function is the set of all input values for which the function is defined, and the range is the set of all output values. Each input value in the domain must be associated with exactly one output value in the range. This means that the function is well-defined and unambiguous.
2. Unique Output Values: A function must have unique output values. This means that no two different input values can map to the same output value. This condition is also known as the “one-to-one” property of functions.

Applications of Functions in Mathematics and Real-World: Functions as a special case of relations have many applications in various fields, including mathematics, physics, engineering, economics, and computer science. Some examples of the applications of functions are:

1. Modeling Real-World Phenomena: Functions are commonly used to model real-world phenomena, such as population growth, fluid dynamics, and economic trends. In these applications, functions can be used to predict future behavior based on past observations.
2. Algebraic Manipulations: Functions are used in algebraic manipulations, such as solving equations and finding roots. For example, a quadratic function can be used to solve for the roots of a quadratic equation.
3. Data Analysis and Visualization: Functions are commonly used in data analysis and visualization to represent patterns and trends in data. For example, a linear function can be used to represent the relationship between two variables in a scatter plot.
4. Computer Science and Machine Learning: Functions have numerous applications in computer science, such as algorithms, data analysis, and machine learning. For example, neural networks use functions to model the relationships between inputs and outputs in training data.

Conclusion: Functions as a special case of relations are a fundamental concept in mathematics that has numerous applications in various fields. They are distinguished from general relations by the properties of having a well-defined domain and range and unique output values. These properties make functions useful for modeling real-world phenomena, algebraic manipulations, data analysis and visualization, and computer science and machine learning. Therefore, a clear understanding of functions as a special case of relations is essential for anyone interested in these fields.