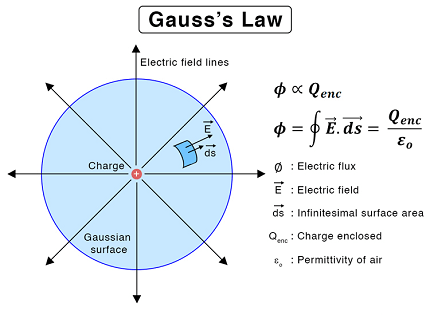
Gauss’s law is a fundamental law of electromagnetism that relates the distribution of electric charge to the resulting electric field. The law states that the electric flux through any closed surface is proportional to the total amount of electric charge enclosed within the surface.
In mathematical terms, Gauss’s law can be expressed as:
∮S E · dA = Q/ε₀
where ∮S represents the surface integral over a closed surface S, E is the electric field vector, dA is an infinitesimal element of surface area, Q is the total electric charge enclosed within the surface, and ε₀ is the electric constant (also known as the vacuum permittivity).
The law is named after the German mathematician and physicist Carl Friedrich Gauss, who formulated it in 1835. It is one of the four Maxwell’s equations that describe the behavior of electric and magnetic fields in space. Gauss’s law is a powerful tool for understanding the behavior of electric fields, and it is widely used in the analysis of electrical circuits, electromagnetic waves, and other phenomena in electromagnetism.
What is Required Gauss’s law
Gauss’s law requires a closed surface (often called a Gaussian surface) and a distribution of electric charge. The electric charge can be either positive or negative and can be distributed either continuously or discretely.
The Gaussian surface can be any closed surface that completely encloses the region of interest where the electric field is to be determined. The surface can be chosen to simplify the calculation of the electric field, as the electric flux through the surface is related to the electric charge enclosed within it.
Once the Gaussian surface is chosen, Gauss’s law states that the total electric flux through the surface is equal to the total electric charge enclosed within the surface divided by the electric constant ε₀. This means that the electric flux through a closed surface is proportional to the amount of charge inside it.
Gauss’s law is a fundamental principle of electromagnetism and is used in many areas of physics and engineering, including electric circuits, electrostatics, and electromagnetism. It is a powerful tool for understanding the behavior of electric fields, and it is often used in conjunction with other principles and equations to solve complex problems.
When is Required Gauss’s law
Gauss’s law is required when determining the electric field in situations where there is symmetry in the distribution of electric charge. The law is particularly useful in situations where the electric charge distribution has a high degree of symmetry, such as spherical, cylindrical, or planar symmetry.
When there is symmetry in the distribution of electric charge, Gauss’s law can be used to simplify the calculation of the electric field. This is because the electric flux through a closed surface can be related to the electric charge enclosed within the surface, and the electric field can be determined from the flux.
For example, if there is spherical symmetry in the distribution of electric charge, a spherical Gaussian surface can be chosen, and Gauss’s law can be applied to find the electric field at any point outside the sphere. Similarly, if there is cylindrical symmetry, a cylindrical Gaussian surface can be chosen, and Gauss’s law can be applied to find the electric field at any point outside the cylinder.
Overall, Gauss’s law is a powerful tool for determining the electric field in situations where there is symmetry in the distribution of electric charge, and it is widely used in many areas of physics and engineering.
Where is Required Gauss’s law
Gauss’s law is required in a wide range of applications in physics and engineering where the electric field needs to be determined. Some of the specific areas where Gauss’s law is commonly used include:
- Electrostatics: Gauss’s law is used to determine the electric field due to a charge distribution in a stationary (or electrostatic) scenario.
- Electrodynamics: Gauss’s law is used to analyze the behavior of time-varying electric fields and their interaction with magnetic fields.
- Electrical circuits: Gauss’s law is used to analyze the electric fields and potentials within circuits, including capacitors.
- Electromagnetic radiation: Gauss’s law is used to analyze the behavior of electromagnetic waves, including their propagation, reflection, and transmission.
- Plasma physics: Gauss’s law is used to understand the behavior of plasma, which is a gas-like state of matter composed of charged particles.
Overall, Gauss’s law is a fundamental principle of electromagnetism and is used in many different areas of physics and engineering to determine the electric field due to a distribution of electric charge.
How is Required Gauss’s law
Gauss’s law is a fundamental principle in electromagnetism that relates the electric flux through a closed surface to the electric charge enclosed within the surface. It is expressed mathematically as:
∮S E · dA = Q_enc / ε0
where ∮S is the surface integral over a closed surface S, E is the electric field at every point on the surface, dA is the differential area vector, Q_enc is the total electric charge enclosed within the surface, and ε0 is the electric constant (also known as the permittivity of free space).
This equation is known as the integral form of Gauss’s law, and it can be used to determine the electric field for certain symmetric charge distributions. However, for more complex charge distributions, it may be difficult to calculate the electric field using this integral form.
In such cases, Gauss’s law can be expressed in differential form as:
∇ · E = ρ / ε0
where ∇ is the divergence operator, E is the electric field, ρ is the charge density, and ε0 is the electric constant. This equation is known as the differential form of Gauss’s law, and it relates the electric field at every point in space to the charge density at that point.
The differential form of Gauss’s law is useful in solving problems involving non-symmetric charge distributions, as it allows for the calculation of the electric field at any point in space, given the charge density at that point.
Production of Gauss’s law
Gauss’s law is a fundamental principle in electromagnetism that relates the electric flux through a closed surface to the electric charge enclosed within the surface. The law was first formulated by the German mathematician and physicist Carl Friedrich Gauss in the early 19th century.
The basic idea behind Gauss’s law is that the total electric flux through a closed surface is proportional to the charge enclosed within the surface. This means that the electric field lines that pass through the surface must originate from or terminate at charges inside the surface.
To express this mathematically, Gauss used the concept of a flux integral, which is a mathematical tool for calculating the amount of flow of a vector field through a surface. In the case of electric flux, the vector field is the electric field, and the surface is a closed surface that encloses the charges of interest.
Gauss’s law can be stated mathematically as:
∮S E · dA = Q_enc / ε0
where ∮S is the surface integral over a closed surface S, E is the electric field at every point on the surface, dA is the differential area vector, Q_enc is the total electric charge enclosed within the surface, and ε0 is the electric constant (also known as the permittivity of free space).
This equation can be used to determine the electric field for certain symmetric charge distributions, and it is a powerful tool for solving problems in electromagnetism.
Case Study on Gauss’s law
A common application of Gauss’s law is in the calculation of the electric field for a charged conductor. Let’s consider a simple case study to illustrate this application:
Suppose we have a spherical conductor of radius R that is uniformly charged with a total charge Q. We want to find the electric field at any point outside the sphere.
To apply Gauss’s law, we first choose a Gaussian surface that encloses the entire sphere. A convenient choice for the surface is a concentric sphere of radius r > R.
By symmetry, we know that the electric field is radial and has the same magnitude at every point on the Gaussian surface. Therefore, we can simplify the integral in Gauss’s law as follows:
∮S E · dA = E ∮S dA = E 4πr^2
where E is the magnitude of the electric field and the surface integral simplifies to the area of the Gaussian sphere.
Next, we need to calculate the total charge enclosed within the Gaussian surface. Since the conductor is uniformly charged, we can express the charge density as:
ρ = Q / (4/3 π R^3)
and the total charge enclosed within the Gaussian surface is:
Q_enc = ρ (4/3 π r^3) = (Q R^3) / r^2
Substituting these expressions into Gauss’s law, we obtain:
E 4πr^2 = (Q R^3) / (ε0 r^2)
Solving for the electric field, we get:
E = (Q / (4π ε0 r^2)) (R^3 / r^3)
This result shows that the electric field outside the charged conductor decreases as the inverse square of the distance from the center of the sphere, just like the field of a point charge. It also depends on the total charge and size of the conductor.
This simple case study illustrates how Gauss’s law can be used to calculate the electric field for a charged conductor, and how the law can simplify calculations for symmetric charge distributions.
White paper on Gauss’s law
Introduction:
Gauss’s law is a fundamental principle in electromagnetism that relates the electric flux through a closed surface to the electric charge enclosed within the surface. It was first formulated by the German mathematician and physicist Carl Friedrich Gauss in the early 19th century. This white paper will explore the concept of Gauss’s law, its mathematical formulation, and its applications in physics and engineering.
Concept of Gauss’s law:
The basic idea behind Gauss’s law is that the total electric flux through a closed surface is proportional to the charge enclosed within the surface. This means that the electric field lines that pass through the surface must originate from or terminate at charges inside the surface.
The mathematical formulation of Gauss’s law:
To express this concept mathematically, Gauss used the concept of a flux integral, which is a mathematical tool for calculating the amount of flow of a vector field through a surface. In the case of electric flux, the vector field is the electric field, and the surface is a closed surface that encloses the charges of interest.
Gauss’s law can be stated mathematically as:
∮S E · dA = Q_enc / ε0
where ∮S is the surface integral over a closed surface S, E is the electric field at every point on the surface, dA is the differential area vector, Q_enc is the total electric charge enclosed within the surface, and ε0 is the electric constant (also known as the permittivity of free space).
Applications of Gauss’s law:
Gauss’s law has many applications in physics and engineering. One of its most important applications is in the calculation of the electric field for symmetric charge distributions. For example, if we have a charge distribution that is spherically symmetric, we can use Gauss’s law to calculate the electric field at any point outside the charge distribution.
Gauss’s law is also used in the design of capacitors, which are devices used to store electric charge. The capacitance of a capacitor depends on the geometry of its electrodes and the dielectric constant of the material between them. By applying Gauss’s law to a simple capacitor, we can derive an expression for its capacitance.
Another application of Gauss’s law is in the calculation of the electric flux density in a dielectric material. The electric flux density is a measure of the electric field strength per unit area of a material, and it depends on the electric field and the permittivity of the material. By applying Gauss’s law to a dielectric material, we can derive an expression for the electric flux density in terms of the charge density and the permittivity.
Conclusion:
In summary, Gauss’s law is a fundamental principle in electromagnetism that relates the electric flux through a closed surface to the electric charge enclosed within the surface. It provides a powerful tool for calculating the electric field for symmetric charge distributions, and has many applications in physics and engineering, including the design of capacitors and the calculation of the electric flux density in a dielectric material.