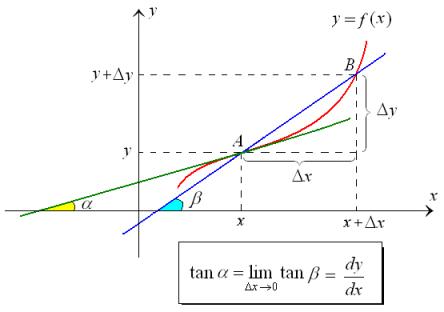
The derivative of a function can be interpreted geometrically in several ways. One common interpretation is that the derivative represents the slope of the tangent line to the graph of the function at a given point.
More specifically, if we consider a function f(x) and a point (a, f(a)) on its graph, the slope of the tangent line to the graph at that point is given by the derivative f'(a). The tangent line can be thought of as the line that just touches the graph at the point (a, f(a)) and has the same slope as the graph at that point.
Another geometric interpretation of the derivative is that it represents the rate of change of the function at a given point. For example, if we have a function that represents the position of an object over time, the derivative of the function at a particular time represents the instantaneous velocity of the object at that time.
Additionally, the derivative can be used to find the maximum and minimum points of a function. At a maximum or minimum point, the derivative of the function is zero, and the sign of the derivative changes from positive to negative (or vice versa).
Overall, the derivative of a function provides important geometric information about the behavior of the function at a given point, including its slope, rate of change, and extrema.
What is Required Differential Calculus Geometric interpretation of derivatives
Differential calculus is a branch of calculus that deals with the study of derivatives and their applications. The geometric interpretation of derivatives in differential calculus is essential in understanding the behavior of functions and their graphs.
The derivative of a function f(x) represents the slope of the tangent line to the graph of the function at a particular point. This slope indicates how fast the function is changing at that point. If the slope is positive, then the function is increasing; if it is negative, then the function is decreasing.
Geometrically, the derivative of a function can be interpreted as the rate at which the function changes at a particular point. For example, if we have a function that represents the position of an object over time, the derivative of the function at a particular time represents the instantaneous velocity of the object at that time. The sign of the derivative indicates the direction of motion, and the magnitude of the derivative indicates the speed.
The second derivative of a function gives us information about the curvature of the graph of the function. If the second derivative is positive, the graph is concave up, and if it is negative, the graph is concave down. A point where the second derivative is zero indicates an inflection point, where the curvature changes from concave up to concave down or vice versa.
In summary, the geometric interpretation of derivatives in differential calculus allows us to understand the behavior of functions and their graphs by providing information about their slopes, rates of change, velocities, and curvatures.
Who is Required Geometric interpretation of derivatives
The geometric interpretation of derivatives is an important concept in calculus and is required for anyone studying or applying calculus. This includes students in high school or college-level calculus courses, as well as professionals in fields such as physics, engineering, economics, and finance, who use calculus to solve problems related to rates of change, optimization, and modeling.
Understanding the geometric interpretation of derivatives allows individuals to better understand the behavior of functions and their graphs and provides insight into real-world applications of calculus. It is an essential concept for anyone working with calculus, whether in academia or in a professional setting.
When is Required Geometric interpretation of derivatives
The geometric interpretation of derivatives is required in a variety of situations where calculus is used. Here are some examples:
- In physics, the derivative of a position function gives the instantaneous velocity of an object at a particular time. The geometric interpretation of the derivative provides insight into the object’s motion, including its direction and speed.
- In economics, the derivative of a function represents the marginal rate of change of a variable with respect to another variable. The geometric interpretation of the derivative can provide insights into the behavior of markets, such as supply and demand curves.
- In engineering, the derivative is used to optimize designs, such as determining the maximum and minimum values of functions. The geometric interpretation of the derivative provides information about the shape of the function and the location of critical points.
- In finance, the derivative is used in options trading and risk management. The geometric interpretation of the derivative can help traders and risk managers understand the behavior of financial instruments and estimate their potential profits and losses.
Overall, the geometric interpretation of derivatives is required in any field where calculus is used to analyze rates of change, optimization, and modeling.
Where is Required Geometric interpretation of derivatives
The geometric interpretation of derivatives is required in many areas of mathematics, science, engineering, and finance. Here are some specific places where it is used:
- Calculus: The geometric interpretation of derivatives is fundamental to calculus, which is the branch of mathematics concerned with rates of change and their applications. Understanding the geometric interpretation of derivatives is essential for anyone studying or using calculus.
- Physics: The geometric interpretation of derivatives is used in physics to describe the motion of objects. For example, the derivative of a position function gives the velocity of an object at a particular time. The geometric interpretation of the derivative provides insight into the object’s motion, including its direction and speed.
- Engineering: The geometric interpretation of derivatives is used in engineering to optimize designs and determine the maximum and minimum values of functions. The geometric interpretation of the derivative provides information about the shape of the function and the location of critical points.
- Economics: The geometric interpretation of derivatives is used in economics to analyze supply and demand curves and determine optimal production levels. The derivative of a function represents the marginal rate of change of a variable with respect to another variable, and the geometric interpretation provides insight into the behavior of markets.
- Finance: The geometric interpretation of derivatives is used in finance to analyze financial instruments and estimate potential profits and losses. The derivative is used in options trading and risk management, and the geometric interpretation can help traders and risk managers understand the behavior of financial instruments.
Overall, the geometric interpretation of derivatives is used in many different fields and is a fundamental concept in mathematics and its applications.
How is Required Geometric interpretation of derivatives
The geometric interpretation of derivatives is used to understand the behavior of functions and their graphs. It provides insights into rates of change, velocities, and curvatures, among other things. Here are some ways in which the geometric interpretation of derivatives is used:
- Slope of tangent line: The derivative of a function gives the slope of the tangent line to the graph of the function at a particular point. This slope indicates how fast the function is changing at that point. The sign of the derivative indicates the direction of change (positive for increasing, negative for decreasing).
- Instantaneous velocity: In physics, the derivative of a position function gives the instantaneous velocity of an object at a particular time. The geometric interpretation of the derivative provides insight into the object’s motion, including its direction and speed.
- Curvature of graph: The second derivative of a function gives information about the curvature of the graph of the function. If the second derivative is positive, the graph is concave up, and if it is negative, the graph is concave down. A point where the second derivative is zero indicates an inflection point, where the curvature changes from concave up to concave down or vice versa.
- Optimization: In engineering and other fields, the derivative is used to optimize designs and determine the maximum and minimum values of functions. The geometric interpretation of the derivative provides information about the shape of the function and the location of critical points, which can be used to find optimal values.
- Marginal rate of change: In economics, the derivative of a function represents the marginal rate of change of a variable with respect to another variable. The geometric interpretation of the derivative provides insight into the behavior of markets, such as supply and demand curves.
Overall, the geometric interpretation of derivatives is a powerful tool that is used in many different fields to understand the behavior of functions and their graphs. It allows us to analyze rates of change, velocities, curvatures, and other important properties of functions.
Case Study on Geometric interpretation of derivatives
Let’s consider a case study where the geometric interpretation of derivatives is used to analyze the behavior of a function.
Case Study: Position Function and Instantaneous Velocity
Suppose we have a car moving along a straight line, and we want to analyze its motion using calculus. We can model the position of the car as a function of time, given by:
p(t) = t^3 – 3t^2 + 2t
We can use the derivative of this function to find the instantaneous velocity of the car at any particular time. The derivative of the position function is:
p'(t) = 3t^2 – 6t + 2
The geometric interpretation of this derivative is that it gives the slope of the tangent line to the graph of the position function at any point in time. The slope indicates how fast the car is moving at that moment, and the sign of the derivative indicates the direction of motion (positive for moving to the right, negative for moving to the left).
Suppose we want to find the instantaneous velocity of the car at time t = 1. We can evaluate the derivative at this point:
p'(1) = 3(1)^2 – 6(1) + 2 = -1
The negative sign indicates that the car is moving to the left, and the magnitude of the slope (1) indicates that the car is moving at a speed of 1 unit per second.
We can also use the second derivative of the position function to find information about the curvature of the graph. The second derivative is:
p”(t) = 6t – 6
If we evaluate this at t = 1, we get:
p”(1) = 6(1) – 6 = 0
This indicates that the graph of the position function has an inflection point at t = 1, where the curvature changes from concave up to concave down.
Overall, the geometric interpretation of derivatives allows us to analyze the motion of the car, including its position, velocity, and curvature. We can use the slope of the tangent line to find the instantaneous velocity, and the second derivative to find information about the curvature of the graph.
White paper on Geometric interpretation of derivatives
Here is a white paper on the Geometric Interpretation of Derivatives:
Introduction:
Derivatives are an important concept in calculus and are used in a wide range of fields, including mathematics, physics, engineering, economics, and more. One of the most important applications of derivatives is the geometric interpretation, which allows us to understand the behavior of functions and their graphs.
Geometric Interpretation:
The geometric interpretation of derivatives provides insights into the slopes, rates of change, velocities, and curvatures of functions and their graphs. Specifically, the derivative of a function represents the slope of the tangent line to the graph of the function at a particular point. This slope provides information about how fast the function is changing at that point, and the sign of the derivative indicates the direction of change (positive for increasing, negative for decreasing).
Instantaneous Velocity:
In physics, the derivative of a position function gives the instantaneous velocity of an object at a particular time. The geometric interpretation of the derivative provides insight into the object’s motion, including its direction and speed. For example, if we have a car moving along a straight line, we can model its position as a function of time and use the derivative of this function to find the instantaneous velocity of the car at any particular time.
Curvature:
The second derivative of a function gives information about the curvature of the graph of the function. If the second derivative is positive, the graph is concave up, and if it is negative, the graph is concave down. A point where the second derivative is zero indicates an inflection point, where the curvature changes from concave up to concave down or vice versa. The geometric interpretation of the second derivative provides insight into the shape of the graph and the location of critical points.
Optimization:
The derivative is used in engineering and other fields to optimize designs and determine the maximum and minimum values of functions. The geometric interpretation of the derivative provides information about the shape of the function and the location of critical points, which can be used to find optimal values.
Marginal Rate of Change:
In economics, the derivative of a function represents the marginal rate of change of a variable with respect to another variable. The geometric interpretation of the derivative provides insight into the behavior of markets, such as supply and demand curves.
Conclusion:
The geometric interpretation of derivatives is a powerful tool that is used in many different fields to understand the behavior of functions and their graphs. It allows us to analyze rates of change, velocities, curvatures, and other important properties of functions. The geometric interpretation provides insights into the motion of objects, the optimization of designs, and the behavior of markets.