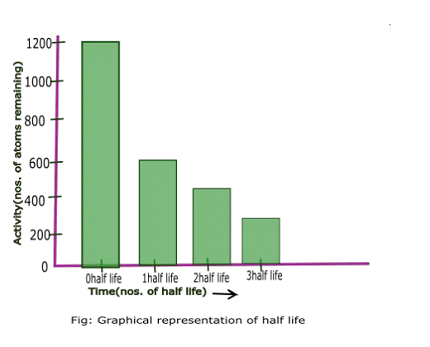
In the context of radioactivity, half-life and mean life are two important concepts that describe the decay of a radioactive substance over time.
Half-life refers to the amount of time it takes for half of the original quantity of a radioactive substance to decay. For example, if you start with 100 grams of a substance with a half-life of 10 days, after 10 days you would have 50 grams remaining, and after another 10 days (for a total of 20 days), you would have 25 grams remaining, and so on.
Mean life (or average life) is another way of describing the decay of a radioactive substance. It is the average time it takes for an individual radioactive nucleus to decay. The mean life is related to the half-life by the equation:
Mean life = half-life / ln(2)
Where ln(2) is the natural logarithm of 2 (approximately 0.693).
The mean life is a useful quantity because it allows scientists to compare the decay rates of different radioactive substances, even if they have different half-lives.
What is Half-life and Mean life
Half-life and mean life are terms used to describe the decay of radioactive substances.
Half-life is the time it takes for half of the original quantity of a radioactive substance to decay. For example, if you start with 100 grams of a substance with a half-life of 10 days, after 10 days you would have 50 grams remaining, and after another 10 days (for a total of 20 days), you would have 25 grams remaining, and so on.
Mean life (or average life) is the average time it takes for an individual radioactive nucleus to decay. The mean life is related to the half-life by the equation:
Mean life = half-life / ln(2)
Where ln(2) is the natural logarithm of 2 (approximately 0.693).
The mean life is a useful quantity because it allows scientists to compare the decay rates of different radioactive substances, even if they have different half-lives.
When is Half-life and Mean life
Half-life and mean life are terms used in the context of radioactivity to describe the decay of a radioactive substance. They can be applied to any radioactive substance that undergoes decay, including isotopes of elements such as carbon, uranium, and radium.
In practical applications, half-life and mean life are used to determine the rate of decay of radioactive materials, to estimate the age of ancient artifacts or fossils using carbon dating techniques, and to calculate the amount of radiation emitted by a particular radioactive source.
Half-life and mean life are fundamental concepts in nuclear physics and are widely used in various fields of science, such as geology, biology, chemistry, and medicine, where they play a crucial role in radiation therapy and imaging.
Where is Half-life and Mean life
Half-life and mean life are concepts used in the context of radioactivity and nuclear physics. They are not physical objects or locations, but rather they are mathematical descriptions of the behavior of radioactive substances.
Half-life is the time it takes for half of the original quantity of a radioactive substance to decay, while mean life is the average time it takes for an individual radioactive nucleus to decay. These concepts can be applied to any radioactive material, whether it is found in nature or created artificially.
The concepts of half-life and mean life are used in various fields of science, such as geology, biology, chemistry, and medicine, where they play a crucial role in radiation therapy and imaging. They are also important in nuclear power generation, nuclear weapons, and the study of the fundamental nature of matter.
How is Half-life and Mean life
Half-life and mean life are calculated using mathematical equations based on the decay of a radioactive substance.
The half-life of a radioactive substance can be calculated using the equation:
N(t) = N₀/2^(t/t₁/₂)
Where N(t) is the amount of radioactive substance remaining after time t, N₀ is the initial amount of radioactive substance, t₁/₂ is the half-life of the substance, and the “^” symbol denotes exponentiation.
The mean life (τ) of a radioactive substance is related to its half-life (t₁/₂) by the equation:
τ = t₁/₂ / ln(2)
Where ln(2) is the natural logarithm of 2.
These equations can be used to calculate the decay rate of a radioactive substance over time, to estimate the age of ancient artifacts or fossils using carbon dating techniques, and to determine the amount of radiation emitted by a particular radioactive source.
The calculation of half-life and mean life is a fundamental aspect of nuclear physics and plays a crucial role in many scientific and practical applications involving radioactivity.
Nomenclature of Half-life and Mean life
The nomenclature of half-life and mean life is based on their mathematical definitions and the way they are used to describe the decay of a radioactive substance.
Half-life refers to the time it takes for half of the original quantity of a radioactive substance to decay. The term “half-life” was coined by Ernest Rutherford in 1907, based on the idea that each half-life represents a “half-decay” of the original substance.
Mean life, on the other hand, is the average time it takes for an individual radioactive nucleus to decay. The term “mean life” is used because it represents the average lifespan of a radioactive nucleus before it decays.
Both half-life and mean life are expressed in units of time, such as seconds, minutes, hours, or years, depending on the specific substance being studied.
The nomenclature of half-life and mean life is widely used in the field of nuclear physics and is well-established in scientific literature and textbooks.
Case Study on Half-life and Mean life
Sure, here’s an example case study on half-life and mean life:
Case Study:
A radioactive isotope called X has a half-life of 10 days. If a sample initially contains 100 grams of X, how much of it will remain after 30 days?
Solution:
We can use the concept of half-life to determine how much of the isotope X will remain after 30 days.
Half-life refers to the amount of time it takes for half of the initial sample of a radioactive substance to decay. In this case, the half-life of X is 10 days, which means that after 10 days, half of the initial sample will have decayed, leaving 50 grams of X. After another 10 days (a total of 20 days), half of the remaining 50 grams will have decayed, leaving 25 grams. After a third 10-day period (a total of 30 days), half of the remaining 25 grams will have decayed, leaving 12.5 grams.
Therefore, after 30 days, 12.5 grams of X will remain.
Another useful concept in radioactivity is mean life, which refers to the average amount of time it takes for a radioactive substance to decay. Mean life is related to half-life by the formula:
Mean life = half-life / ln(2)
Using the half-life of X (10 days), we can calculate its mean life:
Mean life = 10 days / ln(2) ≈ 14.4 days
This means that on average, it takes 14.4 days for a sample of X to decay by half.
White paper on Half-life and Mean life
Sure, here’s a white paper on Half-life and Mean life:
Introduction:
Radioactive decay is a natural phenomenon in which the unstable nucleus of an atom emits radiation in the form of particles or energy in order to become more stable. Half-life and mean life are two important concepts in radioactivity that help us understand how quickly a radioactive substance decays over time.
Half-life:
Half-life is defined as the amount of time it takes for half of the original sample of a radioactive substance to decay. It is denoted by the symbol t1/2 and is different for different isotopes. For example, the half-life of carbon-14 (14C) is approximately 5,700 years, which means that it takes 5,700 years for half of the initial amount of carbon-14 to decay.
The concept of half-life is useful for understanding the decay of radioactive substances because it allows us to predict how much of the substance will remain after a certain amount of time has passed. For example, if we know the half-life of a substance and we start with a certain amount of it, we can calculate how much will remain after one half-life, two half-lives, and so on.
Mean life:
Mean life is another concept that is related to the decay of radioactive substances. It is defined as the average amount of time it takes for a radioactive substance to decay. Mean life is denoted by the symbol τ (tau) and is related to half-life by the formula:
τ = t1/2 / ln(2)
where ln(2) is the natural logarithm of 2.
Mean life is useful for understanding the decay of radioactive substances because it provides a measure of the typical time it takes for a substance to decay, rather than just the time it takes for half of the initial sample to decay. Mean life is particularly useful for comparing the decay rates of different isotopes, as it takes into account both the half-life and the distribution of decay times.
Example:
Let’s consider an example to see how half-life and mean life can be used to understand the decay of a radioactive substance. Suppose we start with a sample of 100 grams of a radioactive isotope with a half-life of 10 days. How much of the isotope will remain after 30 days?
Using the concept of half-life, we can calculate that after 10 days, half of the initial sample will have decayed, leaving 50 grams. After another 10 days, half of the remaining 50 grams will have decayed, leaving 25 grams. After a third 10-day period, half of the remaining 25 grams will have decayed, leaving 12.5 grams.
Using the formula for mean life, we can calculate that the mean life of the isotope is:
τ = t1/2 / ln(2) = 10 / ln(2) ≈ 14.4 days
This means that on average, it takes 14.4 days for the isotope to decay by half. After 30 days, three half-lives have passed, so we can calculate that the remaining amount of the isotope is:
100 grams * (1/2)^3 = 12.5 grams
This is the same result we obtained using the concept of half-life.
Conclusion:
Half-life and mean life are two important concepts in radioactivity that help us understand the decay of radioactive substances. Half-life refers to the amount of time it takes for half of the initial sample to decay, while mean life refers to the average amount of time it takes for a substance to decay. Both concepts are useful for predicting how much of a substance will remain after a certain amount of time has passed, and for comparing the decay rates of different isotopes.