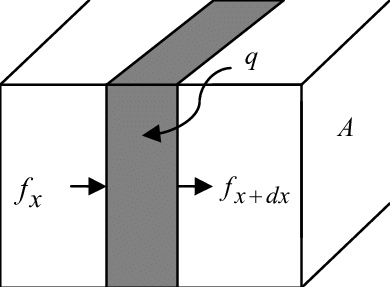
Heat conduction in one dimension is a process by which heat is transferred through a material in one direction only. The rate at which heat is conducted through the material is determined by the temperature gradient along the direction of heat flow, the thermal conductivity of the material, and the cross-sectional area perpendicular to the direction of heat flow.
The heat transfer equation for one-dimensional heat conduction is given by Fourier’s law:
q = -kA(dT/dx)
where q is the heat flux (heat transfer rate per unit area), k is the thermal conductivity of the material, A is the cross-sectional area of the material, and (dT/dx) is the temperature gradient (change in temperature per unit length) in the direction of heat flow.
The negative sign in the equation indicates that heat flows from a region of higher temperature to a region of lower temperature. The temperature gradient is proportional to the rate of heat transfer, and the thermal conductivity is a measure of how easily heat is conducted through the material.
Solving the heat conduction equation allows us to predict the temperature distribution within a material over time, given the initial temperature distribution and boundary conditions (such as the temperature at the ends of the material). This is an important tool in understanding and designing heat transfer systems, such as thermal insulation, heat exchangers, and electronic cooling systems.
What is Required Heat conduction in one dimension
Required heat conduction in one dimension refers to the amount of heat that needs to be conducted through a material to achieve a desired temperature distribution. This can be calculated using the heat conduction equation, which relates the heat flux (the rate of heat transfer per unit area) to the thermal conductivity of the material and the temperature gradient (the change in temperature per unit length).
To calculate the required heat conduction in one dimension, you first need to define the boundary conditions for the system, such as the temperature at the ends of the material. You also need to know the thermal conductivity of the material and the cross-sectional area perpendicular to the direction of heat flow.
Once you have these parameters, you can use the heat conduction equation to calculate the heat flux required to achieve the desired temperature distribution. This can then be used to determine the amount of heat that needs to be supplied to the material, or the rate at which heat needs to be removed from the material, to achieve the desired temperature distribution.
The calculation of required heat conduction is important in many engineering applications, such as the design of heat exchangers, electronic cooling systems, and thermal insulation. By understanding the heat transfer requirements of a system, engineers can design more efficient and effective heat transfer solutions.
Who is Required Heat conduction in one dimension
“Required Heat conduction in one dimension” is not a person, it is a technical concept related to heat transfer and thermodynamics. It refers to the amount of heat that needs to be conducted through a material in one direction to achieve a desired temperature distribution, and is calculated using the heat conduction equation. This concept is important in many fields, including engineering, physics, and materials science, as it allows engineers and scientists to design and analyze heat transfer systems, such as thermal insulation, heat exchangers, and electronic cooling systems.
When is Required Heat conduction in one dimension
“Required Heat conduction in one dimension” is a concept that is used whenever there is a need to understand or control heat transfer through a material in one direction. This can occur in a wide range of applications, including in thermal insulation, electronic cooling systems, and heat exchangers. For example, when designing a building, it is important to understand the required heat conduction in order to choose appropriate materials for insulation and heating/cooling systems. Similarly, in the design of electronic devices, it is important to control heat transfer to avoid overheating and damage to components. In general, any situation where heat needs to be transferred or controlled in one dimension can benefit from an understanding of required heat conduction.
Where is Required Heat conduction in one dimension
“Required Heat conduction in one dimension” is a concept that is applicable to any situation where heat needs to be transferred through a material in one direction. This can occur in a wide range of applications and locations, including in buildings, electronic devices, industrial equipment, and transportation systems. For example, in a building, required heat conduction is important for determining the thermal insulation needs of walls and windows. In electronic devices, it is important for designing cooling systems to prevent overheating of components. In industrial equipment, it can be used to optimize heat transfer in manufacturing processes. In transportation systems, it can be used to design heat management systems for engines and exhaust systems. In general, required heat conduction in one dimension is a concept that is relevant in many different locations and applications where heat transfer is an important consideration.
How is Required Heat conduction in one dimension
“Required Heat conduction in one dimension” can be calculated using the heat conduction equation, which relates the heat flux (the rate of heat transfer per unit area) to the thermal conductivity of the material and the temperature gradient (the change in temperature per unit length).
To calculate the required heat conduction in one dimension, one first needs to define the boundary conditions for the system, such as the temperature at the ends of the material. The thermal conductivity of the material and the cross-sectional area perpendicular to the direction of heat flow must also be known.
Once these parameters are defined, the heat conduction equation can be used to calculate the heat flux required to achieve the desired temperature distribution. This can then be used to determine the amount of heat that needs to be supplied to the material, or the rate at which heat needs to be removed from the material, to achieve the desired temperature distribution.
The calculation of required heat conduction in one dimension is important in many engineering applications, as it allows engineers to design and optimize heat transfer systems to meet specific thermal requirements. By understanding the heat transfer requirements of a system, engineers can design more efficient and effective heat transfer solutions, which can result in cost savings, improved performance, and increased reliability of systems.
Case Study on Heat conduction in one dimension
A common application of heat conduction in one dimension is in the design and optimization of building insulation. The amount of heat that flows through the walls, roof, and windows of a building can have a significant impact on energy consumption and comfort levels. Heat transfer through walls occurs in one dimension, and can be analyzed using the concepts of required heat conduction.
For example, consider a building with a wall made of a material with a known thermal conductivity and thickness. The temperature inside the building is kept at a constant level, and the outside temperature varies with the seasons. The amount of heat that flows through the wall is dependent on the temperature difference between the inside and outside, the thermal conductivity of the material, and the thickness of the wall. By calculating the required heat conduction in one dimension, engineers can determine the necessary thickness of insulation to achieve a desired level of thermal performance.
To perform this analysis, engineers first need to measure the thermal conductivity of the material and define the boundary conditions of the system, such as the inside and outside temperatures. They can then use the heat conduction equation to calculate the heat flux through the wall, and determine the thickness of insulation required to achieve a desired level of heat transfer resistance.
This calculation is important for optimizing the energy efficiency of buildings, as it allows engineers to design insulation systems that reduce the amount of heat that flows through walls, windows, and roofs. By optimizing insulation thickness and materials, engineers can reduce the energy required for heating and cooling, which can result in cost savings and a reduction in greenhouse gas emissions.
In summary, heat conduction in one dimension is an important concept in the design and optimization of building insulation, and is a common application of heat transfer principles in engineering.
White paper on Heat conduction in one dimension
White Paper: Understanding Heat Conduction in One Dimension
Introduction:
Heat transfer is a fundamental process that occurs in many natural and engineered systems. Understanding how heat is transferred through materials is essential for designing and optimizing systems that require heat transfer, such as in buildings, electronic devices, and industrial equipment. One important aspect of heat transfer is heat conduction, which refers to the transfer of heat through a material in one dimension. In this white paper, we will provide an overview of heat conduction in one dimension, including its definition, governing equation, and applications.
Definition:
Heat conduction in one dimension refers to the process by which heat is transferred through a material in one direction only, usually along the x-axis. This occurs when there is a temperature gradient along the direction of heat flow, with heat flowing from regions of high temperature to regions of low temperature. The rate of heat transfer is dependent on the thermal conductivity of the material, the temperature gradient, and the cross-sectional area perpendicular to the direction of heat flow.
Governing Equation:
Heat conduction in one dimension is governed by Fourier’s law, which states that the heat flux q (the rate of heat transfer per unit area) is proportional to the temperature gradient along the direction of heat flow. Mathematically, this is expressed as:
q = -k dT/dx
where k is the thermal conductivity of the material, T is the temperature, and x is the position along the direction of heat flow. The negative sign indicates that heat flows from regions of high temperature to regions of low temperature.
Applications:
Heat conduction in one dimension is an important concept in many fields, including engineering, physics, and materials science. It is used to analyze and design systems that require heat transfer, such as in building insulation, electronic cooling systems, and heat exchangers. By understanding the heat transfer properties of materials and systems, engineers can design more efficient and effective solutions that meet specific thermal requirements.
For example, in building insulation, understanding heat conduction in one dimension is critical for determining the necessary thickness and type of insulation required to achieve a desired level of thermal performance. By calculating the required heat conduction, engineers can determine the necessary thickness of insulation required to achieve a desired level of heat transfer resistance, which can reduce the amount of energy required for heating and cooling, resulting in cost savings and reduced greenhouse gas emissions.
Conclusion:
Heat conduction in one dimension is a fundamental concept in the study of heat transfer, with important applications in many fields, including engineering, physics, and materials science. By understanding the principles of heat conduction in one dimension, engineers can design and optimize systems that require heat transfer, resulting in more efficient and effective solutions that meet specific thermal requirements.