Huygen’s principle, named after the Dutch physicist Christiaan Huygens, is a fundamental principle in wave optics that explains how waves propagate through a medium.

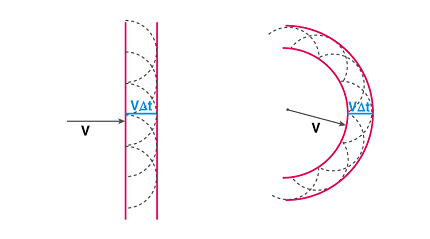
According to Huygen’s principle, each point on a wavefront can be considered as a source of secondary spherical waves. These secondary waves travel outwards from each point in all directions at the speed of the wave. The new wavefront at any given moment is formed by the constructive interference of all these secondary waves.

In other words, Huygen’s principle describes how waves propagate by continually creating new wavefronts through the interference of the secondary waves emanating from each point on the previous wavefront.

This principle is particularly useful for understanding phenomena such as diffraction and refraction, which are crucial in the study of optics, acoustics, and other branches of physics.

What is Required Huygen’s principle

Huygen’s principle is based on a few assumptions that are required for its application. These include:

1. The wavefront is a continuous surface, meaning that the wavefront does not have any breaks or abrupt changes.
2. The wave is propagating in a homogeneous medium, which means that the properties of the medium (such as its density or refractive index) are constant throughout.
3. The wave is a transverse wave, which means that the oscillations of the wave are perpendicular to the direction of propagation.
4. The size of the wavefront is much larger than the wavelength of the wave. This assumption is necessary to ensure that the wavefront can be approximated as a straight line.

When these assumptions are met, Huygen’s principle can be used to analyze the propagation of waves through a medium and to predict the behavior of waves when they encounter obstacles or pass through different media with different refractive indices.

When is Required Huygen’s principle

Huygen’s principle is required in many situations in which waves propagate through a medium, particularly in the field of wave optics. Some specific examples of when Huygen’s principle is useful include:

1. Diffraction: When a wave passes through a narrow aperture or encounters an obstacle, it diffracts, bending around the edges of the aperture or obstacle. Huygen’s principle can be used to predict the shape of the diffracted wavefront and the intensity of the diffracted waves.
2. Refraction: When a wave passes from one medium to another with a different refractive index, such as from air to water, it changes direction. Huygen’s principle can be used to predict the path of the refracted wave and the angle of refraction.
3. Reflection: When a wave reflects off a smooth surface, such as a mirror, it follows the law of reflection, which states that the angle of incidence equals the angle of reflection. Huygen’s principle can be used to explain why the reflected wavefront is smooth and coherent.
4. Interference: When two waves meet, they can interfere constructively or destructively, depending on the phase difference between them. Huygen’s principle can be used to predict the interference pattern that results from the interaction of two waves.

Overall, Huygen’s principle is a fundamental concept in the study of waves and is used extensively in fields such as optics, acoustics, and electromagnetism.

Where is Required Huygen’s principle

Huygen’s principle is required in a wide range of fields where waves propagate through a medium, including:

1. Optics: Huygen’s principle is essential in the study of light and its behavior as it propagates through various media, such as lenses, prisms, and diffraction gratings.
2. Acoustics: Huygen’s principle is used to study the behavior of sound waves as they travel through different media, such as air, water, and solids.
3. Electromagnetism: Huygen’s principle is used to study the behavior of electromagnetic waves, such as radio waves and microwaves, as they propagate through different media.
4. Seismology: Huygen’s principle is used to study the behavior of seismic waves as they propagate through the earth’s crust.
5. Fluid dynamics: Huygen’s principle is used to study the behavior of waves in fluids, such as water waves and ocean waves.

Overall, Huygen’s principle is a fundamental concept in the study of waves and is applied in a wide range of fields.

How is Required Huygen’s principle

Huygen’s principle can be used to explain how waves propagate through a medium and interact with other objects in their path. The principle can be applied in the following way:

1. Consider a wavefront that is propagating through a medium. Each point on the wavefront can be considered as a source of secondary waves that propagate outwards in all directions.
2. The secondary waves emanating from each point on the wavefront interfere constructively or destructively with each other. The interference pattern determines the shape of the new wavefront that is formed.
3. The new wavefront continues to propagate through the medium, and the process repeats at each point on the wavefront.
4. When the wave encounters an obstacle, such as an aperture or a reflecting surface, the secondary waves that emanate from each point on the wavefront interfere with each other to produce a diffraction or reflection pattern.
5. When the wave passes from one medium to another with a different refractive index, such as from air to water, the speed and direction of the wave change. Huygen’s principle can be used to predict the path of the refracted wave and the angle of refraction.

Overall, Huygen’s principle provides a powerful tool for understanding the behavior of waves in a variety of settings, and it is widely used in the study of optics, acoustics, and other fields of physics.

Nomenclature of Huygen’s principle

Huygen’s principle is named after the Dutch physicist Christiaan Huygens, who first proposed the principle in his book “Traité de la Lumière” (Treatise on Light) in 1678. The principle is sometimes also referred to as the Huygens-Fresnel principle, to acknowledge the contributions of French physicist Augustin-Jean Fresnel, who developed the principle further in the 19th century.

The nomenclature of Huygen’s principle can vary depending on the context in which it is being used. In optics, for example, the principle is often referred to as the wavefront principle or the wavelet principle, to emphasize the idea that each point on the wavefront acts as a source of secondary waves or wavelets that interfere to produce the overall wave pattern.

In other fields, such as acoustics or electromagnetism, the principle may be referred to more generally as the principle of wave propagation, to encompass a wider range of wave phenomena.

Regardless of the specific nomenclature used, Huygen’s principle is a fundamental concept in the study of waves and is essential for understanding the behavior of waves in a variety of settings.

Case Study on Huygen’s principle

One example of the application of Huygen’s principle can be seen in the study of diffraction, which occurs when a wave encounters an obstacle or passes through a narrow aperture. Diffraction is an important phenomenon in wave optics and is used in a variety of applications, such as the design of optical systems and the analysis of crystal structures.

To illustrate the use of Huygen’s principle in the study of diffraction, consider a simple experiment in which a laser beam is passed through a narrow slit and allowed to diffract onto a screen behind the slit. According to Huygen’s principle, each point on the wavefront of the laser beam can be considered as a source of secondary waves that propagate outwards in all directions. The secondary waves interfere with each other to produce a diffraction pattern on the screen.

Using Huygen’s principle, we can predict the shape and intensity of the diffraction pattern. The shape of the pattern will depend on the wavelength of the laser light, the size of the slit, and the distance between the slit and the screen. For a narrow slit, the diffraction pattern will consist of a central bright spot, surrounded by a series of concentric rings of decreasing intensity. The size and spacing of the rings will depend on the parameters of the experiment.

The diffraction pattern can be analyzed using Fourier optics, which is a mathematical technique that allows us to decompose the pattern into its component frequencies. This can be useful for understanding the properties of the diffracted light, such as its spatial frequency and coherence.

Overall, this example illustrates how Huygen’s principle can be applied to the study of diffraction, which is an important phenomenon in wave optics. The principle allows us to predict the behavior of waves as they interact with obstacles and to design systems that take advantage of these properties.

White paper on Huygen’s principle

Introduction

Huygen’s principle is a fundamental concept in the study of wave propagation and is widely used in a variety of fields, including optics, acoustics, and electromagnetism. The principle was first proposed by the Dutch physicist Christiaan Huygens in the 17th century and provides a powerful tool for understanding the behavior of waves in a variety of settings.

Overview of Huygen’s Principle

Huygen’s principle states that every point on a wavefront can be considered as a source of secondary waves or wavelets that propagate outwards in all directions. These secondary waves interfere with each other to produce the overall wave pattern.

The principle can be applied in a variety of contexts, such as the study of diffraction, refraction, and reflection of waves. In each case, the principle allows us to predict the behavior of waves as they encounter obstacles or pass through different media.

Diffraction

One important application of Huygen’s principle is in the study of diffraction, which occurs when a wave encounters an obstacle or passes through a narrow aperture. Diffraction is an important phenomenon in wave optics and is used in a variety of applications, such as the design of optical systems and the analysis of crystal structures.

According to Huygen’s principle, each point on a wavefront can be considered as a source of secondary waves that interfere to produce the overall wave pattern. In the case of diffraction, the wave encounters an obstacle or aperture that causes the secondary waves to interfere in a particular way, producing a diffraction pattern on a screen behind the obstacle.

Refraction

Another important application of Huygen’s principle is in the study of refraction, which occurs when a wave passes from one medium to another with a different refractive index, such as from air to water. According to Huygen’s principle, each point on the wavefront can be considered as a source of secondary waves that propagate outwards in all directions. The secondary waves that reach the boundary between the two media will be refracted, or bent, at an angle that depends on the difference in refractive index between the two media.

Reflection

A third important application of Huygen’s principle is in the study of reflection, which occurs when a wave encounters a reflecting surface, such as a mirror. According to Huygen’s principle, each point on the wavefront can be considered as a source of secondary waves that propagate outwards in all directions. The secondary waves that reach the reflecting surface will be reflected back at an angle that depends on the angle of incidence and the orientation of the surface.

Conclusion

Huygen’s principle provides a powerful tool for understanding the behavior of waves in a variety of settings. The principle allows us to predict the behavior of waves as they encounter obstacles or pass through different media, and it is widely used in the study of optics, acoustics, and electromagnetism. By applying the principles of wave propagation, we can design systems that take advantage of the unique properties of waves and develop new technologies that rely on wave phenomena.